机器学习笔记（6）——线性回归&逻辑回归

机器学习笔记（6）——线性回归&逻辑回归

本文部分图片来源网络或学术论文，文字部分来源网络与学术论文，仅供学习使用，持续修改完善中。

提示：配合西瓜书食用更佳~

目录

机器学习笔记（6）——sklearn实现线性回归&逻辑回归

1、线性回归

西瓜书线性回归代码

 sklearn实现一元线性回归

 sklearn实现多元线性回归

 线性判别分析LDA

2、逻辑回归

损失函数

sklearn实现逻辑回归

鸢尾花数据集做逻辑回归

---

首先，回忆一下分类和回归的区别：预测的变量是连续的是回归任务（线性回归、逻辑回归），预测的变量是离散的是分类任务（决策树，SVM）

处理数据的一个思路
当我们获取数据时，我们往往希望使用线性模型来对数据进行最初的拟合（线性回归用于回归，逻辑回归用于分类）。
如果线性模型表现良好，则说明数据本身很可能是线性的或者线性可分的，
如果线性模型表现糟糕，那毫无疑问我们会投入决策树，随机森林这些模型的怀抱，就不必浪费时间在线性模型上了。

1、线性回归

线性回归：是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

西瓜书线性回归代码

西瓜数据集如下：
1 0.697 0.460 1
2 0.774 0.376 1
3 0.634 0.264 1
4 0.608 0.318 1
5 0.556 0.215 1
6 0.403 0.237 1
7 0.481 0.149 1
8 0.437 0.211 1
9 0.666 0.091 0
10 0.243 0.267 0
11 0.245 0.057 0
12 0.343 0.099 0
13 0.639 0.161 0
14 0.657 0.198 0
15 0.360 0.370 0
16 0.593 0.042 0
17 0.719 0.103 0

import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

def sigmoid(x):  
    """
    Sigmoid函数：将输入值转化为接近0或1的值
    :param x:需要处理的变量（这里多为矩阵）
    :return 经sigmoid函数处理后的值
    """
    return 1.0 / (1 + np.exp(-x))

def getData():
    """
    getData函数：从文件中读取数据，转化为指定的ndarray格式
    :returns  X：样本，格式为：每行一条数据，列表示属性
    :returns  label：对应的标签
    """
    label = []#标签
    density = []#密度
    sugar_rate = []#含糖量
    with open("西瓜数据集.txt",encoding='utf8') as fp:
        file_read = fp.readlines()#读取到的文件内容，一行为一个字符串存储在列表中
    for i in file_read:#由于读取到字符串，现对字符串处理，提取属性以及标签。
        tmp = i.split()#将每一行内容切割
        density.append(eval(tmp[1]))#提取密度信息到列表
        sugar_rate.append(eval(tmp[2]))#提取含糖量信息到列表
        label.append(eval(tmp[3]))#提取瓜的标签信息
        
    '''转化为np格式便于后续处理'''
    sugar_rate = np.array(sugar_rate)
    density = np.array(density)
    label = np.array(label).reshape(len(label),1)
    X = np.vstack((density, sugar_rate)).T#转换成每列代表属性，行代表样本
    return X,label

def calAccuracy(pred,label):
    """
    calAccuracy函数：计算准确率
    :param pred:预测值
    :param label:真实值
    :returns acc：正确率
    :returns p：查准率
    :returns r：查全率
    :returns f1:F1度量
    """
    num = len(pred)#样本个数
    TP = 0
    FN = 0
    FP = 0
    TN = 0
    '''分别计算TP FP FN TN'''
    for i in range(num):
        if pred[i, 0] > 0.5 and label[i]==1:
            TP += 1
        elif pred[i, 0] > 0.5 and label[i]==0:
            FP += 1
        elif pred[i, 0] <= 0.5 and label[i]==1:
            FN += 1
        elif pred[i, 0] <= 0.5 and label[i]==0:
            TN += 1
    '''计算准确率 查准率 查全率 F1度量'''
    acc = (TN+TP) / num
    if TP+FP==0:
        p = 0
    else:
        p = TP/(TP+FP)
    if TP+FN == 0:
        r = 0
    else:
        r = TP/(TP+FN)
    if p+r==0:
        f1 = 0
    else:
        f1 = 2*p*r/(p+r)
    return acc,p,r,f1

def train(train_data,train_label,epoch,lr):
    """
   train函数：训练逻辑斯蒂回归模型
   :param train_data:训练样本
   :param train_label:训练标签
   :param epoch:训练次数
   :param lr:学习率
   :return w:训练最终得到的参数
   """
    w = np.ones((train_data.shape[1]+1,1))#随机初始化参数w，w shape[属性+1,1]
    add_col = np.ones((train_data.shape[0],1))
    x = np.c_[train_data,add_col]#将原始数据增加一列即是x = (个数,属性+1)
    iteration = 0#记录训练次数
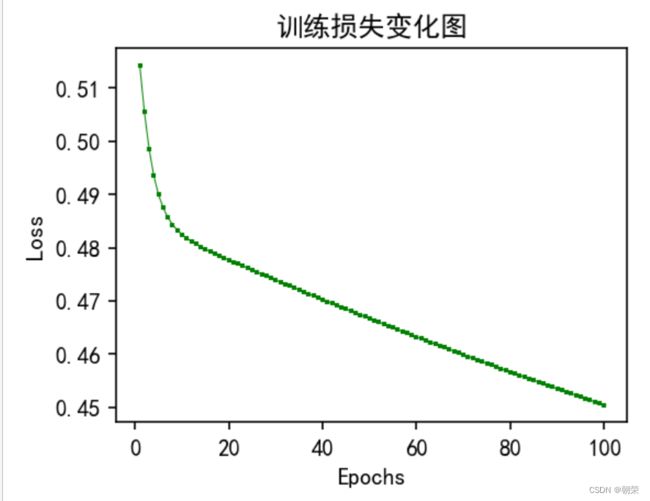
    Loss = []#记录损失值，用来画图
    P = []#记录查准率，用来画图
    R = []#记录查全率，用来画图
    while iteration

def test(test_data,test_label,w):
    """
      train函数：训练逻辑回归模型
      :param test_data:测试样本
      :param test_label:测试标签
      :param w:训练最终得到的参数
      """
    add_col = np.ones((test_data.shape[0], 1))
    x = np.c_[test_data, add_col]  # 将原始数据增加一列即是x = (个数,属性+1)
    pred = sigmoid(np.dot(x, w))  # 计算预测值，预测值要是用sigmoid函数，使其靠近0或者1
    acc,p,r,f1 = calAccuracy(pred, test_label)  # 计算正确率,召回率，查全率，F1度量
    b = pred - test_label  # 实际和预估的差值
    loss = np.average(np.abs(b))
    print("loss值：{:.6f}\t准确率：{:.4f}\t查准率：{:.4f}\t查全率：{:.4f}\tF1度量：{:.4f}".format(loss,acc,p,r,f1))

data,label = getData()
x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.3)#按照训练：测试=7:3比例划分训练集和测试集
w = train(x_train,y_train,1000,0.01) #epoch=500,lr学习率=0.01
test(x_test,y_test,w)
#对比中可以得出，其实模型很不稳定 高低起伏严重

 sklearn实现一元线性回归

#西瓜数据集-sklearn实现线性模型模型
import numpy as np
from sklearn import linear_model  # 表示，可以调用sklearn中的linear_model模块进行线性回归。
import matplotlib.pyplot as plt
print("------------sklearn-----------")
  
data,label = getData()
x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.3)
#print(x_train)
#print(y_train)

model = linear_model.LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)

acc,p,r,f1 = calAccuracy(pred,y_test)
print("准确率：{:.4f}\t查准率：{:.4f}\t查全率：{:.4f}\tF1度量：{:.4f}".format(acc,p,r,f1))

 

#自建数据集，使用sklearn进行线性回归 y=wx+b
import numpy as np
from sklearn.linear_model import LinearRegression # 导入线性回归模型
import matplotlib.pyplot as plt

def true_fun(X):
    return 1.5*X + 0.2

np.random.seed(0) # 随机种子
n_samples = 30
'''生成随机数据作为训练集'''
X_train = np.sort(np.random.rand(n_samples)) 
y_train = (true_fun(X_train) + np.random.randn(n_samples) * 0.05).reshape(n_samples,1)
print(X_train)
print(y_train)
model = LinearRegression() # 定义模型
model.fit(X_train[:,np.newaxis], y_train) # 训练模型

print("输出参数w:",model.coef_) # 输出模型参数w
print("输出参数:b",model.intercept_) # 输出参数b

X_test = np.linspace(0, 1, 100)
plt.figure(figsize=(4,3),dpi=150)
plt.plot(X_test, model.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X_train,y_train) # 画出训练集的点
plt.legend(loc="best")
plt.show()

 sklearn实现多元线性回归

 

#以三元线性回归为例
from sklearn.linear_model import LinearRegression

X_train = [[1,1,1],[1,1,2],[1,2,1],[2,1,1],[1,4,7]]
y_train = [[6],[9],[8],[6],[8]]
 
model = LinearRegression()
model.fit(X_train, y_train)
print("输出参数w:",model.coef_) # 输出参数w1,w2,w3
print("输出参数b:",model.intercept_) # 输出参数b

test_X = [[1,3,5]]
pred_y = model.predict(test_X)
print("预测结果:",pred_y)

#自创数据集进行多元线性回归，最高次分别为1 4 15
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

def true_fun(X):
    return np.cos(1.5 * np.pi * X)
np.random.seed(0)

n_samples = 30
degrees = [1, 4, 15] # 多项式最高次

X = np.sort(np.random.rand(n_samples)) 
y = true_fun(X) + np.random.randn(n_samples) * 0.1

plt.figure(figsize=(14, 5),dpi=150)
for i in range(len(degrees)):
    ax = plt.subplot(1, len(degrees), i + 1)
    plt.setp(ax, xticks=(), yticks=())

    polynomial_features = PolynomialFeatures(degree=degrees[i],
                                             include_bias=False)
    linear_regression = LinearRegression()
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)]) # 使用pipline串联模型
    pipeline.fit(X[:, np.newaxis], y)

    # 使用交叉验证
    scores = cross_val_score(pipeline, X[:, np.newaxis], y,
                             scoring="neg_mean_squared_error", cv=10)
    X_test = np.linspace(0, 1, 100)
    plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
    plt.plot(X_test, true_fun(X_test), label="True function")
    plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
        degrees[i], -scores.mean(), scores.std()))
plt.show()

 线性判别分析LDA

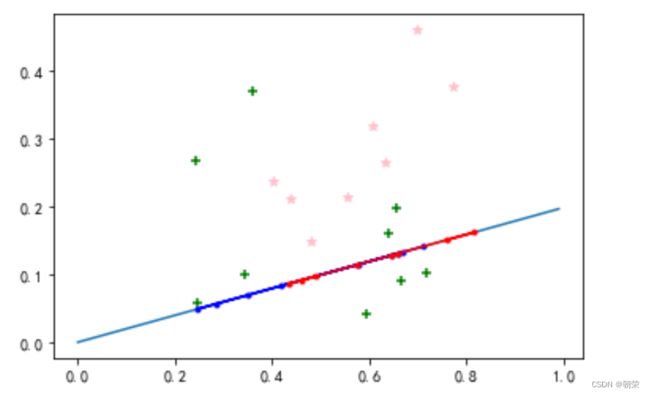
将给定的数据集，投影到一条直线上，使得同类样本投影点尽可能接近，异类样本点尽可能远离。
对于新数据，将其投影到这条直线上，根据投影点的位置确定样本的类别。 

import numpy as np
import matplotlib.pyplot as plt

def getData():
    """
    getData函数：从文件中读取数据，转化为指定的ndarray格式
    :returns  X0：标签为0的样本
    :returns  X1：标签为1的样本
    """
    X0 = []
    X1 = []
    with open("西瓜数据集.txt",encoding='utf8') as fp:
        file_read = fp.readlines()#读取到的文件内容，一行为一个字符串存储在列表中
    for i in file_read:#由于读取到字符串，现对字符串处理，提取属性以及标签。
        tmp = i.split()#将每一行内容切割
        tmp.pop(0)#这一步是除去索引
        tmp_label = eval(tmp.pop(-1))#提取标签
        tmp = [eval(i) for i in tmp]#将字符串转为数字
        if tmp_label==0:#是反例子
            X0.append(tmp)
        else:
            X1.append(tmp)
    '''转化为np格式便于后续处理'''
    X0 = np.array(X0)
    X1 = np.array(X1)
    return X0,X1

def LDA(x0,x1):
    """
    LDA函数：根据接收到两类样本，计算w
    :return  w
    """    
    u0 = np.mean(x0, axis=0)# 求均值
    u1 = np.mean(x1, axis=0)
   
    conv0 = np.dot((x0-u0).T,(x0-u0)) #求协方差矩阵
    conv1 = np.dot((x1 - u1).T, (x1 - u1)) 
    Sw = conv0+conv1 #计算类内散度矩阵
    w = np.dot(np.mat(Sw).I, (u0 - u1).reshape(len(u0), 1))    #由拉格朗日乘法子计算w
    return w

def plot(w,X0,X1):
    """
    plot函数：对结果进行可视化
    :param w
    :param X0,X1:两类样本
    """
    #画直线
    k = w[0]/w[1]
    x_line = np.arange(0, 1,0.01)
    yy = k[0][0] * x_line
    yy = np.ravel(yy)#降维

    #计算反例在直线上的投影点
    xi = []
    yi = []
    for i in range(0, len(X0)):
        y0 = X0[i, 1]
        x0 = X0[i, 0]
        x1 = (k * y0 + x0) / (k ** 2 + 1)
        y1 = k * x1
        xi.append(x1)
        yi.append(y1)
    xi = np.array(xi).reshape(len(xi),1)
    yi = np.array(yi).reshape(len(yi),1)
    # 计算第二类样本在直线上的投影点
    xj = []
    yj = []
    for i in range(0, len(X1)):
        y0 = X1[i, 1]
        x0 = X1[i, 0]
        x1 = (k * y0 + x0) / (k ** 2 + 1)
        y1 = k * x1
        xj.append(x1)
        yj.append(y1)
    xj = np.array(xj).reshape(len(xj), 1)
    yj = np.array(yj).reshape(len(yj), 1)

    plt.figure()
    plt.plot(x_line, yy)
    #绘制初始数据散点图
    plt.scatter(X0[:,0],X0[:,1], marker='+',color='green')
    plt.scatter(X1[:,0],X1[:,1], marker='*',color='pink')
    
    # 画出投影后的点
    plt.plot(xi, yi, marker='.',color='b')
    plt.plot(xj, yj, marker='.',color='r')
    plt.show()


X0,X1 = getData()
w = LDA(X0,X1)
plot(w,X0,X1)

 

2、逻辑回归

对数据的要求程度：线性回归 > 逻辑回归 > 随机森林/决策树

线性回归：对数据的要求很严格，比如标签必须满足正态分布，特征之间的多重共线性需要消除等等，而现实中很多真实情景的数据无法满足这些要求，因此线性回归在很多现实情境的应用效果有限。

逻辑回归：是由线性回归变化而来，因此它对数据也有一些要求，需要预处理。

决策树和随机森林：分类效力很强，就不需要对数据做任何预处理。

逻辑回归与线性回归的不同：

Logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。

逻辑回归的本质，它是一个返回对数几率的，在线性数据上表现优异的分类器。

逻辑回归的自变量和因变量：

自变量	以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的，幽门螺旋杆菌权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
因变量	logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。

据说：福布斯杂志在讨论逻辑回归的优点时，甚至有着“技术上来说，最佳模型的AUC面积低于0.8时，逻辑回归非常明显优于树模型”的说法。并且，逻辑回归在小数据集上表现更好，在大型的数据集上，树模型有着更好的表现。

损失函数

我们使用”损失函数“这个评估指标，来衡量参数为 的模型拟合训练集时产生的信息损失的大小，并以此衡量参数 的优劣。如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。即是说，我们在求解参数 时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

衡量参数 的优劣的评估指标，用来求解最优参数的工具 损失函数小，模型在训练集上表现优异，拟合充分，参数优秀 损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕 我们追求，能够让损失函数最小化的参数组合 注意：没有”求解参数“需求的模型没有损失函数，比如KNN，决策树

正则化
正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量 的L1范式和L2范式的倍数来实现。这个增加的范式，被称为“正则项”，也被称为"惩罚项"。损失函数改变，基于损失函数的最优化来求解的参数取值必然改变，我们以此来调节模型拟合的程度。其中L1范式表现为参数向量中的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。

 L1与L2的区别：

L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小），参数的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。
L1正则化在逐渐加强的过程中，携带信息量小的、对模型贡献不大的特征的参数，会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0，所以L1正则化本质是一个特征选择的过程，掌管了参数的“稀疏性”。L1正则化越强，参数向量中就越多的参数为0，参数就越稀疏，选出来的特征就越少，以此来防止过拟合。因此，如果特征量很大，数据维度很高，我们会倾向于使用L1正则化。由于L1正则化的这个性质，逻辑回归的特征选择可以由Embedded嵌入法来完成。
L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大的特征的参数会非常接近于0。
 

sklearn实现逻辑回归

import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn import model_selection
from sklearn import metrics
def getData():
    """
    getData函数：从文件中读取数据，转化为指定的ndarray格式
    :returns  X：样本，格式为：每行一条数据，列表示属性
    :returns  label：对应的标签
    """
    label = []#标签
    density = []#密度
    sugar_rate = []#含糖量
    with open("西瓜数据集.txt",encoding='utf8') as fp:
        file_read = fp.readlines()#读取到的文件内容，一行为一个字符串存储在列表中
    for i in file_read:#由于读取到字符串，现对字符串处理，提取属性以及标签。
        tmp = i.split()#将每一行内容切割
        density.append(eval(tmp[1]))#提取密度信息到列表
        sugar_rate.append(eval(tmp[2]))#提取含糖量信息到列表
        label.append(eval(tmp[3]))#提取瓜的标签信息
    '''转化为np格式便于后续处理'''
    sugar_rate = np.array(sugar_rate)
    density = np.array(density)
    label = np.array(label).reshape(len(label),1)
    X = np.vstack((density, sugar_rate)).T#转换成每列代表属性，行代表样本
    return X,label

X,y = getData()

density = X[:,0]
ratio_sugar = X[:,1]

print(density)
print(density[:8])
print(density[8:])

# 绘制分类数据
plt.figure()
plt.title('西瓜数据集')
plt.xlabel('density')
plt.ylabel('ratio_sugar')

#绘制散点图（x轴为密度，y轴为含糖率）
plt.scatter(density[:8], ratio_sugar[:8], marker = 'o', color = 'k', s=20, label = 'bad')
plt.scatter(density[8:], ratio_sugar[8:], marker = 'o', color = 'g', s=20, label = 'good')
plt.legend(loc = 'upper right')
plt.show()

#从原始数据中选取0.7数据进行训练，0.3数据进行测试
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.3, random_state=0)
# 逻辑回归模型
log_model = LogisticRegression()
# 训练逻辑回归模型
log_model.fit(X_train, y_train)
# 预测y的值
y_pred = log_model.predict(X_test)
# 查看测试结果
print(metrics.confusion_matrix(y_test, y_pred))

print(metrics.classification_report(y_test, y_pred))

鸢尾花数据集做逻辑回归

#鸢尾花数据集做逻辑回归
from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

iris = datasets.load_iris()

X = iris.data[:, [2, 3]] #取鸢尾花的第2 3列数据，他们分布在0 1 2三个类别
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1000)

# print(X)
# print(y)

## 定义 逻辑回归模型
clf = LogisticRegression()
# 在训练集上训练逻辑回归模型
clf.fit(X_train, y_train)

## 查看其对应的w
print('逻辑回归的权重：\n',clf.coef_)
## 查看其对应的w0
print('逻辑回归的截距(w0):\n',clf.intercept_)

## 因为3分类，所有我们这里得到了三个逻辑回归模型的参数，其三个逻辑回归组合起来即可实现三分类。
## 在训练集和测试集上分别利用训练好的模型进行预测
train_predict = clf.predict(X_train)
test_predict = clf.predict(X_test)

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('逻辑回归准确度:',metrics.accuracy_score(y_train,train_predict))
print('逻辑回归准确度:',metrics.accuracy_score(y_test,test_predict))

## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('混淆矩阵结果：\n',confusion_matrix_result)

x = np.arange(-5,5,0.01)# -5到5 步长为0.01
y = 1/(1+np.exp(-x))#Logistic函数

plt.plot(x,y)#x轴数据和y轴数据
plt.xlabel('x')
plt.ylabel('y')# x,y轴的标签
plt.grid() # 生成网格，便于观察
#plt.savefig("fx.png")# 保存到本地
plt.show()