吴恩达机器学习笔记(四)——多元线性回归
1. 多特征
在之前学的线性回归中,只有一个特征。但是在实际生活中,我们还会考虑许多因素,因此通常会使用到多元线性回归。
在这里,我们依然使用波特兰的房价数据,但是在前面的基础上,增加了多个特征进行房价的预测。具体如下图:

为此我们需要增加一些符号的定义:
n代表特征的个数(上图中n=4)
m代表训练集样本的个数(上图中m=47)
x(i)代表第i个样本(上图中x(2)=[1416,3,2,40])
xj(i)代表第i个样本的第j个特征(上图中x2(2)=3)
为了对上述的公式进行简化,我们首先令x0=1,这样就可以得到一个通用形式,如下图:
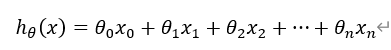
然后,我们将x和θ分别写成向量的形式,如下图:
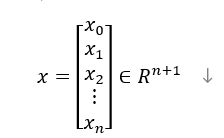
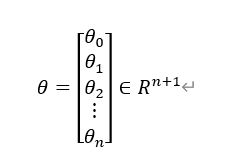
这样,我们可以就可以对公式进行简化,利用线性代数中内积的概念,写成向量相乘的形式,如下图
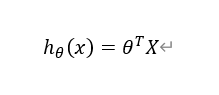
2. 多元梯度下降算法
其实多元梯度下降算法和上一次的笔记中的一元梯度下降算法的原理是一样的。
现规定一个假设函数,如下图:
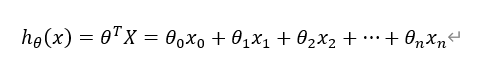
代价函数如下图:
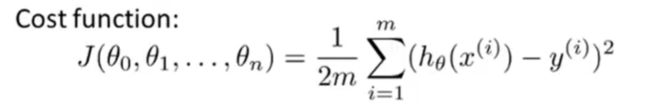
然后不断重复以下过程就可以得到最佳结果(注意需要同步更新),如下图:

下面展示一元和多元在梯度下降方面的对比,可以发现原理其实是完全一样的,如下图:

3. 梯度下降之特征缩放
在进行多元的梯度下降时,如果各个特征的取值范围比较相近,那么梯度下降的收敛速度会比较快。如果各个特征的取值范围差异较大,那么梯度下降的收敛过程就会比较缓慢。
举个例子,下面的例子中包含两个特征,很明显可以看到两个特征的取值范围相差比较大,因此梯度下降就很缓慢。并且由于特征x1的导数会比较大,所以就会呈现一个比较扁的椭圆。可以观察到,梯度下降是很缓慢的。如下图:
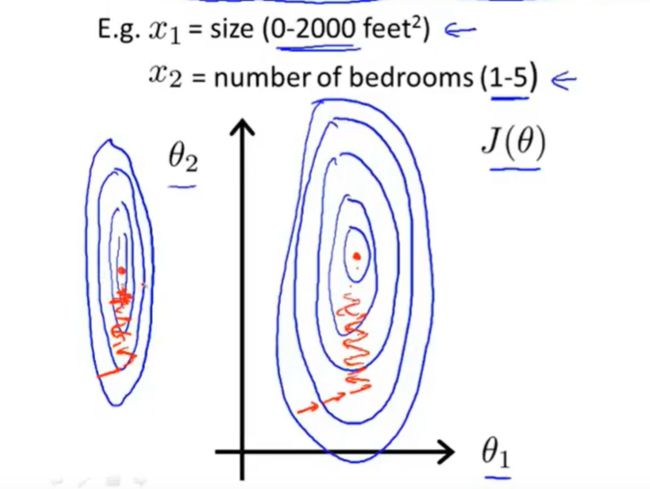
针对这种问题的解决办法通常是对特征进行缩放,通过对特征进行缩放就可以获得一个梯度下降更快的代价函数。如下图:

对于梯度下降,特征的取值范围最好是位于【-1,1】之间。其实在【-1,1】之间也是可以的,但是不能太过于大或者太过于小,如下图:

对于上面的采用数值除以最大值的方法进行缩放,其实还有一些其他的方法。
例如我们有时也会进行一个称为均值归一化的工作,通过均值归一化,可以使得我们进行梯度下降的时候能够收敛的更快。
具体注意点如下:
- 通常会使用特征xi减去该特征的均值ui,也就是xi-ui。这样做的目的是为了让你的特征值具有为0的平均值。
- 对于x0是不需要进行变换的,因为不可能使得具有为0的平均值
- 更一般的规律如下图,Si=当前特征最大值-当前特征最小值,xi代表当前特征的原数值,ui代表当前特征的原数值的平均值。当然Si也可以用当前特征的标准差来代替。

具体实现如下图:

4. 梯度下降之学习率α
学习率α会影响梯度下降的成功与否,因此这里就进一步讨论学习率α如何选取。
我们通常会绘制一幅图来确定我们是否正确运行梯度下降,我们期望得到类似于下图的结果,如下图:
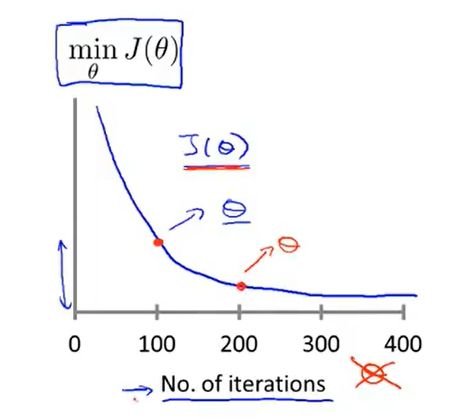
当我们发现J(θ)下降幅度不大的时候,就差不多是收敛了。
当然,我们还可以进行一些自动的收敛测试来判断是否已经收敛,例如判断前后两次迭代的下降值是否小于某个数,如10-3次方等等,但是这个数是比较难以判定的。因此还是画图来得直观。自动收敛测试如下图所示。

接下来讨论几种梯度下降没有正常工作的情况。
最后,数学家已经证明,只要α足够小,那么每次迭代后代价函数都会下降。 但是,我们也不希望α太小,因为这样下降会十分缓慢。
5. 构建新特征和多项式的回归
现在假设我们要对房价进行预测,现有训练集中有房子占地的长度和宽度两个特征。如果利用我们前面学到的知识,我们很容易想到利用这两个特征构建一个二元线性回归来预测房价,如下图:

但是,我们也可以从不同的角度看待这个问题。例如我们可以通过房子的面积来预测房价,我们通过构建一个新的特征area

从而构造一个一元的线性回归进行预测房价,如下图:

对于下面的训练集,很明显不适合使用直线进行拟合,因此我们可以考虑使用二次多项式,三次多项式进行拟合。如下图:

对于多项式的拟合,我们可以利用多元线性回归的方法进行拟合。如下图:
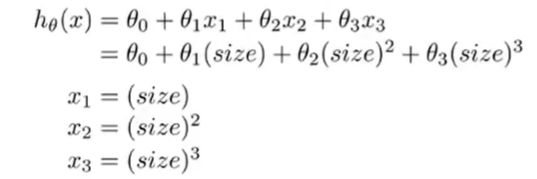
对于这里,我们就会发现特征的缩放就显得尤为重要了,如下图:

6. 正规方程
到目前为止,我们都是一直通过梯度下降算法求解最优的θ,这一小节就会学习另一种求最优θ的方法,也就是正规方程的方法。正规方程的方法无需进行迭代,可以直接求得最优的θ。
现在我们假设代价函数J(θ)如下图:
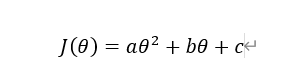
对这个代价函数进行可视化,可以大致描绘出以下图像:
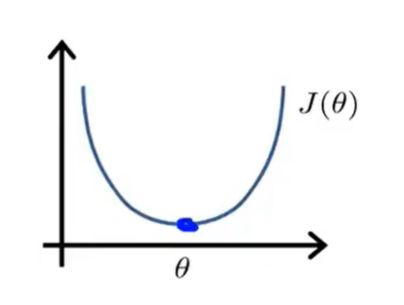
然后我们在学习高数的时候,通常会利用求导的方式求一个函数的极值点,如下图:

我们对其进行推广,拓展到代价函数中,通过计算求偏导,分别令导函数等于0,也可以求得结果,但是明显是比较麻烦的,如下图所示:
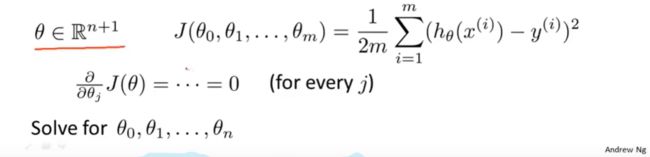
下面具体介绍使用正规方程的方法,我们有如下例子:

首先要做的是在数据集中加上一列,对应额外的特征变量x0,它的取值永远是1。
第二步是将上表中的数据填写到矩阵中,如下图所示:

第三步就是通过计算下列公式,直接求出最优的θ,如下图所示:
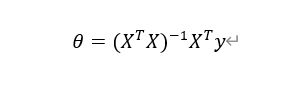
并且对于使用正规方程法求最优θ,是不需要进行特征缩放的,例如下图的特征范围都是可行的:

最后对于梯度下降和正规方程进行对比,主要有以下几个方面:
- 梯度下降的缺点就是需要选择学习率α,并且需要进行多次迭代。而正规方程则可以直接计算得到结果。
- 但是梯度下降法也会存在一些优点,就是对于特征数量n特别大的情况也是能够非常好工作的。
- 而正规方程法在特征数量n很大的情况下,由于要计算(XTX)-1,所以计算量会变得很大,就会工作的非常慢
- 因此,通常如果特征数量n小于10000,那么会选择正规方程,这样计算更加快速。当大于10000时,则通常会使用梯度下降算法。
7. 正规方程不可逆情况
因为使用正规方程的方法计算时,会利用到如下公式:
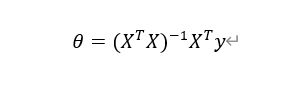
因此,就会涉及到矩阵是否可逆的情况,只有矩阵可逆才可以进行求逆。
那么通常会在什么情况下出现矩阵不可逆的情况呢?