机器学习&数据挖掘笔记_17(PGM练习一:贝叶斯网络基本操作)
前言:
以前在coursera上选过一门PGM的课(概率图模型),今天上去才发现4月份已经开课了,6月份就要结束了,虽然最近没什么时间,挤一点算一点,所以得抓紧时间学下。另外因为报名这些课程的时候,开课老师是不允许将课程资料和code贴在网上的,所以作为学生还是要听从老师的要求,所以这个系列的笔记只是简单的写下,完全留给自己看的,内容估计不会很完整的。
笔记:
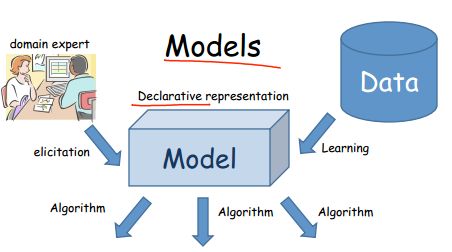
模型的表示其来源可以由相应领域的专家给出,也可以直接从数据中学习到。如下所示:
模型的准确性具有不确定性主要是因为:对现实世界的描述不全面;观察到的数据有噪声;模型只是体现大部分的数据,对某些特例不会考虑;模型固有的不确定性。
PGM模型在实际使用时需要考虑以下几个方面:
表达阶段:有图模型还是无图模型,时序模型还是平面模型。
推理阶段:近似推理还是确定推理,是否需要做出决定。
学习阶段:是学习网络的参数还是连结构也需要学习,是否使用全部数据。
一个factor其实就是一个因果表,因果表中变量组成的集合称为scope。两个factor是可以相乘的,称为factor product. Factor也可以边缘化,即把表中边缘变量给求和积分掉。另外还可以从factor中提取出部分行,这种操作称为factor reduction。还可以根据新获得的evidence来更改factor的概率值。
在PGM模型中使用factor的原因是:在高维空间的数据分布中,factor是一个基本的模块。这些高维空间中的大数据也可以由小的factor相乘组成,并且一些基本的操作都是相通的。
编程作业:
这次实验是熟悉下SamIam这个软件,该软件是专门正对PGM的实际应用开发的,具体介绍和使用参考官网:http://reasoning.cs.ucla.edu/samiam/index.php。首先第一个小题就是构造一个贝叶斯网络图,节点已经给出,并且父子关系已经给出了文字描述,只需连线和给出条件概率表值。网络图如下所示:
一些matlab函数:
[C,ia,ib] = intersect(A,B):
返回矩阵C为矩阵A和B中公共的元素,且ia和ib分别为其索引,比如说C=A(ia) 且 C = B(ib)。
B = any(A):
判断A中是否有非零值,默认情况下是对第一维中的元素采用逻辑"AND"操作,所以当A为二维矩阵时,B为一个行向量。
B = all(A):
判断A中是否所有元素值都非零。
C = union(A,B):
C为A和B的并集。
[Lia,Locb] = ismember(A,B):
判断A中元素是否为B中的子元素,如果都不是,则Lia和Locb中元素值都为0(注意,Lia大小和A一样,Locb大小和B一样)。如果A中有元素是B中的,在Lia中对应返回值相应位置为1,而Locb中返回其在B中对应的位置。
B = prod(A):
B表示求A中对应列的元素值的乘积,所以如果A为2维矩阵,则B为行向量。
[C,ia] = setdiff(A,B):
返回的C元素为在A中出现,但是没有在B中出现,ia为其索引值,满足C = A(ia)。
B = cumprod(A):
B和A的尺寸一样。如果A是一个向量,则B中每个元素是A中元素的累积表示。如果A是一个矩阵,则是对A的每一列按照累积乘积表示。
作业中的一些函数:
C = FactorProduct(A, B)
其中A和B为2个factor,C为这2个factor的乘积。
B = FactorMarginalization(A, V):
其中A为一个factor,V为A中的某一些变量(进行边缘化用的),B为A中关于该变量的边缘求和(B表格尺寸变小),所以结果B中不再出现变量V中的元素了。
F = ObserveEvidence(F, E):
F为一个factor的容器。E为一个2列的矩阵,每1行代表1对观察值,其中第1个元素为变量名称v,第2个元素为该变量对应的值,假设为x。作用是在F的每个factor中,只保留变量v等于x时对应assignment的值,而变量v等于其它值的assignment值都清0。但不改变每个factor表格的大小,只是有很多0值的行而已。
Joint = ComputeJointDistribution(F):
F为一个factor的容器,Joint为F中各个factor的乘积。
M = ComputeMarginal(V, F, E):
其中V为需要进行边缘换的变量,F为一个factor的容器,E和上面的解释一样,为观察值对。M为首先通过evidence来更改F中factor的值,然后利用函数数FactorMarginalization根据V来求边缘化的factor,最后需要将这些factor的概率值归一化。
C=IndexToAssignment(I, D):
该函数是将下标I按照向量D的形式转换成一个带下标的矩阵A,说白了就是把I中的每个值按照D中的进位转换。比如I为:
I =
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
D为:[2 3 4]
则C结果为:
1 1 1
2 1 1
1 2 1
2 2 1
1 3 1
2 3 1
1 1 2
2 1 2
1 2 2
2 2 2
1 3 2
2 3 2
1 1 3
2 1 3
1 2 3
2 2 3
1 3 3
2 3 3
1 1 4
2 1 4
1 2 4
2 2 4
1 3 4
2 3 4
I = AssignmentToIndex(A, D):
和上面的那个函数是相反的,这里将A中的每个进位表示按照D中的进位还原成实数。如果A中有值重复,则得到I中对应位置也重复。
总结:
不得不佩服这些公开课,弄得实在太好了,连上交作业都用程序写好了。向这些无私奉献的科研团队致敬!
1. 在用submit进行提交作业时,需要输入邮箱和密码,密码为课程主页自动生成的。这样就会在目录下生成一个登陆作业服务器相关的文件:228_login_data.mat.
2. 求2个factor的乘积时,至少要保证2个factor的scope有交集。
3. 一个factor结构分为3个部分:.var(表示这个factor所含有的变量); .card(表示每个变量所对应的进位,因为前面的var中每个元素代表数中的每一位,而每一位又对应着不同的进位制); .val(表示这个factor可取的元素值,其实只是个标号,没有具
体的数值意义,因此一般用于集合运算,不用于数值运算)。
4. 当已知了一个factor容器中各个factor的值,则可以算出针对这个容器的联合概率(没归一化前,直接将容器中所有factor相乘)。
参考资料:
http://reasoning.cs.ucla.edu/samiam/index.php