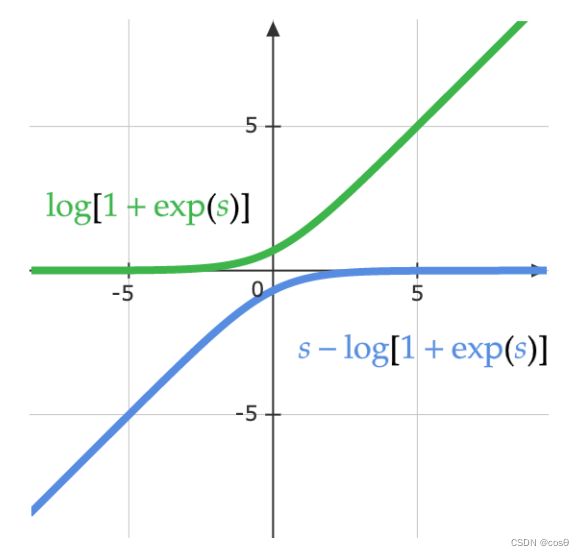纽约大学深度学习PyTorch课程笔记(自用)Week1&2
纽约大学深度学习PyTorch课程笔记Week1&2
- 0. 课程纲要
- 1. Week1
-
- 1.1 深度学习的动机及其历史和启示
-
- 1.1.1 深度学习的灵感和历史
-
- 监督学习
- 1.1.2 模式识别的历史和梯度下降简介
-
- 通过反向传播计算梯度
- 1.1.3 视觉皮层的层次结构
- 1.2 卷积神经网络(CNN)的演化及其用途,为何出现深度学习?
-
- 1.2.1 卷积神经网络(CNN)的演化
- 1.2.2 深度学习和特征提取
- 1.2.3 学习表征
- 1.3 问题动机、线性代数与视觉化
-
- 1.3.1 变换与其动机
- 1.3.2 资料视觉化 - 通过神经网路将不同颜色的点分离
-
- 网络结构
- 1.3.3 随机投影 - Jupyter Notebook
- 2. Week2
-
- 2.1 梯度下降和反向传播算法导论
-
- 2.1.1 梯度下降优化算法
-
- 参数化模型
- 梯度下降
- 2.1.2 在传统神经网络中随机梯度下降和反向传播算法的优势
-
- 随机梯度下降的优势
- 传统神经网络
- 通过非线性函数进行反向传播
- 通过加权和进行反向传播
- 2.1.3 一个神经网络和反向传播的PyTorch实现
-
- 一个传统神经网络的方块图表示
- PyTorch实现
- 对于一个模块进行反向传播
- 对于多层结构的反向传播
- 2.2 为神经网络的模组计算梯度,与反向传播的实用技巧
-
- 2.2.1 一个反向传播的具体例子还有介绍基础的神经网络模组
-
- 范例
- 基本的神经网络模组
- 2.2.2 LogSoftMax vs SoftMax
- 2.2.3 反向传播的实用技巧
-
- 用 ReLU 作为非线性函数
- 用交叉熵作为分类问题的损失函数
- 训练时使用小批量(minibatch)的随机梯度下降
- 训练时打乱样本顺序
- 将输入归一化使其具有零平均值与单位方差
- 按照进度递减学习率
- 使用 L1 和(或)L2 正则化进行权重衰减
- 权重初始化
- 使用 dropout
- 2.3 人工神经网络(ANNs)
-
- 2.3.1 进行分类的监督学习
- 2.3.2 训练数据
- 2.3.3全连接层(fully connected (FC) layer)
- 2.3.4 神经网络(推断 (inference))
- 2.3.5 神经网络(训练 I)
- 2.3.6 神经网络 (训练 II)
0. 课程纲要
- 监督学习,神经网络,和深度学习基础
- 反向传播算法和架构组成
- 卷积神经网络和应用
- 更多深度学习架构
- 正则化技巧/优化技巧/理解深度学习如何工作
- 基于能量的模型 (Energy-based models)
- 自监督学习与更多

1. Week1
1.1 深度学习的动机及其历史和启示
1.1.1 深度学习的灵感和历史
深度学习的概念受到了大脑的启发,但并非大脑的每个细节都重要。类比而言,飞行器的构想受到鸟的启发。它们飞行的原理相同,细节上却截然不同。
深度学习的历史可以追溯到今天我们称为控制论(cybernetics)的学科。20世纪40年代,McCulloch和Pitts萌生出一种想法:神经元是可以开关的阈值单元,可以将神经元联结构成布尔电路并用它进行逻辑推理。因为神经元是二元的,大脑实际上就是个逻辑推理机器。神经元计算出输入的加权和,并与阈值比较。如果结果超出阈值就开启,反之关闭。这便是神经网络工作方式的简单描述。几十年来,相关领域一直采用这个模型。
1947年,Donald Hebb想到大脑中的神经元通过修改彼此间连接(突触)的强度来学习。这叫Hebb学习:当两个神经元一起激发时,它们之间的连接变强;当它们不一起激发时,它们之间的连接变弱。
此后在1948年,Norbert Wiener提出控制论,即通过传感器(sensor)和执行器(actuator),可以构造反馈回路和自调整系统。举例来说,汽车(转向控制)中反馈机制的相关规则和稳定性都源自控制论。
1957年,Frank Rosenblatt提出了感知器。这种算法能修改简单神经网络的权重来学习。
总而言之,通过模拟大量神经元来制造智能机器的想法诞生于20世纪40年代,流行于50年代,而没落于60年代。它没落的根源在于:
研究者们使用的神经元都是二元的。然而只有连续的激活函数才能让反向传播算法发挥作用。当时的研究者们没想到可以用连续的神经元。他们也没想到可以用梯度来训练,因为二元神经元无法微分。
即使有连续的神经元,需要将它的输入与权重相乘才能得到其对权重和的贡献。1980年前,对两个数字,特别是浮点数,进行乘法的过程十分缓慢。这也使得研究者们不愿使用连续神经元。
深度学习于1985年随着反向传播算法的出现再度流行。1995年,该方向再次没落,机器学习社区也舍弃了神经网络的思路。2010年初,人们将神经网络用于语音识别并取得了巨大进展,并将之大量商用。2013年,计算机视觉转向使用神经网路。2016年,自然语言处理亦然。不久,我们将在机器人学、控制学和其它学科中也看到类似的革命。
监督学习
90%的深度学习应用使用监督学习。监督学习中,你需要收集一组对应的输入与输出数据,之后将输入交给机器,令其学习正确的输出。当输出正确时,你不需做任何事情。若输出错误,你修改机器的参数以使输出更接近想要的正确结果。这里的微妙之处是想明白该往哪个方向调整参数以及调整多少。而这就要用到梯度计算和反向传播算法。
监督学习可以回溯到感知机和自适应线型单元(Adaline, Adaptive Linear Element)。Adaline与感知机基于相同的架构,对输入进行加权求和。加权之和高于阈值时开启,低于阈值时关闭。感知机是一种两层神经网络,第二层可训练而第一层固定。大多数情况下,第一层的权重是随机决定的,被称为联想层(associative layer)。
1.1.2 模式识别的历史和梯度下降简介
前述部分构成了深度学习出现之前模式识别的基础。模式识别的基本模型包括特征提取器和可训练分类器。特征提取器从输入数据经中获得有用的特征,比如人脸识别中的任务中检测出眼睛。然后,可训练分类器计算出代表特征的向量的加权和,并与阈值比较。可训练分类器可以是感知机或者一个神经网络。问题是,特征提取器必须由人工设计。因此,模式识别/机器视觉的侧重点变成了为具体问题设计特征提取器,而非可训练分类器。
随着深度学习的出现与发展,这个二阶过程转变为一系列模块。每个模块都包含可微调的参数与非线性单元。我们将它们层层叠起。有multiple layer,因此称之为“深度学习”。我们之所以使用非线性单元而不是线性,是因为两层线型单元的组成仍为线性,因此相当于一层线型单元。
最简单的含可调参数与非线性单元的多层结构是:用向量表现的输入,比如图像或语音。该输入和权重矩阵相乘,矩阵的系数是可调参数。接着,相乘结果的每个部分都通过一个非线性单元,比如ReLU。重复这个过程便得到一个基本的神经网络。它之所以被称为神经网络,是因为这个结构将输入的每个组成部分与矩阵对应的行相乘,获得一个加权和。
回到监督学习的概念上,我们将输出结果与目标输出比较,并优化一个目标函数。这个目标函数,或者说损失,计算结果与目标间的距离/惩罚/差异,并取它在训练集上的平均数。这就是我们要减少的目标。换言之,我们想找到能减少这个平均数的参数值。
我们通过计算梯度的方式来寻找它。举个例子,一个大雾弥漫的夜晚,我们在一座光滑的山上迷路了。我们想下到山谷的村庄里。这时我们可以转身寻找最陡的方向并迈一小步。这个方向就是梯度的反方向。只要假设山谷是凸的,那我们这样重复下去必定能达到山底。
随机梯度下降(stochastic gradient descent)是一种更高效的方法。既然我们想减少整个训练集的平均损失,那每次取一个样本或一小组样本,计算它们的误差并使用梯度下降。接下来取一个新样本并得到一个新的误差,然后算出一个新的梯度。使用随机梯度下降的两个原因:一是经验上当数据集非常大时SGD收敛得更快,二是能取得更好的泛化能力,在其它的数据集上预测时能得到相近的性能。
通过反向传播计算梯度
通过反向传播计算梯度是链式法则的实际应用。
状态梯度的反向传播(计算)如下:
∂ C ∂ x i − 1 = ∂ C ∂ x i ∂ x i ∂ x i − 1 ∂ C ∂ x i − 1 = ∂ C ∂ x i ∂ f i ( x i − 1 , w i ) ∂ x i − 1 \begin{aligned} \frac{\partial C}{\partial \boldsymbol{x}_{i - 1}} &= \frac{\partial C}{\partial \boldsymbol{x}_i}\frac{\partial \boldsymbol{x}_i}{\partial \boldsymbol{x}_{i - 1}} \\ \frac{\partial C}{\partial \boldsymbol{x}_{i - 1}} &= \frac{\partial C}{\partial \boldsymbol{x}_i}\frac{\partial f_i(\boldsymbol{x}_{i - 1}, \boldsymbol{w}_i)}{\partial \boldsymbol{x}_{i - 1}} \end{aligned} ∂xi−1∂C∂xi−1∂C=∂xi∂C∂xi−1∂xi=∂xi∂C∂xi−1∂fi(xi−1,wi)
权重梯度的反向传播(计算)如下:
∂ C ∂ w i = ∂ C ∂ x i ∂ x i ∂ w i ∂ C ∂ w i = ∂ C ∂ x i ∂ f i ( x i − 1 , w i ) ∂ w i \begin{aligned} \frac{\partial C}{\partial \boldsymbol{w}_{i}} &= \frac{\partial C}{\partial \boldsymbol{x}_i}\frac{\partial \boldsymbol{x}_i}{\partial \boldsymbol{w}_{i}} \\ \frac{\partial C}{\partial \boldsymbol{w}_{i}} &= \frac{\partial C}{\partial \boldsymbol{x}_i}\frac{\partial f_i(\boldsymbol{x}_{i - 1}, \boldsymbol{w}_i)}{\partial \boldsymbol{w}_{i}} \end{aligned} ∂wi∂C∂wi∂C=∂xi∂C∂wi∂xi=∂xi∂C∂wi∂fi(xi−1,wi)
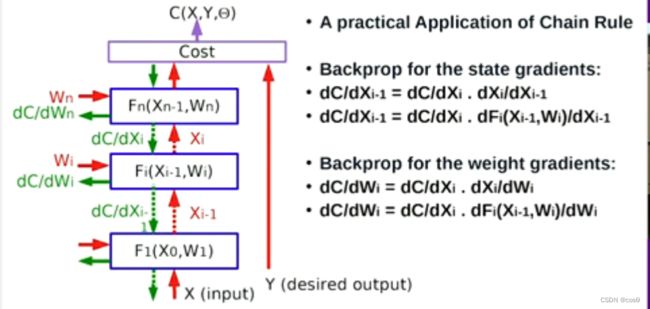
需要注意的是,输入时需要向量而非标量,而且通常是多维向量。反向传播使得我们可以计算真实值与实际输出(目标函数)之差对于网络中任何值的导数。最后,反向传播之所以如此重要是因为它会被应用于多层之上。
考虑如何处理输入十分重要。比如 256 × 256 256\times256 256×256大小的图像需要有 200,000 个值的矩阵。 这些巨型矩阵之后会交给神经网络层来处理,而利用这样的矩阵是不切实际的。因此,对矩阵的结构进行假设十分重要。
1.1.3 视觉皮层的层次结构
福岛邦彦的实验使我们对大脑如何处理视觉有所了解。总的来说,我们发现视网膜前面的神经元压缩了输入(又称对比度归一化),之后视觉信号从我们的眼睛传播到我们的大脑。此后视觉信号被分阶段处理,特定类别的特定神经元被激活。因此,视觉皮层以分层方式进行模式识别。
研究人员在视觉皮层的特定区域(特别是V1区域)的电极实验使他们意识到,某些神经元会对出现在视野中的小区域的图案产生反应,并且临近的神经元对相邻区域也有类似的表现。另外,对同一视野做出反应的神经元会以有组织的方式对不同类型的边缘(垂直或水平边缘)做出反应。 还有一种值得关注的观点是是视觉过程本质上是前馈过程,因此可以在无反复连接的情况下完成快速识别。
1.2 卷积神经网络(CNN)的演化及其用途,为何出现深度学习?
1.2.1 卷积神经网络(CNN)的演化
在动物的大脑中,神经元对特定方向的边缘信息有所反应。对同一方向起反应的神经元群将复制遍整个视野。
Fukushima (1982)基于两个概念构建了一个与大脑工作方式相同的神经网络(NN)。第一,神经元将跨越视野进行复制。 第二,复杂细胞可以将来自简单细胞(方向选择性单元)的信息进行汇合。 这造成的结果就是,图片的移动将改变单个细胞的激活,但是并不影响复杂细胞的集成激活(卷积汇合操作)。
LeCun (1990)使用反向传播算法训练CNN,进行手写数字的识别。在1992年的一个演示中,展示了该算法可以识别任意样式的数字。在那时,使用通过端到端训练的模型进行字符/模式识别非常新颖。在这之前,大家的方案通常是利用 特征提取器再加上一个监督模型。
这些新颖的CNN系统能够同时在图片上识别多个字符。为了实现识别,人们在CNN中使用一个小型的输入窗,并将其滑过整个图像。如果它被激活,那就意味着存在某个特定的字符。
之后,这个想法被应用于面部/人物检测和语义分割(逐像素分类)。包括像Hadsell (2009)和Farabet (2012)这样 的例子。最终,CNN在工业界变得非常普遍,在如车道跟踪这样的自动驾驶应用中也被使用。
在20世纪80年代,用来训练CNN的特殊硬件是一个非常热门的主题。接着,人们对此的兴趣衰退。而如今这个主题则再次变得炙手可热。
深度学习(虽然在那时大家还没有使用这个词)的革命始于2010-2013年。研究人员致力于创造那些可以帮助大型CNN训练变得更加快速的算法。 Krizhevsky (2012)在2012年提出AlexNet。这是一个比以往大得多的卷积神经网络,使用GPU在 ImageNet(130多万张图片)上进行训练。在经过几周的训练之后,AlexNet大幅度超越当时的最佳性能 – 将top-5错误率从25.8%降到16.4%。
在看到AlexNet的成功之后,计算机视觉社区开始确信CNN的有效。虽然2011-2012涉及CNN的论文都被拒稿, 但是自2016以来,大多数被接收的CV论文都使用了CNN。
多年以来,CNN中的层的数量在不断增加:LeNet – 7层,AlexNet – 12层,VGG – 19层,ResNet – 50层。尽管如此,在计算输出的所需操作数、模型的大小和它的准确率之间始终存在着一种权衡。因此当前一个非常热门的主题就是如何压缩网络,使得计算更加快速。
1.2.2 深度学习和特征提取
多层网络之所以成功,是因为它发掘了天然数据的复合结构。在复合的层级结构中,层级中某一层的目标的组合形成 下一层中的目标。如果我们将这个层级结构看做一个多层结构的网络,并且让网络学习特征的合适的组合,那么 我们就得到了所谓的深度学习架构。因此,深度学习网络本质上就是层次化的。
深度学习架构使计算机视觉任务取得了难以置信的发展。从识别并生成围绕目标的准确遮罩(mask)到识别 目标的空间性质。Mask-RCNN和RetinaNet架构对这类改善作出了主要贡献。
Mask RCNN在分割独立目标中被广泛使用。即为图像中的每一个目标建立遮罩。在这个任务中,输入和输出都是图像。该架构还可以被用来执行实例分割任务,即,在一张图像中识别同一类型的不同目标。由Facebook AI 研究院 (FAIR)开发的软件系统:Detectron,实现了所有这些SOTA(state-of-the-art)的目标检测算法并且将其开源。
一些CNN的实际应用还包括赋能自动驾驶和分析医学影像。
虽然人们对深度学习背后的科学和数学已经有了不错的理解,但是仍有一些有趣的问题需要更深入的研究。 这些问题包括:已知我们可以使用两层结构近似任意函数,为什么多层架构会表现的更好?为何CNN在语音、图像、文本这样的天然数据上效果很好?我们如何对非凸函数较好地优化?为什么过度参数化的结构也会有效?
特征提取由扩展表征维度组成,比如扩展的特征更有可能线性可分;由于可能的分离平面数量的增加,使得高维空间 的数据点更有可能线性可分。
早前的机器学习从业者依靠高质量、手工提取、针对特定任务的特征来构建人工智能模型,但是随着深度学习的出现, 模型能够自动提取通用特征。在特征提取算法中的一些常见方法如下:
- 空间贴片
- 随机投影
- 多项式分类器(特征向量积)
- 径向基函数
- 核机
由于数据的复合性质,学到的特征随着抽象层次的增加具有层级化的表征。比如:
-
图像 - 在最细的粒度级别,图像可以被认为是像素。像素的组合构成边缘,边缘的组合构成纹理基元(多边缘形状),纹理基元构成图案,图案构成部分图像。将这些部分图像组合,构成最终的图像。
-
文本 - 类似地,在文本数据中也存在固有的层级。字符形成词,而词形成词组,然后是子句,再然后,将子句合并,我们得到句子。而最终句子会告诉我们故事表达了什么。
-
语音 - 在语音里,样本组成波段,波段组成声音,声音组成元音,继而组成音素,接着是整个词,然后是句子, 这里也同样展现出了清晰的层级化表征。
1.2.3 学习表征
有一种驳斥深度学习的说法:如果我们能够使用2层结构近似任意函数,为何还要更多层?
举个例子:支持向量机(SVM)“从数据中”找到一个分类超平面,这意味着预测是基于训练数据的比较。SVM本质上是一个极简的2层神经网络,其中第一层定义了一个“模板”,第二层则是一个线性分类器。而2层说法的谬误在于,复杂度和中间层的大小是N的指数级(为了完成一个困难的任务,我们需要大量的模板)。但是如果你扩展层的数量到log(N), 那么层的复杂度将成为N的线性级别。这里就存在时间和空间的权衡。
这里再举一个类比:设计一个电路,使用不多于两层的逻辑门来计算一个布尔函数 - 用这种方法,我们其实可以计算任意布尔函数!但是,对于复杂函数而言,第一层(逻辑门的数量)的复杂度和资源将会很快变得无法实现。
什么是“深度”?
- SVM不是深度的,因为它仅仅有两层
- 分类树也不是深度的,因为它的每一层分析了同样的(原始)特征
- 深度网络具有很多层,并且被用来构建一个复杂性递增的特征的层级结构
模型如何学习表征(好的特征)?
流形假设(Manifold Hypothesis):天然的数据存在于一个低维流形上。可能的图像的集合本质上是无限的,而“天然”的图像的集合是其中 一个小子集。比如:对于一个人物的图像,可能的图像的集合规模大约在能移动的面部肌肉的数量(自由度)这个量级 ~(about) 50。一个理想的(同时不切实际的)特征提取器需要表达所有这些变化的因素(每个肌肉、光照、等等等等)。
Manifold
讲稿最后的Q&A:
对于人脸的那个例子,能不能用一些其他的维度约化技术(比如主成分分析(PCA))来抽取这些特征?
回答:只有当流形表面为超平面时可行,但显然这里不是
1.3 问题动机、线性代数与视觉化
1.3.1 变换与其动机
让我们看看一个图像分类的例子。比方我们用一个一百万像素的相机拍一张照片,这张图片铅直、水平各有约 1000 个像素,而每个像素会有红绿蓝三个色彩的维度。每个图像因此就可以当作三百万维空间中的一点。在这样大的维度中,许多我们想分类的有趣图像——像是狗对上猫——必然会在空间中的相同区域中。
为了有效分离这谢图像,我们考虑对资料进行一些变换以移动这些资料点。请回想一下,在二维空间中,一个线性变换等同于矩阵乘法。例如下列这些线性变换:
- 旋转(当矩阵为正交矩阵)
- 缩放(当矩阵为对角矩阵)
- 反射(当行列式为负值)
- 错切
值得注意的是,平移不是一个线性变换,因为原点不会保留在原处,但它是仿射变换。再回到我们的图像例子,我们可以先平移使各点移动到 0 的周遭,再用对角矩阵缩放来放大那个区域,最后,我们就能寻找能分割空间将各点分到各自的类别的直线。亦即,藉由线性与非线性的转换,将资料点映射到一个使他们线性可分的空间。下个部份我们会更具体的说明这个想法。
1.3.2 资料视觉化 - 通过神经网路将不同颜色的点分离
我们的视觉化展现的是由五个股组成的螺旋,每个股对应不同颜色。这些点在一个二维平面中,可以用元组来代表;这些颜色代表第三个维度,或者当作是各点的类别。接着我们可以用一个网路来分开不同颜色的点。
这个网路会拉伸空间以使各点能被分离. 当收敛时,网路会把每种颜色分开至最终流形中的不同子空间。也就是说,新的空间中的每个颜色,对于一对全的回归都是线性可分的。图中的这些向量可以用一个 5 x 2 的矩阵表示;这个矩阵乘上每个点产出属于五种不同颜色的分数,于是每个点可以再以它们的分数分为不同颜色。这里输出维度是五,每个颜色有一个;输入维度则是二,对应 x 与 y 坐标。总之,这个网路对空间进行变换,而这种变换可参数化为数个矩阵与非线性变换。
网络结构
第一个矩阵将 2 维的输入映射到 100 维的隐藏层。接着加上一个非线性层:ReLU,即 Rectified Linear Unit,就是一个输出输入大于零部分的函数 ( ⋅ ) + (\cdot)^+ (⋅)+ 。接下来,为了用图片的方式显示图像,我们用一个嵌入层来将 100 维的隐藏层映射到 2 维的输出。最后,嵌入层被投影到 5 维的最后一层,每个维度代表各个颜色的分数。
1.3.3 随机投影 - Jupyter Notebook
演示代码
2. Week2
2.1 梯度下降和反向传播算法导论
2.1.1 梯度下降优化算法
参数化模型
参数化模型
y ˉ = G ( x , w ) \bar{y} = G(x,w) yˉ=G(x,w)
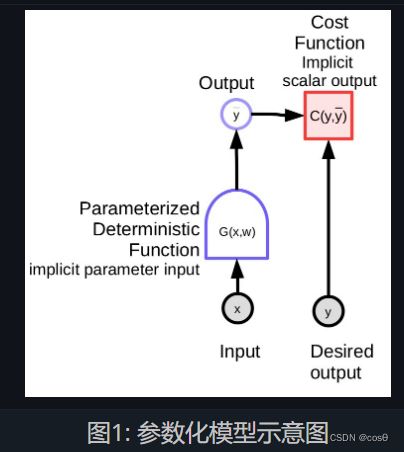
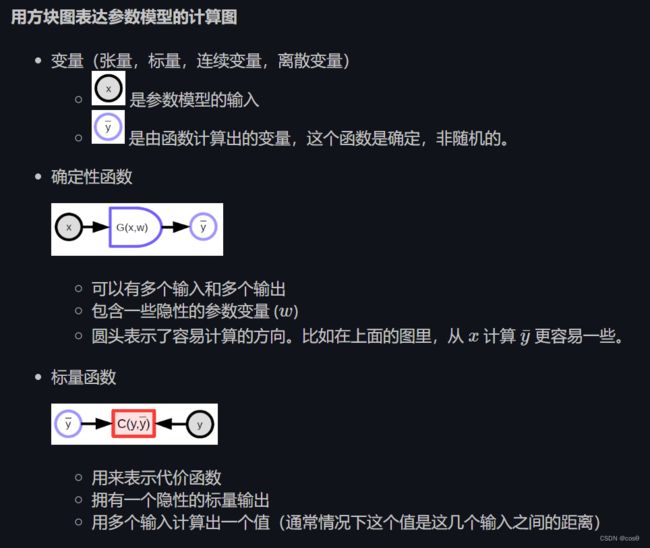
简单来讲,参数化模型就是依赖于输入和可训练参数的函数。 其中,可训练参数在不同训练样本中是共享的,而输入则因每个样本不同而不同。 在大多数深度学习框架中,参数是隐性的:当函数被调用时,参数不被传递。 如果把模型比作面向对象编程,这些参数相当于被“储存在函数中”。
参数化模型(上文提到的函数)包含一个参数向量,这个模型可以将一个输入转化成输出。 在监督学习中,我们把模型的输出 ( y ˉ ) (\bar{y}) (yˉ)送入代价函数 ( C ( y , y ˉ ) ) (C(y,\bar{y} )) (C(y,yˉ)),并将它与正确答案 ( y ) ({y}) (y) 对比。 图1是这个过程的示意图。
- 线性模型 - 输入向量的加权和:
y ˉ = ∑ i w i x i , C ( y , y ˉ ) = ∥ y − y ˉ ∥ 2 \bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2 yˉ=i∑wixi,C(y,yˉ)=∥y−yˉ∥2
- 近邻算法 - 给定一个输入 x 和一个权重矩阵 W,我们用 k 来表示 W 中的某一行。这个模型的输出是矩阵 W 中,与 x 最接近的那一行的编号 k。
y ˉ = arg min k ∥ x − w k , . ∥ 2 \bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2 yˉ=kargmin∥x−wk,.∥2
复杂的函数也可以被用到参数化模型中。
损失函数
在训练过程中,我们最小化损失函数。 大体上存在两种损失函数:
-
逐样本损失函数 - L ( x , y , w ) = C ( y , G ( x , w ) ) L(x,y,w) = C(y, G(x,w)) L(x,y,w)=C(y,G(x,w))
-
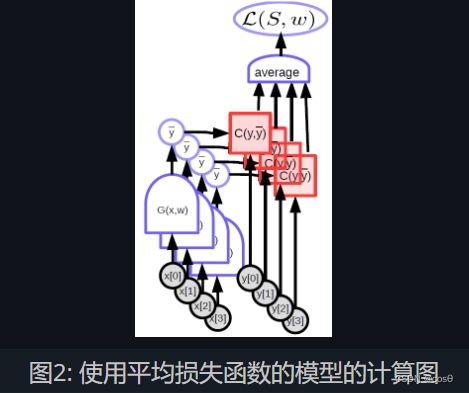
平均损失函数 - 对于任意一个样本的集合 S = { ( x [ p ] , y [ p ] ) ∣ p ∈ { 0 , ⋯ , P − 1 } } S = \lbrace(x[p],y[p]) \mid p \in \lbrace 0, \cdots, P-1 \rbrace \rbrace S={(x[p],y[p])∣p∈{0,⋯,P−1}},
在集合 SS 上的平均损失函数定义为: L ( S , w ) = 1 P ∑ ( x , y ) L ( x , y , w ) = 1 P ∑ P = 0 P − 1 L ( x [ p ] , y [ p ] , w ) L(S,w) = \frac{1}{P} \sum_{(x,y)}L(x,y,w) = \frac{1}{P} \sum_{P=0}^{P-1}L(x[p],y[p],w) L(S,w)=P1∑(x,y)L(x,y,w)=P1∑P=0P−1L(x[p],y[p],w)
在标准的监督学习里,(逐样本)损失函数就是代价函数的输出。 机器学习在很大程度上就是寻找函数的最优解(经常情况下,是寻找某个函数的最小值)。 有的时候(比如在生成对抗网络里),我们学习寻找两个函数的纳什均衡。 我们用一系列和梯度相关的方法(包含但不总是梯度下降)寻找函数的最优解。
梯度下降
假设我们可以很容易地计算一个函数的梯度,我们可以用 梯度相关方法 去寻找这个函数的最小值。 这个方法建立在一个假设上,即,这个函数在大部分区间连续可微分(并不需要在所有地方连续可微分)。
梯度下降背后的逻辑直觉 - 想象在一个大雾弥漫的夜晚,我们在一座山里,想要回到山下的村庄。 因为视野非常有限,我们只能靠观察路面倾斜的角度来判断下山的方向,并且向着那个方向前进。
不同梯度下降的方法:
-
对整批样本进行梯度下降时的参数更新法则: w ← w − η ∂ L ( S , w ) ∂ w w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w} w←w−η∂w∂L(S,w)
-
SGD (随机梯度下降)的参数更新法则:从 { 0 , ⋯ , P − 1 } \lbrace 0, \cdots, P-1 \rbrace {0,⋯,P−1}里选取一个 p p p ,进行参数 w w w的更新
w ← w − η ∂ L ( x [ p ] , y [ p ] , w ) ∂ w w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w} w←w−η∂w∂L(x[p],y[p],w)
SDG利用了样本的冗余:
- 在大多数情况下运行的比全样本梯度下降更快
- 在实际中,我们使用minibatch来进行并行
其中, w {w} w 表示要进行优化的参数。
在这里, η \eta η 是一个常数,但是在更高级的算法中,它可以是一个矩阵。如果这是一个半正定矩阵,虽然我们确实是在往山下走,但是我们走的方向并不一定是向着最陡的方向走。 事实上,最陡的那个方向并不一定总是我们想要去的方向。
如果我们处理的函数不可微分,比如,函数曲线上有个洞,曲线是阶梯形状,或者干脆是平的,这时候梯度不能提供任何有用信息,我们必须借助其他方法 - 比如0阶方法,或者一些不需要梯度计算的方法。 深度学习说白了就是围绕着梯度相关方法展开的。
其实也存在例外,比如在RL(强化学习)中,我们不直接计算梯度,而是去估计梯度。 举个例子,我们教一个机器人学习骑车,它经常摔来摔去。 这时候我们可以让目标函数是自行车不摔倒的累计时长。 不幸的是,这种目标函数无法计算梯度。 我们的机器人需要自己探索,去找到适合它自己的骑车的方法。
虽然 RL 的代价函数在多数情况下不可微分,神经网络依然可以适用梯度相关的方法去学习。 这是监督学习和强化学习的主要区别之一。 在强化学习里,代价函数 C C C 不可微分。 实际上它是完全未知的。 像一个黑箱子一样,你给它一些输入,它返回一些输出,你并不知道正确答案是什么,只有 y ˉ 和 C \bar{y}和C yˉ和C,能做的只是改变 y ˉ \bar{y} yˉ看C会怎么改变。 这也导致 RL 非常低效,尤其当参数向量维度很高的时候(换言之,算法需要在巨大的空间里探索,寻找解决方案)。
在RL里,有一种非常常用的方法叫做 Actor Critic(演员-评论家)。 其中,评论家模块有一个自己的代价函数C,这个模块是已知并且可训练的。 这个模块是可微分的,人们训练这个模块去近似真正的代价函数或者奖励(reward)函数。 这样以来,人们就可以用可微分的函数去近似代价函数,从而进行反向传播。
2.1.2 在传统神经网络中随机梯度下降和反向传播算法的优势
随机梯度下降的优势
在实际操作中,我们利用随机梯度下降算法来计算目标函数在参数上的梯度。 相比于在所有样本上计算目标函数的梯度,再进行平均,随机梯度下降算法每步只选取一个样本,计算损失 L L L,进而获取损失函数在训练参数上的梯度值。 之后,随机梯度下降算法在这个梯度的反方向上移动一步。
w ← w − η ∂ L ( x [ p ] , y [ p ] , w ) ∂ w w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w} w←w−η∂w∂L(x[p],y[p],w)
在这个公式中,我们用 w w w 减去步长乘以上述的(基于每个样本 x [ p ] , y [ p ] x[p],y[p] x[p],y[p] 的损失计算出的)梯度值,而得到新的 w w w。
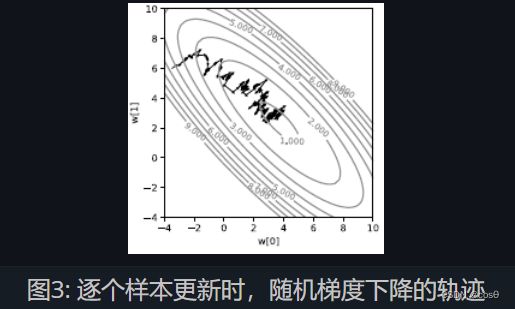
因为基于每个样本进行计算,我们得到的轨迹存在非常大的干扰,如图3所示。 我们计算出的损失并不是直指山下,而是看起来非常随机。 每个样本都会把我们的损失拽向各不一样的方向。 不过平均来看,这些小的移动把我们带去了山谷。 虽然看起来有点低效,这种方法其实比起在整批样本上做梯度下降要快得多,尤其是当样本之间有很多重复信息的时候。
在实际中,我们并不用单个样本做随机梯度下降,相反,我们每次更新用一小批的样本(minibatch)。 我们计算一小批样本的平均梯度,然后移动一小步。 我们这么做的唯一原因是因为这样可以更有效地优化算法,让它们更适应当前的硬件(比如GPU,多核CPU)。 批量运算是一种简单的并行化运算方法。
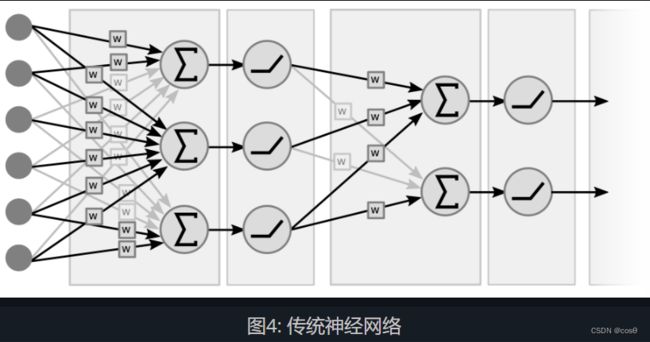
传统神经网络
传统的神经网络由互相穿插的线性运算和逐点非线性运算构成。 其中,线性运算就是矩阵-向量乘法,我们将(输入)向量与权值矩阵相乘。 之后,我们将相乘之后的加权和(向量)进行非线性运算(比如 ReLU ( ⋅ ) , tanh ( ⋅ ) , … ) \texttt{ReLU}(\cdot), \tanh(\cdot), …) ReLU(⋅),tanh(⋅),…)
图4所示是一个两层的神经网络,图中可以看到两对线性-非线性层。 也有人称这个网络为三层网络,因为他们包括了输入变量。 注意,当没有中间的非线性层时,这个网络有可能会转化成一个单层网络,因为两个线性函数的乘积依然是一个线性函数。
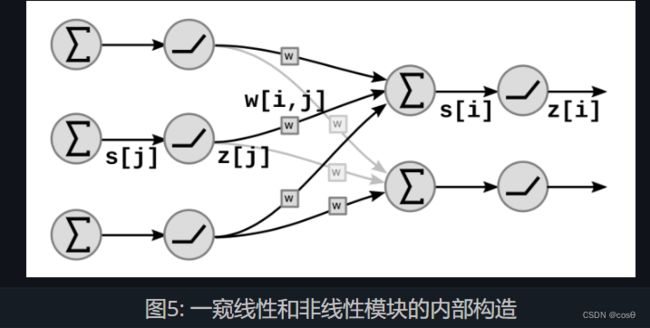
在图中, s [ i ] s[i] s[i]代表了单位 i {i} i 的加权和:
s [ i ] = ∑ j ∈ U P ( i ) w [ i , j ] ⋅ z [ j ] s[i]=\sum_{j \in UP(i)}w[i,j]\cdot z[j] s[i]=j∈UP(i)∑w[i,j]⋅z[j]
其中 U P ( i ) UP(i) UP(i)表示 i i i之前一层的单位, z [ j ] z[j] z[j] 是之前一层的第 j j j个输出。
从而我们计算 z [ i ] z[i] z[i] 用:
z [ i ] = f ( s [ i ] ) z[i]=f(s[i]) z[i]=f(s[i])
其中 f f f 是非线性函数。
具体这里涉及到的微积分的知识可以参照3Blue1Brown的深度学习课程
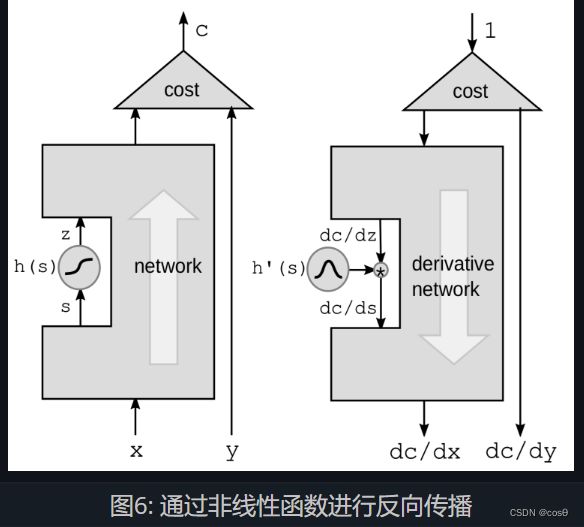
通过非线性函数进行反向传播
我们要介绍的第一种方法,是通过非线性函数进行的反向传播。 我们从神经网络里单拿出非线性函数 h h h(即上面的 f f f) ,忽略黑盒子里的其他部分。
这里我们利用链式法则来计算梯度:
g ( h ( s ) ) ′ = g ′ ( h ( s ) ) ⋅ h ′ ( s ) g(h(s))' = g'(h(s))\cdot h'(s) g(h(s))′=g′(h(s))⋅h′(s)
其中, h ’ ( s ) h’(s) h’(s) 是 z z z对 s s s的导数,即 d z d s \frac{\mathrm{d}z}{\mathrm{d}s} dsdz 。 为了更清楚地表示这个导数,我们改写上面的公式为:
d C d s = d C d z ⋅ d z d s = d C d z ⋅ h ′ ( s ) \frac{\mathrm{d}C}{\mathrm{d}s} = \frac{\mathrm{d}C}{\mathrm{d}z}\cdot \frac{\mathrm{d}z}{\mathrm{d}s} = \frac{\mathrm{d}C}{\mathrm{d}z}\cdot h'(s) dsdC=dzdC⋅dsdz=dzdC⋅h′(s)
这样以来,我们只要可以用串联的一系列函数来表示一个神经网络,我们就可以逐层乘以每个 h {h} h函数的导数,从而进行反向传播。
我们也可以用扰动法的角度去想这个问题。 对 s s s添加 d s \mathrm{d}s ds 的扰动,会相应地在 z z z上添加如下扰动:
d z = d s ⋅ h ′ ( s ) \mathrm{d}z = \mathrm{d}s \cdot h'(s) dz=ds⋅h′(s)
从而,这也会在 C C C上添加如下扰动:
d C = d z ⋅ d C d z = d s ⋅ h ’ ( s ) ⋅ d C d z \mathrm{d}C = \mathrm{d}z\cdot\frac{\mathrm{d}C}{\mathrm{d}z} = \mathrm{d}s\cdot h’(s)\cdot\frac{\mathrm{d}C}{\mathrm{d}z} dC=dz⋅dzdC=ds⋅h’(s)⋅dzdC
这样以来,我们得到了和之前一样的公式。
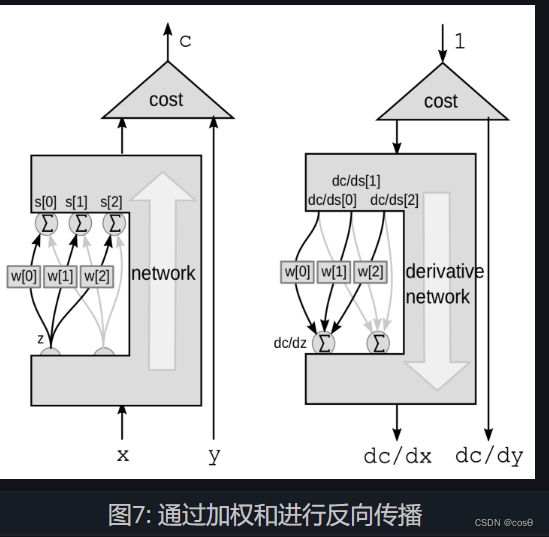
通过加权和进行反向传播
对于线性模块,我们通过加权和进行万象传播。 这次,我们关注变量 z z z和那一系列变量 s s s之间的连接,默认其他的部分是黑盒子。
这次,扰动是一个加权和。 z z z会对多个变量造成影响。 对 z z z施加扰动 d z \mathrm{d}z dz,对相应对 s [ 0 ] s[0] s[0], s [ 1 ] s[1] s[1]和 s [ 2 ] s[2] s[2]施加如下扰动:
d s [ 0 ] = w [ 0 ] ⋅ d z \mathrm{d}s[0]=w[0]\cdot \mathrm{d}z ds[0]=w[0]⋅dz
d s [ 1 ] = w [ 1 ] ⋅ d z \mathrm{d}s[1]=w[1]\cdot \mathrm{d}z ds[1]=w[1]⋅dz
d s [ 2 ] = w [ 2 ] ⋅ d z \mathrm{d}s[2]=w[2]\cdot\mathrm{d}z ds[2]=w[2]⋅dz
相似地,这会对 C C C 施加如下扰动:
d C = d s [ 0 ] ⋅ d C d s [ 0 ] + d s [ 1 ] ⋅ d C d s [ 1 ] + d s [ 2 ] ⋅ d C d s [ 2 ] \mathrm{d}C = \mathrm{d}s[0]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[0]}+\mathrm{d}s[1]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[1]}+\mathrm{d}s[2]\cdot\frac{\mathrm{d}C}{\mathrm{d}s[2]} dC=ds[0]⋅ds[0]dC+ds[1]⋅ds[1]dC+ds[2]⋅ds[2]dC
因此 C C C会受到三个变量的影响而改变,将三个变量对C变化的贡献加起来。
d C d z = d C d s [ 0 ] ⋅ w [ 0 ] + d C d s [ 1 ] ⋅ w [ 1 ] + d C d s [ 2 ] ⋅ w [ 2 ] \frac{\mathrm{d}C}{\mathrm{d}z} = \frac{\mathrm{d}C}{\mathrm{d}s[0]}\cdot w[0]+\frac{\mathrm{d}C}{\mathrm{d}s[1]}\cdot w[1]+\frac{\mathrm{d}C}{\mathrm{d}s[2]}\cdot w[2] dzdC=ds[0]dC⋅w[0]+ds[1]dC⋅w[1]+ds[2]dC⋅w[2]
2.1.3 一个神经网络和反向传播的PyTorch实现
一个传统神经网络的方块图表示
- 线性模块表示为
s k + 1 = w k z k s s_{k+1}=w_kz_ks sk+1=wkzks
- 非线性模块表示为
z k = h ( s k ) z z_k=h(s_k)z zk=h(sk)z

w k w_k wk 是矩阵; z k z_k zk是向量; h h h 是一个函数,它对输入的每一个元素调用 h {h} h函数。 如图所示是一个三层神经网络,这个神经网络由一系列的线性-非线性函数对组成。 大多数现代神经网络并不像图中所示的例子一样具有这么清晰的结构,它们一般来说要更加复杂。
PyTorch实现
import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()
class mynet(nn.Module):
def __init__(self, d0, d1, d2, d3):
super().__init__()
self.m0 = nn.Linear(d0, d1)
self.m1 = nn.Linear(d1, d2)
self.m2 = nn.Linear(d2, d3)
def forward(self,x):
z0 = x.view(-1) # flatten input tensor
s1 = self.m0(z0)
z1 = torch.relu(s1)
s2 = self.m1(z1)
z2 = torch.relu(s2)
s3 = self.m2(z2)
return s3
model = mynet(d0, 60, 40, 10)
out = model(image)
- 运用PyTorch,我们可以用面向对象的方法来实现神经网络。 首先,我们定义一个神经网络的类,在构造方法中,可以用PyTorch里用定义的 nn.Linear 类去初始化线性层。 我们需要分别为每一个线性层定义不同的对象,因为每个对象会包含自己的参数向量。 nn.Linear类还提供了偏置向量,它会被加到输出里。 接下来,我们定义一个前向传播函数,我们用 torch.relu \text{torch.relu} torch.relut 作为非线性激活函数。 我们不用定义多个 ReLU 函数,因为它不包含参数,所以可以被共用。
- 我们不用自己自己算梯度,因为PyTorch会根据我们提供的前向传播函数,自己计算用于反向传播的梯度。
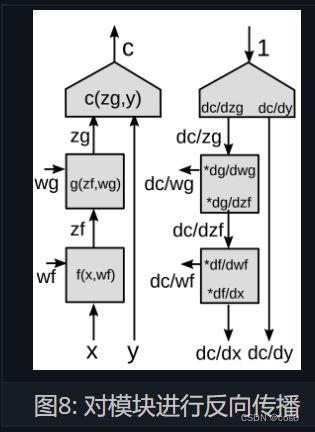
对于一个模块进行反向传播
下面我们展示一个反向传播的例子。
一个功能模块可能具有多个输入和多个输出,也有可能输入是向量输出也是向量。
- 在向量函数中使用链式法则
z g : [ d g × 1 ] , c o l u n m v e c t o r z_g : [d_g\times 1],colunm\ vector zg:[dg×1],colunm vector
z f : [ d f × 1 ] z_f:[d_f\times 1] zf:[df×1]
∂ c ∂ z f = ∂ c ∂ z g ∂ z g ∂ z f \frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}} ∂zf∂c=∂zg∂c∂zf∂zg
[ 1 × d f ] = [ 1 × d g ] × [ d g × d f ] [1\times d_f]= [1\times d_g]\times[d_g\times d_f] [1×df]=[1×dg]×[dg×df]
这是利用链式法则计算 ∂ c ∂ z f \frac{\partial c}{\partial{z_f}} ∂zf∂c的基本公式。 值得注意的是,一个标量对于一个向量的梯度,是一个和这个向量同样形状的一个向量。 我们统一用行向量而非列向量去表示这些向量(梯度)。
对于上面的式子,我们可以进行转置,这样输出的偏导数仍然为列向量,但要注意乘法顺序发生变化了
∂ c ∂ z f T = ∂ z g ∂ z f T ∂ c ∂ z g T \frac{\partial c}{\partial{z_f}}^T=\frac{\partial {z_g}}{\partial{z_f}}^T\frac{\partial c}{\partial{z_g}}^T ∂zf∂cT=∂zf∂zgT∂zg∂cT
[ d f × 1 ] = [ d f × d g ] × [ d g × 1 ] [d_f\times 1]= [d_f\times d_g]\times[d_g\times 1] [df×1]=[df×dg]×[dg×1]
-
雅可比矩阵(一阶偏导数矩阵)
( ∂ z g ∂ z f ) i j = ( ∂ z g ) i ( ∂ z f ) j \left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j} (∂zf∂zg)ij=(∂zf)j(∂zg)i
利用 ∂ z g ∂ z f \frac{\partial {z_g}}{\partial {z_f}} ∂zf∂zg (雅可比矩阵的元),通过已知代价函数对于 z g z_g zg的梯度,我们可以计算代价函数对于 z f z_f zf的梯度。 每一个元 i j ij ij 等于输出向量的第 i i i个元素对于输入向量第 j j j个元素的偏导数。
当网络中有一系列串联的模块,我们可以在每一层用乘雅可比矩阵的方法一路向下,从而得到每个变量的梯度值。
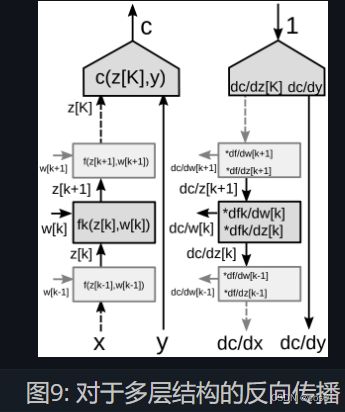
对于多层结构的反向传播
设想一个由多个模块堆叠的神经网络,如图9所示。
在反向传播算法中,我们需要两套梯度:一套是对于状态(网络中的每一个模块)的梯度,另一套是对于权值(某一个模块中所有的参数)的梯度值。 因此,对于每个模块,我们需要两个雅可比矩阵。 这里我们再次利用链式法则完成反向传播。
- 对向量函数使用链式法则
∂ c ∂ z k = ∂ c ∂ z k + 1 ∂ z k + 1 ∂ z k = ∂ c ∂ z k + 1 ∂ f k ( z k , w k ) ∂ z k \frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}} ∂zk∂c=∂zk+1∂c∂zk∂zk+1=∂zk+1∂c∂zk∂fk(zk,wk)
∂ c ∂ w k = ∂ c ∂ z k + 1 ∂ z k + 1 ∂ w k = ∂ c ∂ z k + 1 ∂ f k ( z k , w k ) ∂ w k \frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}} ∂wk∂c=∂zk+1∂c∂wk∂zk+1=∂zk+1∂c∂wk∂fk(zk,wk)
- 模块中的两个雅可比矩阵
1. 对于 z [ k ] z[k] z[k]
2. 对于 w [ k ] w[k] w[k]
2.2 为神经网络的模组计算梯度,与反向传播的实用技巧
2.2.1 一个反向传播的具体例子还有介绍基础的神经网络模组
范例
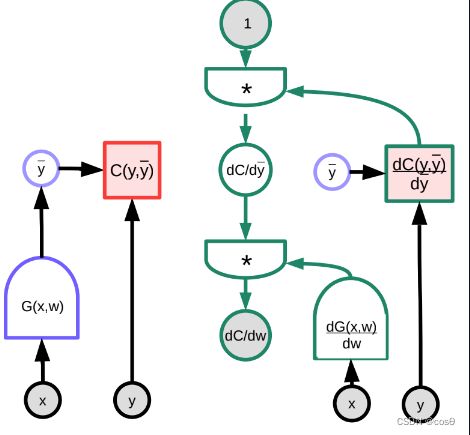
接下来我们会考虑一个反向传播的例子,并使用图像来辅助。任意的函数 G ( w ) G(w) G(w)输入到损失函数 C C C中,这可以用一个图来表示。经由雅可比矩阵的乘法操作,我们能将这个图转换成一个反向计算梯度的图。(注意 Pytorch 和 Tensorflow 已经自动地为使用者完成这件事了,也就是说,向前的图自动的被「倒反」来创造导函数的图形以反向传播梯度。)
在这个范例中,右方的绿色图代表梯度的图。跟着图从最上方的节点开始的是:
∂ C ( y , y ˉ ) ∂ w = 1 ⋅ ∂ C ( y , y ˉ ) ∂ y ˉ ⋅ ∂ G ( x , w ) ∂ w \frac{\partial C(y,\bar{y})}{\partial w}=1 \cdot \frac{\partial C(y,\bar{y})}{\partial\bar{y}}\cdot\frac{\partial G(x,w)}{\partial w} ∂w∂C(y,yˉ)=1⋅∂yˉ∂C(y,yˉ)⋅∂w∂G(x,w)
从维度来说, ∂ C ( y , y ˉ ) ∂ w \frac{\partial C(y,\bar{y})}{\partial w} ∂w∂C(y,yˉ)是一个行向量,大小为 1 × N 1\times N 1×N,其中N是w中成员的数量; ∂ C ( y , y ˉ ) ∂ y ˉ \frac{\partial C(y,\bar{y})}{\partial \bar{y}} ∂yˉ∂C(y,yˉ)是个大小 1 × M 1\times M 1×M 的行向量,其中 M M M是输出的维度; ∂ y ˉ ∂ w = ∂ G ( x , w ) ∂ w \frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w} ∂w∂yˉ=∂w∂G(x,w)是个大小 M × N M\times N M×N 的矩阵,其中 M M M是 G G G输出的数量,而 N N N是 w w w 的维度。
注意当图的结构不固定而是依赖于数据时,情况可能更为复杂。比如,我们可以根据输入向量的长度来选择神经网络的模组。虽然这是可行的,当迭代数量过度增加,处理这个变化的难度会增加。
基本的神经网络模组
除了习惯的线性和 ReLU 模组,还有其他预先建立的模组。他们十分有用因为他们为了各自的功能被特别的优化过(而非只是用其他初阶模组拼凑而成)。
-
线性: Y = W ⋅ X Y=W\cdot X Y=W⋅X
d C d X = W ⊤ ⋅ d C d Y d C d W = d C d Y ⋅ X ⊤ \begin{aligned} \frac{dC}{dX} &= W^\top \cdot \frac{dC}{dY} \\ \frac{dC}{dW} &= \frac{dC}{dY} \cdot X^\top \end{aligned} dXdCdWdC=W⊤⋅dYdC=dYdC⋅X⊤ -
ReLU: y = ( x ) + y=(x)^+ y=(x)+
d C d X = { 0 x < 0 d C d Y otherwise \frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{otherwise} \end{cases} dXdC={0dYdCx<0otherwise
- 重复: Y 1 = X , Y 2 = X Y_1=X, Y_2=X Y1=X,Y2=X
- 如同一个「分接线」,两个输出都与输入相同(e.g 两个人听同一首歌)
- 反向传播时,梯度相加
- 可以类似的分配成 n n n个分支
d C d X = d C d Y 1 + d C d Y 2 \frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2} dXdC=dY1dC+dY2dC
- 相加: Y = X 1 + X 2 Y=X_1+X_2 Y=X1+X2
当两个变数相加,其中一个若被改变,输出也会以相同幅度改变,即
d C d X 1 = d C d Y ⋅ 1 and d C d X 2 = d C d Y ⋅ 1 \frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1 dX1dC=dYdC⋅1anddX2dC=dYdC⋅1
-
最大值: Y = max ( X 1 , X 2 ) Y=\max(X_1,X_2) Y=max(X1,X2)
因为这个函数也可以写作:
Y = max ( X 1 , X 2 ) = { X 1 X 1 > X 2 X 2 else ⇒ d Y d X 1 = { 1 X 1 > X 2 0 else Y=\max(X_1,X_2)=\begin{cases} X_1 & X_1 > X_2 \\ X_2 & \text{else} \end{cases} \Rightarrow \frac{dY}{dX_1}=\begin{cases} 1 & X_1 > X_2 \\ 0 & \text{else} \end{cases} Y=max(X1,X2)={X1X2X1>X2else⇒dX1dY={10X1>X2else
因此,根据链式法则
d C d X 1 = { d C d Y ⋅ 1 X 1 > X 2 0 else \frac{dC}{dX_1}=\begin{cases} \frac{dC}{dY}\cdot1 & X_1 > X_2 \\ 0 & \text{else} \end{cases} dX1dC={dYdC⋅10X1>X2else
2.2.2 LogSoftMax vs SoftMax
Pytorch中Softmax、Log_Softmax、NLLLoss以及CrossEntropyLoss的关系与区别详解
softmax的log似然代价函数(公式求导)
交叉熵softmax求导简单解释
SoftMax,另一个 Pytorch 模组,是一种方便的方式,可以将一组数字转换为0到1之间的数值,并使它们和为 1。这些数字可以理解为概率分布。因此,它经常用于分类问题。下方等式中的 y i y_i yi是一个记录着每一个类别概率的向量
y i = exp ( x i ) ∑ j exp ( x j ) y_i = \frac{\exp(x_i)}{\sum_j \exp(x_j)} yi=∑jexp(xj)exp(xi)
然而,使用 softmax 使网络容易面临梯度消失。梯度消失是一个问题,因为它会使得随后的权重无法被神经网络改动,进而停止神经网络进一步训练。Logistic sigmoid 函数,就是单一数值的 Softmax 函数,展现出当 s s s很大时, h ( s ) h(s) h(s)是 1 1 1,而当 s s s很小时, h ( s ) h(s) h(s)是 0。因为 sigmoid 函数在 h ( s ) = 0 h(s) = 0 h(s)=0 和 h ( s ) = 1 h(s) = 1 h(s)=1处是平坦的,其梯度为0,造成消失的梯度。
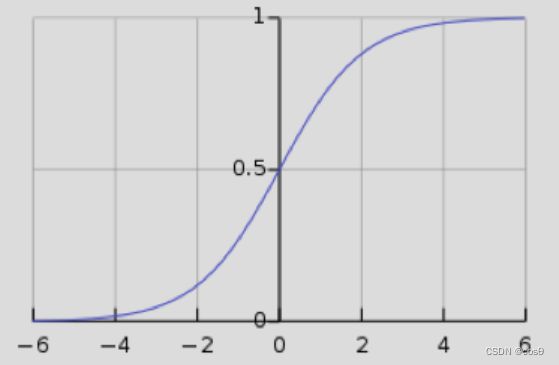
h ( s ) = 1 1 + e x p ( − s ) h(s)= \frac{1}{1+exp(−s)} h(s)=1+exp(−s)1
数学家想到可以用 logsoftmax 来解决 softmax 造成的梯度消失问题。LogSoftMax 是 Pytorch 当中的另一个基本模组。正如下方等式所示,LogSoftMax 组合了 softmax 和对数。
log ( y i ) = log ( exp ( x i ) Σ j exp ( x j ) ) = x i − log ( Σ j exp ( x j ) \log(y_i )= \log\left(\frac{\exp(x_i)}{\Sigma_j \exp(x_j)}\right) = x_i - \log(\Sigma_j \exp(x_j) log(yi)=log(Σjexp(xj)exp(xi))=xi−log(Σjexp(xj)
下方的等式提供同一个等式的另一种观点。下图显示函数中 log ( 1 + exp ( s ) ) \log(1 + \exp(s)) log(1+exp(s))的部份。当s非常小,其值为0,至于s很大时,值是s。如此一来,它不会造成饱和,就避免了梯度消失。
log ( exp ( s ) exp ( s ) + 1 ) = s − log ( 1 + exp ( s ) ) \log\left(\frac{\exp(s)}{\exp(s) + 1}\right)= s - \log(1 + \exp(s)) log(exp(s)+1exp(s))=s−log(1+exp(s))
2.2.3 反向传播的实用技巧
用 ReLU 作为非线性函数
对于有很多层的网络,ReLU 的效果最好,甚至使其他函数如 sigmoid、hyperbolic tangent tanh ( ⋅ ) \tanh(\cdot) tanh(⋅)相形之下过时了。ReLU 很有效的原因可能是因为它具有的一个尖点使它具有缩放的等变性。
用交叉熵作为分类问题的损失函数
在讲座里前面提到的 Log softmax是交叉熵损失的特例。Pytorch 里,请保证传给交叉熵损失函数时要使用 Log softmax 为输入(而非一般 softmax)。
训练时使用小批量(minibatch)的随机梯度下降
如同之前所讨论的,小批量使你能更有效率的训练,因为数据中有重复;你不需要每一步对每个观察进行预测、计算损失以估计梯度。
训练时打乱样本顺序
顺序会造成影响。如果模型在一回的训练中只有来自同一类别的样本,它会去直接预测该类别而非学习为何要预测该类别。例如,如果你试着分类 MNIST 数据集的数字而没有打乱数据,那最后一层的偏置易开始总会预测零,接着改成总是预测一、二,依此类推。理想上,每个批量中都应该要有来自每个类别的样本。
不过是否要在每回(epoch)的训练都改变次序仍然存在争论。
将输入归一化使其具有零平均值与单位方差
训练之前,先归一化每个输入特征,让均值为0、标准差为1是很有用的。使用 RGB 图像数据时,经常会单独取每个通道的均值和标准差,以通道为单位进行归一化。举例而言,取数据集中所有蓝色通道的数值的均值 m b m_b mb 和标准差 σ b \sigma_b σb ,接着归一化每个图像的蓝色通道数值如下:
b [ i , j ] ′ = b [ i , j ] − m b max ( σ b , ϵ ) b_{[i,j]}^{'} = \frac{b_{[i,j]} - m_b}{\max(\sigma_b, \epsilon)} b[i,j]′=max(σb,ϵ)b[i,j]−mb
其中 ϵ \epsilon ϵ 是个任意小的数字,用于避免除以零。对绿色通道和红色通道进行同样操作。这个必要的操作使我们能从不同光线下的图像取得有用的信号;例如日光中的相片有很多红色,但水下的图片则几乎没有。
按照进度递减学习率
随着训练持续,学习率应该下降。实际上,大多进阶的模型是用 Adam/Momentum 这些能自我调整学习率的算法训练的,而非学习率固定的单纯 SGD。
使用 L1 和(或)L2 正则化进行权重衰减
机器学习中正则化项L1和L2的直观理解
你可以在损失函数中附上对巨大权重的损失。例如,使用 L2 正则化,我们定义损失为 L L L 并且如下更新权重 w w w,且 R ( w ) = ∥ w ∥ 2 R(w) = \Vert w \Vert^2 R(w)=∥w∥2:
L ( S , w ) = C ( S , w ) + α ∥ w ∥ 2 ∂ R ∂ w i = 2 w i w i = w i − η ∂ C ∂ w i = w i − η ( ∂ C ∂ w i + 2 α w i ) L(S, w) = C(S, w) + \alpha \Vert w \Vert^2\\ \frac{\partial R}{\partial w_i} = 2w_i \\ w_i = w_i - \eta\frac{\partial C}{\partial w_i} = w_i - \eta(\frac{\partial C}{\partial w_i} + 2 \alpha w_i) L(S,w)=C(S,w)+α∥w∥2∂wi∂R=2wiwi=wi−η∂wi∂C=wi−η(∂wi∂C+2αwi)
为了理解为何这称作权重衰减,我们可以将上方的方程式重写来展现我们在更新时把 w i w_i wi 乘以一个小于一的常数。
w i = ( 1 − 2 η α ) w i − η ∂ C ∂ w i w_i = (1 - 2 \eta \alpha) w_i - \eta\frac{\partial C}{\partial w_i} wi=(1−2ηα)wi−η∂wi∂C
L1 正则化(Lasso)是类似的,只不过我们使用 ∑ i ∣ w i ∣ \sum_i \vert w_i\vert ∑i∣wi∣而不是 ∥ w ∥ 2 \Vert w \Vert^2 ∥w∥2 。
本质上,正则化尝试告诉系统要以最短的权重向量来最小化损失函数。L1 正则化会将无用的权重缩减至 0。
权重初始化
权重要被随机的初始化,但它们不能太大或太小,因为输出得要有与输入差不多的方差。Pytorch 有诸多内建的初始化技巧。其中一个适合深层模型的是 Kaiming 初始化:权重的方差与输入数量的平方根成反比。
使用 dropout
Dropout 是另一种正则化。它可以当做神经网络的另一层:它接受输入,随机将 n / 2 n/2 n/2 的输入设为零,并且回传这个结果为输出。这迫使系统从所有输入单元获得信息而不是过度依赖少数的输入单元,从而能将资讯分配于一层中的所有单元。这个方法最初是由Hinton et al (2012)提出。
更多技巧参见 LeCun et al 1998.
最后,注意反向传播不只适用于层层堆叠的模型;它可用于任何有向无环图(DAG)只要模组间具有偏序关系,
2.3 人工神经网络(ANNs)
2.3.1 进行分类的监督学习
-
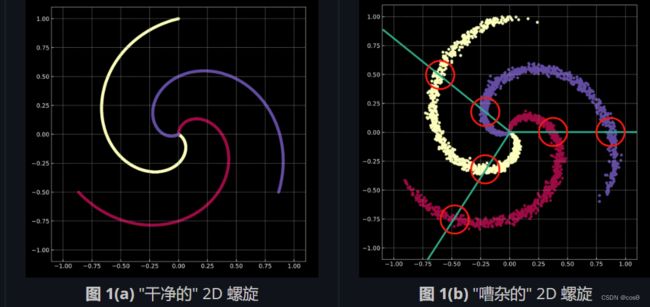
看看底下的 图 1(a) 。图中的点分布在这个螺旋的旋臂上,并且是在 R 2 \R^2 R2中。每个颜色代表一个类别标记。总共有 K = 3 K = 3 K=3 个不同的类别。数学上由 方程式 1(a) 表示。
-
图 1(b) 展现了一个类似的螺旋,加上高斯噪声。它的数学表示是 方程式 1(b) 。
在两个例子中,这些点都不是线性可分的。
X k ( t ) = t ( sin [ 2 π K ( 2 t + k − 1 ) ] cos [ 2 π K ( 2 t + k − 1 ) ] ) 0 ≤ t ≤ 1 , k = 1 , . . . , K X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K Xk(t)=t(sin[K2π(2t+k−1)]cos[K2π(2t+k−1)])0≤t≤1,k=1,...,K
X k ( t ) = t ( sin [ 2 π K ( 2 t + k − 1 + N ( 0 , σ 2 ) ) ] cos [ 2 π K ( 2 t + k − 1 + N ( 0 , σ 2 ) ) ] ) 0 ≤ t ≤ 1 , X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, Xk(t)=t(sin[K2π(2t+k−1+N(0,σ2))]cos[K2π(2t+k−1+N(0,σ2))])0≤t≤1,
进行分类是什么意思呢?请想想看逻辑回归 (LR) 的情况。如果用逻辑回归来分类这个数据,它会创造一系列的线性平面(决策边界)以尝试分离数据到各自的类别。这种解法存在问题,那就是每个区域中,都有属于不同类别的点。因为螺旋的悬臂会跨越决策边界,这不是一个好的解法。
我们该如何解决这个问题?我们可以变换输入空间,使得数据变的线性可分。在训练一个神经网络的过程,它所习得的决策边界会试着符合训练数据的分布。
注意:一个神经总是用由下而上的方式来表示。第一层在最底下,最后一层在顶端。这是因为概念上,输入数据对神经网络处理的任务而言是低阶的特征。当资料向上遍历网络时,每一层会提取更高阶的特征。
2.3.2 训练数据
上周,我们看到刚初始化的神经网络会任意的变换它的输入。这个变换(起初)对完成眼下的任务没有功效。我们来探索如何用数据来使这个变换具有与手边的任务有关的含义。下列是用来训练的输入数据。
- X \boldsymbol X X 代表输入数据,一个 m × n m \times n m×n的矩阵( m m m是数据点的数量, n n n 是每个输入点的维度)。在图1(a) 和 1(b) 的例子 n = 2 \mathbf n = 2 n=2.
- c \boldsymbol c c 和 Y \boldsymbol Y Y都是代表这 m m m数据点中每一个点属于的类别。在前述的例子中,共有3个不同的类别。
- c i ∈ 1 , 2 , … , K c_i \in {1, 2, …, K} ci∈1,2,…,K 和 c ∈ R m × 1 \boldsymbol c \in \R^{m \times 1} c∈Rm×1 。然而 Y \mathbf Y Y并不 ∈ R m × 1 \in \R^{m \times 1} ∈Rm×1 ,亦即我们不用 \mathbf cc 作为训练数据。如果我们使用这些不同的数字类别标记 c i ∈ 1 , 2 , … , K c_i \in {1, 2, …, K} ci∈1,2,…,K,网络可能会推断出类别的顺序,而这是不能代表数据分布的。
- 为了绕过这个问题,我们使用one-hot 编码。我们为每个数据点建立一个 K K K维的向量 y ( i ) \boldsymbol y^{(i)} y(i),其第 i个元素设为 1( i ∈ 1 , 2 , … , K i \in {1, 2, …, K} i∈1,2,…,K是数据点们的类别标记,如图 3)。
- 故 Y ∈ R m × K \boldsymbol Y \in \R^{m \times K} Y∈Rm×K 。这个矩阵也可以想成是有着完全集中在 K点其中一点的几率质量。
2.3.3全连接层(fully connected (FC) layer)
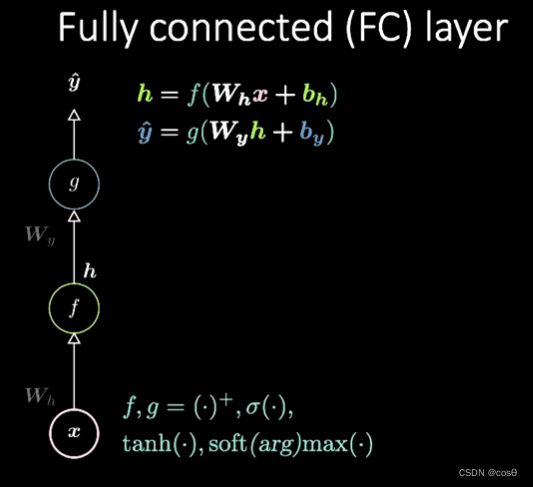
考虑图 4所描绘的网络。输入数据, x \boldsymbol x x,受到由 W h \boldsymbol W_h Wh 定义的仿射变换,再经过一个非线性变换。非线性变换的结果表示为 h \boldsymbol h h,代表一个隐藏的输出,也就是一个从网路外部看不见的输出。接下来又有另一个仿射变换( W y \boldsymbol W_y Wy)以及非线性变换,于是产出最终的输出 y ^ \boldsymbol{\hat{y}} y^ 。这个网络可以用下方的方程2来表示,其中 f f f和 g g g都是非线性函数。
h = f ( W h x + b h ) y ^ = g ( W y h + b y ) \begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned} h=f(Whx+bh)y^=g(Wyh+by)
之前看到的这样基础的神经网络只是一连串先仿射变换再非线性运算(挤压)的搭配。常用的非线性函数包含 ReLU、sigmoid、hyperbolic tangent 和 softmax。
上面展示的网络是一个 3 层的网络
1 - 输入神经元
2 - 隐藏神经元
3 - 输出神经元
因此,一个 3层的神经网络有 2个仿射变换。这可以类推至 n 层的网络。
现在让我们看看更复杂的例子。
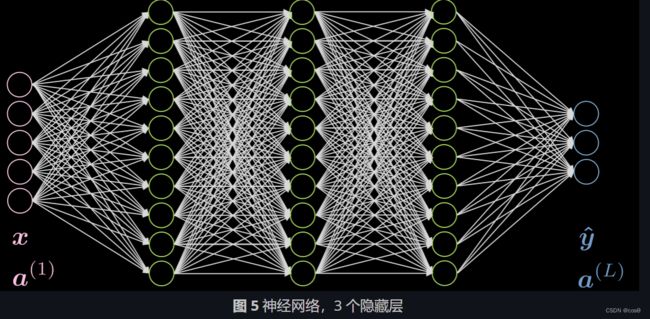
这个网络有 3 个隐藏层,每一层都是全连接的。图 5 描绘了这个网络。
来考虑第二层的神经元 jj。它的激活值是: a j ( 2 ) = f ( w ( j ) x + b j ) = f ( ( ∑ i = 1 n w i ( j ) x i ) + b j ) ) a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big) aj(2)=f(w(j)x+bj)=f((∑i=1nwi(j)xi)+bj)) 其中 w ( j ) \boldsymbol w^{(j)} w(j) 是 W ( 1 ) \boldsymbol W^{(1)} W(1) 的第 j 行。
注意在此例中输入层的激活函数只是恒等函数。隐藏层的激活函数可以是 ReLU、hyperbolic tangent、sigmoid、soft (arg)max 等等。
最后一层的激活函数通常取决于使用情况,这篇 Piazza post 提供了一个解释。
2.3.4 神经网络(推断 (inference))
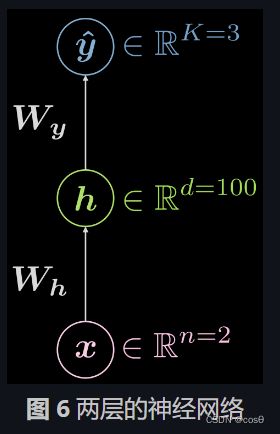
让我们再次考虑两层的神经网络(输入层,隐藏层,输出层),见图 6
这个函数是什么样子的呢?
y ^ = y ^ ( x ) , y ^ : R n → R K , x ↦ y ^ \boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}} y^=y^(x),y^:Rn→RK,x↦y^
不过,将视隐藏层视觉化会很有帮助,这样,这个映射关系就被扩展为:
y ^ : R n → R d → R K , d ≫ n , K \boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K y^:Rn→Rd→RK,d≫n,K
这个情况的范例构造长什么样子?在我们的例子里,输入的维度是2(n=2),有一个 1000 维(d = 1000)的隐藏层,以及三个类别(C = 3)。就实际而言,有很多好的理由不在一个隐藏层中放这么多神经元,所以我们可以把这一个隐藏层换成三个各具有 10 个神经元的隐藏层( 1000 → 10 × 10 × 10 1000 \rightarrow 10 \times 10 \times 10 1000→10×10×10)。

2.3.5 神经网络(训练 I)
那么典型的训练是如何?我们最好用损失(losses)的标准术语来阐述这个过程。
首先,来重新介绍 soft (arg)max 并明确的说:它是一个最后一层经常使用的激活函数,用于搭配 negative log-likelihood loss 处理多类别预测。如同 LeCun 教授在讲座中所说,这是因为它提供比 sigmoid 与均方误差更好的梯度。而且,使用 soft (arg)max 时,你的最后一层已经被归一化(最后一层中所有神经元输出的和为 1),以一种对于梯度方法来说较显性归一化(除以范数)更好的方法。
soft (arg)max 会给你最后一层的 logit,如下:
soft(arg)max ( l ) [ c ] = exp ( l [ c ] ) ∑ k = 1 K exp ( l [ k ] ) ∈ ( 0 , 1 ) \text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1) soft(arg)max(l)[c]=∑k=1Kexp(l[k])exp(l[c])∈(0,1)
必须注意这不是一个闭区间因为指数函数自然会产生正值。
给定预测值的集合 Y ^ \hat{Y} Y^ ,损失函数值是:
L ( Y ^ , c ) = 1 m ∑ i = 1 m ℓ ( y ^ ( i ) , c i ) , ℓ ( y ^ , c ) = − log ( y ^ [ c ] ) \mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}^{(i)}}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c]) L(Y^,c)=m1i=1∑mℓ(y^(i),ci),ℓ(y^,c)=−log(y^[c])
L \mathcal{L} L表示的是对所有输入样本,每个样本求cost值的和的平均值; ℓ \ell ℓ表示一个样本的cost; y ^ \hat{y} y^是一个表示神经网络输出的向量(在这个例子中包含了三个元素); y ^ [ c ] \hat{y}[c] y^[c]表示的是这个项链里的第c个元素;这里 c 表示整数的标记而非 one-hot 编码的表示方法。
那么我们来做两个例子,其一的数据被正确分类的数据,另一个不是。
比方
x , c = 1 ⇒ y = ( 1 0 0 ) \boldsymbol{x}, \quad c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}} x,c=1⇒y=(100)
每一笔数据的损失是多少呢?
如果是接近完美的预测 ( ∼ \sim ∼ 的意思是 大约):
y ^ ( x ) = ( ∼ 1 ∼ 0 ∼ 0 ) ⇒ ℓ ( ( ∼ 1 ∼ 0 ∼ 0 ) , 1 ) → 0 + \hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+} y^(x)=(∼1∼0∼0)⇒ℓ((∼1∼0∼0),1)→0+
因为此时 y ^ [ c ] = y ^ [ 1 ] = 1 \hat{y}[c] = \hat{y}[1] = 1 y^[c]=y^[1]=1,而-log(1) = 0.
如果是几乎完全错误:
y ^ ( x ) = ( ∼ 0 ∼ 1 ∼ 0 ) ⇒ ℓ ( ( ∼ 0 ∼ 1 ∼ 0 ) , 1 ) → + ∞ \hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty y^(x)=(∼0∼1∼0)⇒ℓ((∼0∼1∼0),1)→+∞
因为此时 y ^ [ c ] = y ^ [ 1 ] = 0 \hat{y}[c] = \hat{y}[1] = 0 y^[c]=y^[1]=0,而-log(0) = + ∞ \infty ∞.
注意在上面的例子中, ∼ 0 → 0 + ∼ 0 → 0 + a n d ∼ 1 → 1 − \sim 0 \rightarrow 0^{+}∼0→0 +and \sim 1 \rightarrow 1^{-} ∼0→0+∼0→0+and∼1→1− 。为何如此,请稍为思考一下。
补充:有关softmax的内容可以看这个资料
注意:当你使用CrossEntropyLoss,就同时具备了LogSoftMax和 negative loglikelihood NLLLoss,所以不要用了
2.3.6 神经网络 (训练 II)
做训练时,我们集结所有可以训练的参数--权重矩阵和偏置--于一个集合 Θ = { W h , b h , W y , b y } \mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace Θ={Wh,bh,Wy,by}}。所以我们可以把目标函数,也就是损失,写成:
J ( Θ ) = L ( Y ^ ( Θ ) , c ) ∈ R + J \left( \Theta \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \Theta \right), \boldsymbol c \right) \in \mathbb{R}^{+} J(Θ)=L(Y^(Θ),c)∈R+
这使得损失取决于网络的输出 Y ^ ( Θ ) \boldsymbol {\hat{Y}} \left( \Theta \right) Y^(Θ),所以我们可以将其转换为一个优化问题。
在图 7当中你可以看到它如何进行, J ( v ) J(\mathcal{v}) J(v) 是我们想最小化的函数。
我们挑选一个随机初始化的点 ϑ 0 \vartheta_0 ϑ0 – 它对应的损失是 J ( ϑ 0 ) J(\vartheta_0) J(ϑ0)。我们可以计算在该点的导数 J ’ ( ϑ 0 ) = d J ( ϑ ) d ϑ ( ϑ 0 ) J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0) J’(ϑ0)=dϑdJ(ϑ)(ϑ0)。这个例子里,导数的斜率是正的。我们要向下降最陡的方向走一步。在此是 - d J ( ϑ ) d ϑ ( ϑ 0 ) \frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0) dϑdJ(ϑ)(ϑ0)
这个迭代重复的过程被称作梯度下降。梯度的方法是训练神经网络的主要工具。
为了计算必要的梯度,我们要使用反向传播。
∂ J ( Θ ) ∂ W y = ∂ J ( Θ ) ∂ y ^ ∂ y ^ ∂ W y ∂ J ( Θ ) ∂ W h = ∂ J ( Θ ) ∂ y ^ ∂ y ^ ∂ h ∂ h ∂ W h \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}} ∂Wy∂J(Θ)=∂y^∂J(Θ)∂Wy∂y^∂Wh∂J(Θ)=∂y^∂J(Θ)∂h∂y^∂Wh∂h