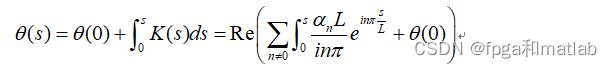基于PSO优化VIC算法的WORM蠕虫检测matlab仿真
目录
一、理论基础
二、案例背景
1.问题描述
2.思路流程
三、部分MATLAB程序
四、仿真结论分析
五、算法相关应用
六、参考文献
一、理论基础
根据参考文献:
初始条件
计算曲率
角度的计算公式
那么对于坐标点,其满足如下的计算公式,
二、案例背景
1.问题描述
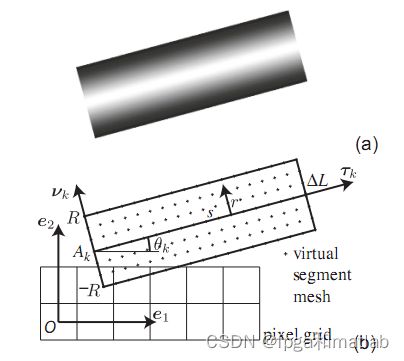
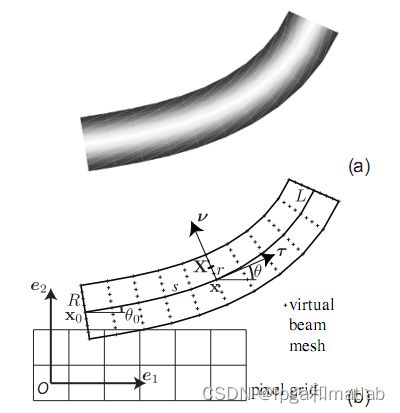
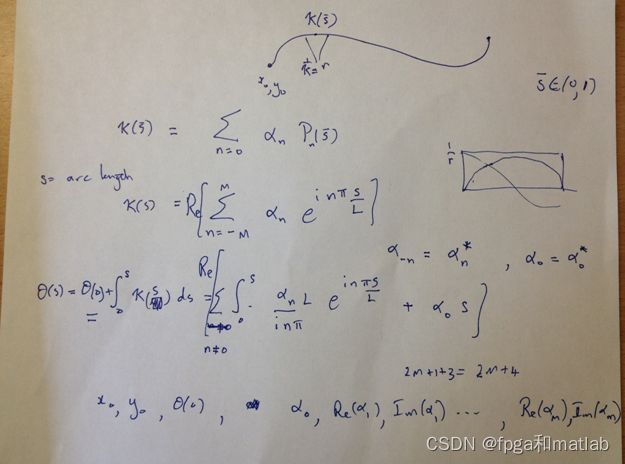
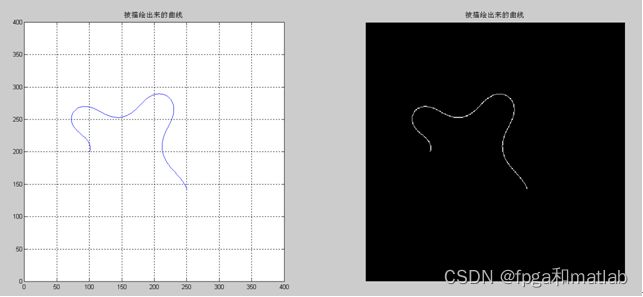
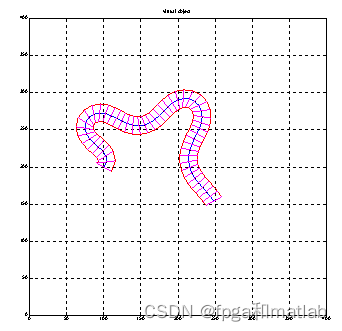
给定一组初始值,构造出虚拟图。初始值就是如下图图一 x0, y0, θ(0)那行,给出曲线的初始点和初始角度,构造出曲线。曲线中的current point x的坐标可以由θ(s)求出,θ(s)可以由初始值求出。 如下图一所示 K(s)是一条曲线的曲率,用傅里叶级数表达然后求出角θ(s),这样,这条曲线就被描绘出来了,然后用这条曲线构造一个virtual object,如图二所示。 这个object 是曲线以半径r外扩得到的长条形曲面,如图所示。
2.思路流程
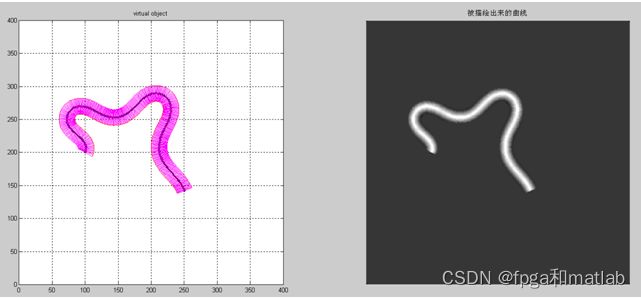
本课题我们主要通过VIC算法检测得到曲线的中线,然后根据这个中线进行扩展,得到光滑曲线体,本课题的这个研究过程和实际的蠕虫建模方法非常的接近,这是由于光滑曲线体和蠕虫的建模,他们都是通过中线检测进行的。此外,本课题还对传统的VIC算法进行了改进,通过使用PSO粒子群优化算法,从而大大提供的光滑曲线的建模精度。
通过PSO粒子群优化算法,对原有的VIC算法进行参数进行优化,从而得到更高精度的虚拟曲线的建模。通过仿真对比可知,采用优化算法之后的虚拟曲线,其精度比原算法的精度提高了10倍以上。
三、部分MATLAB程序
VIC算法部分:
function I2 = func_Virtual_Image(X,Y,X_img,Y_img,L,Ls,r,theta);
%然后用这条曲线构造一个virtual object,如图二所示。 这个object 是曲线以半径r外扩得到的长条形曲面,如图所示。
%进行扩展
I2 = 50*ones(L,L);
for kk = 1:r
X1 = zeros(L/Ls,1);
Y1 = zeros(L/Ls,1);
X2 = zeros(L/Ls,1);
Y2 = zeros(L/Ls,1);
for i = 1:L/Ls
if mod(sum(theta(1:i)),180) < 0
X1(i) = X(i) + kk*cos(pi*theta(i)/180);
Y1(i) = Y(i) - kk*sin(pi*theta(i)/180);
X2(i) = X(i) - kk*cos(pi*theta(i)/180);
Y2(i) = Y(i) + kk*sin(pi*theta(i)/180);
else
X1(i) = X(i) + kk*cos(pi/2 - pi*theta(i)/180);
Y1(i) = Y(i) - kk*sin(pi/2 - pi*theta(i)/180);
X2(i) = X(i) - kk*cos(pi/2 - pi*theta(i)/180);
Y2(i) = Y(i) + kk*sin(pi/2 - pi*theta(i)/180);
end
end
%将X和Y曲线变化为实际图像信息
for i = 1:L/Ls
Xp1(i) = floor(X1(i));
Yp1(i) = floor(Y1(i));
Xp2(i) = floor(X2(i));
Yp2(i) = floor(Y2(i));
end
X_img1 = L-Yp1;
Y_img1 = Xp1;
X_img2 = L-Yp2;
Y_img2 = Xp2;
for i = 1:L/Ls
I2(X_img(i),Y_img(i)) = 255;
if r==1
I2(X_img1(i),Y_img1(i)) = 255 - kk*120;
I2(X_img2(i),Y_img2(i)) = 255 - kk*120;
end
if r==2
I2(X_img1(i),Y_img1(i)) = 255 - kk*90;
I2(X_img2(i),Y_img2(i)) = 255 - kk*90;
end
if r==3
I2(X_img1(i),Y_img1(i)) = 255 - kk*80;
I2(X_img2(i),Y_img2(i)) = 255 - kk*80;
end
if r==4
I2(X_img1(i),Y_img1(i)) = 255 - kk*60;
I2(X_img2(i),Y_img2(i)) = 255 - kk*60;
end
if r==5
I2(X_img1(i),Y_img1(i)) = 255 - kk*50;
I2(X_img2(i),Y_img2(i)) = 255 - kk*50;
end
if r==6
I2(X_img1(i),Y_img1(i)) = 255 - kk*40;
I2(X_img2(i),Y_img2(i)) = 255 - kk*40;
end
if r==7
I2(X_img1(i),Y_img1(i)) = 255 - kk*35;
I2(X_img2(i),Y_img2(i)) = 255 - kk*35;
end
if r==8
I2(X_img1(i),Y_img1(i)) = 255 - kk*30;
I2(X_img2(i),Y_img2(i)) = 255 - kk*30;
end
if r==9
I2(X_img1(i),Y_img1(i)) = 255 - kk*25;
I2(X_img2(i),Y_img2(i)) = 255 - kk*25;
end
if r==10
I2(X_img1(i),Y_img1(i)) = 255 - kk*25;
I2(X_img2(i),Y_img2(i)) = 255 - kk*25;
end
if r==11
I2(X_img1(i),Y_img1(i)) = 255 - kk*23;
I2(X_img2(i),Y_img2(i)) = 255 - kk*23;
end
if r==12
I2(X_img1(i),Y_img1(i)) = 255 - kk*21;
I2(X_img2(i),Y_img2(i)) = 255 - kk*21;
end
if r==13
I2(X_img1(i),Y_img1(i)) = 255 - kk*19;
I2(X_img2(i),Y_img2(i)) = 255 - kk*19;
end
if r==14
I2(X_img1(i),Y_img1(i)) = 255 - kk*18;
I2(X_img2(i),Y_img2(i)) = 255 - kk*18;
end
if r==15
I2(X_img1(i),Y_img1(i)) = 255 - kk*17;
I2(X_img2(i),Y_img2(i)) = 255 - kk*17;
end
if r==16
I2(X_img1(i),Y_img1(i)) = 255 - kk*16;
I2(X_img2(i),Y_img2(i)) = 255 - kk*16;
end
end
end
I2 = medfilt2(I2,[5,5]);
PSO优化:
while iterfpbest(i)
fpbest(i) = J;
Xpbest(:,i) = X(:,i);
end
end
[fitnessmax,index]=max(fpbest);
if fitnessmax>fgbest
fgbest=fitnessmax;
Xgbest=X(:,index);
end
for i=1:N
r1 = rand;
r2 = rand;
fai1 = C1*r1;
fai2 = C2*r2;
V(:,i) = w(iter) * V(:,i) +fai1 *( Xpbest(:,i) - X(:,i) ) +
fai2 * ( Xgbest(:,1) - X(:,i) );
index = find(abs(V(:,i))>Vmax);
if(any(index))
V(index,i) = V(index,i)./abs(V(index,i)).*Vmax;
end
X(:,i) = X(:,i)+V(:,i);
end
fgbest_fig(iter) = fgbest;
Xgbest_fig(:,iter) = Xgbest;
alpha(1) = Xgbest_fig(1,iter);
alpha(2) = Xgbest_fig(2,iter);
alpha(3) = Xgbest_fig(3,iter);
V_scores = func_cal_score(alpha,L,m,Theta,Ls,Xt,Yt,r,I2);
V_score2(iter) = V_scores;
end
VIC算法的主程序调用:
............................
%然后用这条曲线构造一个virtual object,如图二所示。 这个object 是曲线以半径r外扩得到的长条形曲面,如图所示。
%进行扩展
X1 = zeros(L/Ls,1);
Y1 = zeros(L/Ls,1);
X2 = zeros(L/Ls,1);
Y2 = zeros(L/Ls,1);
for i = 1:L/Ls
if mod(sum(theta(1:i)),180) < 0
X1(i) = X(i) + r*cos(pi*theta(i)/180);
Y1(i) = Y(i) - r*sin(pi*theta(i)/180);
X2(i) = X(i) - r*cos(pi*theta(i)/180);
Y2(i) = Y(i) + r*sin(pi*theta(i)/180);
else
X1(i) = X(i) + r*cos(pi/2 - pi*theta(i)/180);
Y1(i) = Y(i) - r*sin(pi/2 - pi*theta(i)/180);
X2(i) = X(i) - r*cos(pi/2 - pi*theta(i)/180);
Y2(i) = Y(i) + r*sin(pi/2 - pi*theta(i)/180);
end
end
if Ls == 1
figure;
subplot(121)
plot(X,Y,'b');hold on;
plot(X,Y,'k.');hold on;
plot(X1,Y1,'r');hold on;
plot(X2,Y2,'r');hold on;
for i = 1:length(X)
line([X2(i),X1(i)],[Y2(i),Y1(i)],'Color',[1 0 1]);hold on;
end
title('virtual object');
grid on
axis square
axis([0,L,0,L]);
else
figure;
plot(X,Y,'b');hold on;
plot(X,Y,'k.');hold on;
plot(X1,Y1,'r');hold on;
plot(X2,Y2,'r');hold on;
for i = 1:length(X)
line([X2(i),X1(i)],[Y2(i),Y1(i)],'Color',[1 0 1]);hold on;
end
title('virtual object');
grid on
axis square
axis([0,L,0,L]);
end
%产生虚拟图像
%将X和Y曲线变化为实际图像信息
I2 = func_Virtual_Image(X,Y,X_img,Y_img,L,Ls,r,theta);
if Ls == 1
subplot(122)
imshow(I2,[])
title('被描绘出来的曲线');
axis square
end
四、仿真结论分析
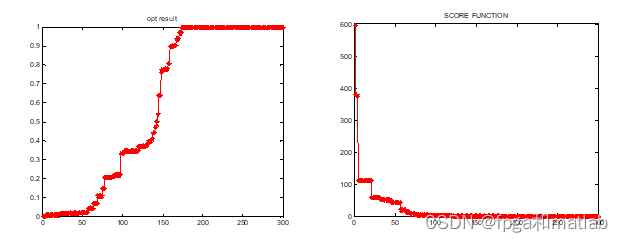
从上面的仿真结果可知,通过粒子群优化之后,系统的Score值不断逼近0,这说明通过粒子群优化之后,得到的光滑曲线值的精度达到了最大值。从左图可知,当系统的优化达到优化预期时,系统的最佳适应度值达到最佳值,接近1。
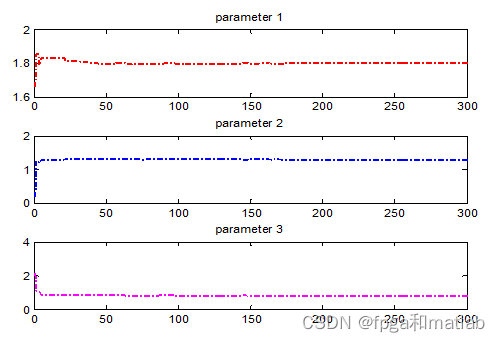
从上图的仿真结果可知,当优化之后,系统的仿真参数达到收敛预期。最后输出的参数值,就可以使系统的曲线建模达到最高精度。
五、算法相关应用
通过所研究的VIC算法,可以有效检测输出医学上的蠕虫检测,从而提高医学诊断等目标 。
六、参考文献
[1] Semin B , Auradou H , Francois M . Curvilinear shapes by Virtual Image Correlation[J]. Europhysics News, 2011, 42(6):p.17-18.A10-10&12