机器学习算法学习笔记：集成学习

一、理论篇

1、概述

生活中，当做重要决定时，通常都会考虑吸取多个人的意见而不只是一个人的意见。集成学习也是如此。集成学习就是组合多个单一的、独立的学习器，最后可以得到一个比单一学习器泛化性能更好的学习器。

正所谓“三个臭皮匠赛过诸葛亮”的道理，在机器学习数据挖掘的工程项目中，使用单一决策的弱分类器显然不是一个明智的选择，因为各种分类器在设计的时候都有自己的优势和缺点，也就是说每个分类器都有自己工作偏向，那集成学习就是平衡各个分类器的优缺点，使得我们的分类任务完成的更加优秀。

根据个体学习器的生成方式，目前的集成学习方法大致可以分成两类：第一类就是个体学习器之间不存在很强的依赖关系，学习器可以并行生成，代表方法：Bagging 和Random Forest。第二类是单个学习器之间有着很强的依赖关系，需要以串行的序列化的方式生成，代表方法：Adaboost、GBDT、XGBoost等等。

2、Bagging和Boosting

2.1 Bagging

Bagging（Bootstrap Aggregating）又称为套袋法/装袋法：每次从样本集合中有放回地抽取n个值，一共抽取k轮，形成k个训练集合，训练集合之间彼此独立。对于分类问题，k个训练器可以训练出k个模型，从而产生k个结果，对于回归问题，取均值作为预测结果。

Bagging个体学习器之间不存在强依赖关系！

【基本思想流程图】

【算法流程】

• 对训练集随机采样；
• 分别基于不同的样本集合训练n个弱分类器；
• 对每个弱分类器输出预测结果；
• 根据结合策略得出最终分类预测。

2.2 Boosting

每次拿整个样本进行训练，根据结果调整每次训练的参数，使模型效果逐渐变好。

梯度提升的Boosting方法则是使用代价函数对上一轮训练的损失函数f的偏导数来拟合残差。

样本权值和模型权值：Boosting会减小在上一轮正确样本的权重，增大错误样本的权重（因为正确样本残差小，错误样本残差大）。组合模型的时候会将错误率高的模型赋予低的权重，将错误率低的模型赋予高的权重，有助于增加组合后模型准确率。

2.3 Bagging和Boosting的区别

• 训练数据集：

Bagging是每次从样本集中有放回地抽取n个样本，抽取k次，形成k个样本集合，样本集合之间相互独立；

Boosting则是训练集合保持不变，每次变化的是训练集中样例的权重。

• 样例权重：

Bagging使用的是均匀采样，每个样例权重相等；

Boosting根据上一轮结果调整权重，错误率越大权重越大。

• 预测函数：

Bagging所有的预测函数权重相同；

Boosting预测函数权重不同，预测误差小的权重越大。

• 并行计算：

Bagging各个预测函数可以并行生成；

Boosting只能顺序生成，因为后一个预测要用到上一个结果。

3、Random Forest

RF = DT(Decision Tree)+Bagging+随机属性选择。

【算法流程】

• 1.样本的随机：从样本集中用Bagging的方式，随机选择n个样本。
• 2.特征的随机：从所有属性d中随机选择k个属性(k
• 3.重复以上两个步骤m次，建立m棵CART决策树。
• 4.这m棵CART决策树形成随机森林，通过投票表决结果，决定数据属于哪一类。

4、Adaboost

Adaboost最初的想法是由Robert E. Schapire在1990年提出的，这个想法叫做自适应增强方法。与Bagging相比，Boosting思想可以降低偏差。

提升（Boosting）个体学习器之间存在强依赖关系！

AdaBoost是英文“Adaptive Boosting”（自适应增强）的缩写，它的自适应在于：前一个基本分类器被错误分类的样本的权值会增大（意味着下次被抽中的概率增大），而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。

【基本思想】将学习器的重点放在“容易”出错的样本上，可以提升学习器的性能。

【算法流程】

• 初始化训练数据的权值分布$D_1$。假设有N个训练样本数据，则每一个训练样本最开始时，都被赋予相同的权值：$w_1$=1/N。
• 训练弱分类器$h_i$。具体训练过程中是：如果某个训练样本点，被弱分类器$h_i$准确地分类，那么在构造下一个训练集中，它对应的权值要减小；相反，如果某个训练样本点被错误分类，那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
• 将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换而言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

【例子】给定下表所示的训练数据。假设弱分类器有xv产生，其阈值$v$使该分类器在训练数据集上分类误差率最低。使用Adaboost算法学习一个强分类器。

5、GBDT

6、XGBoost

7、结合策略

• 对于回归问题，采用算术平均法或者加权平均法；
• 对于分类问题，采用相对多数投票法（少数服从多数）或者加权投票法。
• 学习法

当训练数据很多时，更加强大的结合策略就是学习法，也就是通过另一个学习器来进行组合。典型代表是Stacking。把个体学习器称之为初级学习器，用于结合的学习器称为次级学习器或者元学习器。

Stacking先从初始训练集训练出初级学习器，然后生成一个新的数据集来训练次级学习器。新的数据集是以初级学习器的输出作为样例，初始样本的标记被当做样例标记。

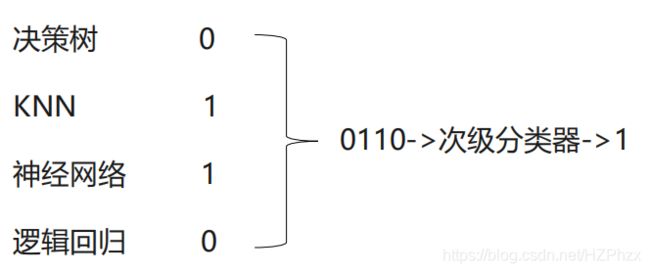
Stacking算法可以理解为一个两层的集成，第一层含有一个分类器，把预测的结果(元特征)提供给第二层， 而第二层的分类器通常是逻辑回归，他把一层分类器的结果当做特征做拟合输出预测结果。

使用多个不同的分类器对训练集进预测，把预测得到的结果作为一个次级分类器的输入。次级分类器的输出是整个模型的预测结果。