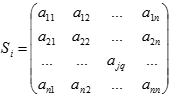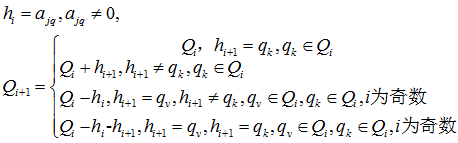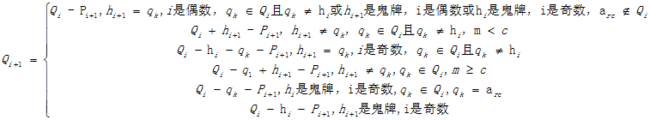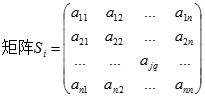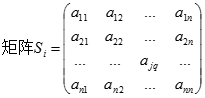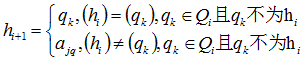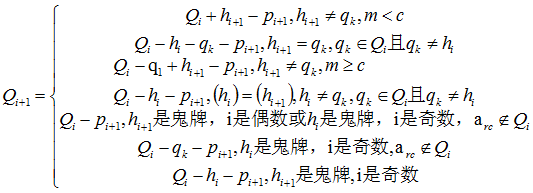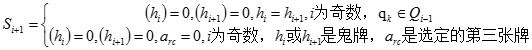【数学建模论文】北邮hzg2014模拟D题

 本文系原创，欢迎转载，转载请注明出处http://www.cnblogs.com/windcarp/

Purple Place游戏的优化翻牌策略

陈星曼 魏淙铭 田桃

摘要：寻找规范的翻牌策略，即希望找到一种方法，使得在游戏中，能够用尽量少的翻牌次数，将全部图片配对并从牌桌上完全去除（称为最优策略）。在数学上可以视为随机优化模型，目标在于计算算法的最优化。针对这个问题，本文采用常见的数据结构如队列和矩阵等对游戏进行建模分析，运用贪心法等得出策略，并对策略进行优化。

模型一中我们基于当翻开的纸牌在记忆队列中存在相同图案的纸牌时，立即消去的策略。采用该策略可以记忆更多的纸牌，同时使翻牌次数较少。充分考虑在游戏过程中是否有连续（连续两张翻过的牌图案相同）消去的情况，进行详细的分析与证明，从而证得策略一具有最优记忆队列空间数目。

模型二中我们基于当第一次翻开的纸牌在记忆队列中存在相同图案的纸牌时，立即消去的策略。该策略力求使每一张纸牌的翻牌次数为1，从而使翻牌总次数最少。充分考虑在游戏过程中是否有连续（连续两张翻过的牌图案相同）消去的情况，进行详细的分析与证明，从而得出模型二适用于规模较小的翻牌游戏的结论。

最后通过编程对算法进行实现，通过大量实验验证算法的有效性，并针对不同情况进行分析和建议。

关键字：翻牌，算法，优化，贪心法

 

1 题目重述

Vista提供了一款游戏Purple Place。游戏提供一副经过随机排序处理、按照某种规则（比方4*4、6*6矩形状）排布、背面朝外的一些图卡。图卡具有一致的背面图案，通常按照图卡数为偶数分成若干组，每组的正面图案相同。通过点击鼠标的方式随意揭开某张图卡使其正面朝上，但同时正面朝上的图卡的累积张数不能超过两张：如果被揭开的两张图片图案相同，则这两张图片将被从牌桌上"成功"去除；否则，则自动恢复背面朝上，而这正是考验记忆力好坏的关键。基于玩家超常的记忆力、辅助合适的翻牌策略，实现用尽可能少的翻牌次数将全部图片配对并从牌桌上完全去除。

显然一个好的翻牌策略是重要的，这不光可以直接节约翻牌次数，同时规则的翻牌方式事实上也总是帮助玩家更容易记起那些曾经翻过而又被重新合上的图片的图案，进而取得好成绩。

利用数学建模的方法，采用适当的数据形式，对这一游戏的实现进行建模分析，寻找好的算法，得到更为规范的翻牌策略。

 

2 问题分析

这是一个寻找规范的翻牌策略的问题，通过这个规范的翻牌策略节约翻牌次数，同时帮助记忆曾经翻开过又被重新合上的牌的图案。我们知道，在一次游戏中，翻牌次数的多少要受到纸牌的排列，翻牌的策略选择，游戏玩家的记忆状态等各种因素的影响。

问题中明显带有随机因素影响且不可忽略，且求解的目标在于找到优化算法，因此可以视为随机优化模型。在解决一个随机问题时，我们得出的策略可能不会直接得到最优的解，但是当实验次数较多时，我们仍然可以给出一个算法使平均的翻牌次数（期望）较小以达到我们的目标，实现计算算法的最优化。我们可以采用常见的数据结构如队列和矩阵等对游戏进行建模分析，并对策略进行优化。

 

3 模型假设

根据游戏的规则以及解决问题的需要假设如下。

（1）假设游戏玩家的记忆状态稳定，即在整个游戏过程中，能一直保持最多记住相同数量的纸牌的图案。

（2）假设游戏玩家对纸牌的每一种图案的记忆能力是相同的。

（3）假设当已记忆的纸牌数量超过游戏玩家的最大记忆能力时，游戏玩家会将最先记忆的纸牌图案遗忘，同时保证记忆纸牌数目维持在最大记忆能力。

（4）假设游戏界面上只有一张纸牌正面朝上时，下次将点击其他纸牌。

（5）假设点击到鬼牌时，游戏玩家下一次将点击尚未记住的纸牌。

（6）假设点击到鬼牌时，消去的第三张纸牌选取与已翻开的非鬼牌具有相同图案且是行数最小的所有纸牌中列数最小的纸牌。

（7）比较采用不同策略时完成游戏的翻牌次数，假设纸牌的排列顺序、游戏玩家的记忆状态等其他因素均相同。

 

4 符号说明

表1 符号说明

n	游戏的规格
stimes	总点击次数
d	游戏中纸牌的图案总的种类数
	游戏中，第j行第q列的纸牌的图案。 当时，表示图案已消去 当时，表示图案未消去
c	游戏玩家最多能记住的牌的数目
	游戏玩家能记住的牌
	第次翻牌后，游戏玩家的记忆队列
	这张纸牌上的图案
	表示在第i次翻牌和第i+1次翻牌过程中遗忘的纸牌集合
	中干扰间隔次数
	第次翻的牌
	第次翻的纸牌上的图案

 

 

 

5 模型建立

为寻找这个规范的翻牌策略，我们用矩阵来表示游戏中的图片排列，用队列来表示游戏玩家的记忆空间。每一次翻牌之后，矩阵和队列会随之变化。由于游戏中，图片的各种图案的排列是随机的，所以可针对各种可能的情况，建立数学模型如下。

游戏的对象为纸牌，对纸牌所处的状态描述为：

其中，表示游戏中，第j行第q列的纸牌的图案 ，当时，表示图案已消去；当时，表示图案未消去(。

游戏考察玩家的记忆能力，将玩家的记忆描述为一个队列：

其中表示游戏玩家能记住的牌。

对规则的描述如下：

 

6 模型分析

翻牌策略大致可分为两类：①发现相同图案的牌后，立即消去；②先记忆部分牌的图案再将相同图案的牌消去。

采用第一类策略的平均翻牌次数小于采用第二类策略的平均总翻牌次数。因为对于奇数次点翻开的牌，若已知与牌图案相同的牌。采用策略一，下次翻开对于翻牌次数为1，而采用第二类策略次数大于1，因此本文对第二类策略不予详细分析。

策略一中，对于偶数次翻开的牌，若中存在与图案相同的牌，则再次翻开和，将其消去，对于下一张图案相同的牌添加到记忆队列，其翻牌次数大于等于2，为减少其翻牌次数，我们提出了策略二，对于第次翻牌中存在使得时，若是奇数，则,将与消去；若是偶数，则将添加到记忆序列。

 

 

 

 

7 算法模型一与分析

 

此模型是基于当翻开的纸牌在记忆队列中存在相同图案的纸牌时，立即消去的策略。采用该策略可以记忆更多的纸牌，同时使翻牌次数较少。

⑴当翻牌时，没有连续（即连续两张翻过的牌图案相同）消去的情况出现时，

①第次翻牌后，游戏中纸牌所处状态的矩阵的建立：

其中，表示游戏中，第j行、第q列的纸牌的图案 ，当时，表示图案已消去；当时，表示图案未消去；

②游戏玩家的记忆能力的队列的建立：

其中表示，游戏玩家能记住的牌

③游戏玩家的遗忘队列的建立:

④第i+1次翻牌后，有

其中表示第i+1次翻的牌

⑤第i+1次翻牌后，有

⑥第i+1次翻牌之后，游戏玩家的记忆空间状态变为

其中，是选定的第三张纸牌。

⑦此时，矩阵的状态变为

⑵当翻牌时，出现连续（即连续两张翻过的牌图案相同）消去的情况出现时，

①第次翻牌后，游戏中纸牌所处状态的矩阵的建立：

其中，表示游戏中，第j行第q列的纸牌的图案 ，当时，表示图案已消去；当时，表示图案未消去；

②游戏玩家的记忆能力的队列的建立：

其中表示，游戏玩家能记住的牌

③游戏玩家的遗忘的队列的建立:

④第i+1次翻牌后，有

其中表示第i+1次翻的牌

⑤第i+1次翻牌后，有

⑥第i+1次翻牌之后，游戏玩家的记忆空间状态变为

⑦此时，矩阵的状态变为

当记忆队列充满后，再次翻牌会将原队列中纸牌删除，翻过的牌被遗忘后，其翻牌策略次数增加。翻牌策略可通过提高记忆队列空间数目，减少总翻牌次数，策略一具有最优记忆队列空间数目。

 

对于策略的分析与证明：

按一定的顺序翻牌，记忆更多的图案可转化为使记忆队列未填充的空间尽可能大。

对于任意的翻牌顺序,,...,,不考虑连续消去的情况，即对每一张牌均从上次翻牌前已记忆的牌中消去，找到相同图案的纸牌。

贪心选择证明：假设存在一个最优解策略A，不包含对第张采用模型一，策略B为对第张牌采用模型一，其他牌同策略A。

当第张牌能立即消去时，采用模型一后的记忆队列未填充空间小于未采用模型一的记忆队列未填充空间。

当第张牌未能立即消去时，采用模型一后的记忆队列未填充空间等于未采用模型一的记忆队列未填充空间。

所以策略B的记忆队列未填充空间小于等于策略A的记忆队列未填充空间。

所以策略B是一个最优解，即存在最优策略包含模型一。

最优子结构证明：以模型一得到最优解C，第i张牌翻开后，假设余下的牌以模型一得到的解D不是部分最优解，部分最优解为E，则C-D+E的记忆队列未填充空间小于C的记忆队列未填充空间，则C不是最优解，矛盾。

即证得模型一。

 

8 算法模型二与分析

此模型是基于当第一次翻开的纸牌在记忆队列中存在相同图案的纸牌时，立即消去的策略。该策略力求使每一张纸牌的翻牌次数为1，从而使翻牌总次数最少。

⑴当翻牌时，没有连续（即连续两张翻过的牌图案相同）消去的情况出现时，

①第i次翻牌后，游戏中纸牌所处状态的矩阵的建立：

其中，表示游戏中，第j行第q列的纸牌的图案 ，当时，表示图案已消去；当时，表示图案未消去；

②游戏玩家的记忆能力的队列的建立：

其中表示，游戏玩家能记住的牌。

③游戏玩家的遗忘队列的建立:

④第i+1次翻牌后，有

其中表示第i+1次翻的牌

⑤第i+1次翻牌后，有

⑥第i+1次翻牌之后，游戏玩家的记忆空间状态变为

⑦此时，矩阵的状态变为

⑵当翻牌时，出现连续（即连续两张翻过的牌图案相同）消去的情况出现时，

①第i次翻牌后，游戏中纸牌所处状态的矩阵的建立：

其中，表示游戏中，第j行第q列的纸牌的图案 ，当时，表示图案已消去；当时，表示图案未消去；

②游戏玩家的记忆能力的队列的建立：

其中表示，游戏玩家能记住的牌

③游戏玩家的遗忘队列的建立:

④第i+1次翻牌后，有

其中表示第i+1次翻的牌

⑤第i+1次翻牌后，有

    ⑥第i+1次翻牌之后，游戏玩家的记忆空间状态变为

⑦此时，矩阵的状态变为

对于第次翻牌中存在使得时，若是奇数，则,将与消去；若是偶数，则将添加到记忆序列。

若是偶数，当下一张牌,,翻开时，若k为奇数，将同消去，此时翻牌次数为1,，而采取模型一时翻牌次数为2。若下一张牌，,翻开之前，已从队列Q删除，则采用模型二的翻牌次数大于2.

对于策略的分析与证明：

经计算可得，当c取7时，对于的翻牌游戏，在记忆队列未充满前出现奇数次，的可消的概率约为.由短时记忆规律可知，人的短时记忆可持续20秒，因此对于规模较小的翻牌游戏，已翻过的牌被遗忘的概率小，此时采用模型二，未立即消去相同牌产生的遗忘负担较小，而总翻牌次数小。当c取7时，对于的翻牌游戏，在记忆队列未充满前，出现奇数次可消的概率为0.49.此时，模型二因未立即消去相同牌产生的遗忘负担增大，不宜采用模型二。

综上，模型二适用于规模较小的翻牌游戏。

 

 

9 模型检验

我们的目标是求得对于翻牌问题的优化算法，其具体表现则为平均点击次数最少。因为在模型中存在很多随机的因素，比如每一次游戏中牌的排列次序所导致的连续两次点击恰好相同、"鬼牌"的出现等。为了验证上述两个模型的可行性与有效性，我们编写程序模拟这两种算法对牌的操作，通过大量实验进行验证。编写源程序代码见附录。

根据模型分析，以及查阅资料[1][2][3]所知，短时记忆信息保持时间比较短，在无复述的情况下只能保持5-20秒，最长不超过1分钟，而且人的大脑记忆容量有限，一般为。这里我们对两种算法分别取记忆时间为5,6…20s，假设我们1秒钟点击一轮（2张牌），则记忆牌的张数取5,6,…60张。同时取记忆容量取为5,7,9,11来进行测试，测试的游戏难度为（5*5）和（6*6），每一种情况测试次数为10 000次。

测试结果（点击次数）采用Mathematica绘制图像如下所示，表格如附录所示。以5*5中游戏两种算法的表现为例，6*6中游戏两种算法的表现图见附录。

算法1：

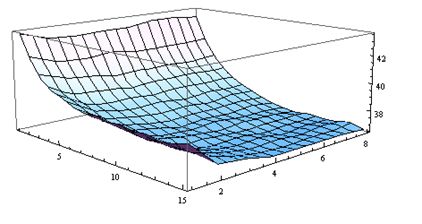
图1 算法1在5*5游戏中实验结果

算法2：

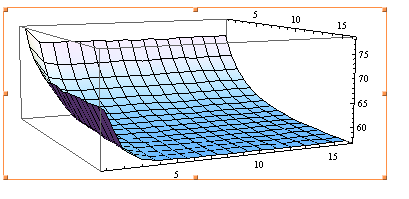
图2 算法2在5*5游戏中实验结果

 

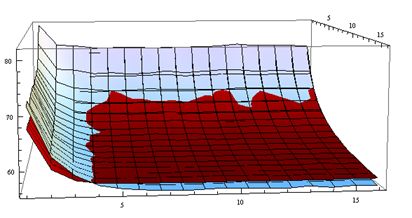
图3 算法1、2在5*5游戏中比较实验结果

图4 算法1、2在6*6游戏中比较实验结果

数据分析：对于5*5的矩阵，策略一的平均总翻牌次数大于策略二的平均总翻牌次数，且记忆队列最大值和记忆时间越大，策略二优势越明显。当记忆队列最大值和记忆时间过小时，策略一优于策略二。这是由于记忆队列最大值和记忆时间过小，遗忘纸牌数增多，而策略二比策略一更易受遗忘纸牌数影响。由此可证明记忆队列最大值和记忆时间在正常区间内，对规模较小的翻牌游戏，策略二更优。

对于6*6的矩阵，规律与5*5的矩阵类似，在记忆队列最大值和记忆时间正常区间内，策略二也更优。同时可以看到，对于两种策略，随着记忆队列最大值和记忆时间的增大，翻牌的次数收敛。

 

10 模型改进

该游戏中，纸牌记忆属于短时记忆。根据干扰学说，遗忘是储存在短时记忆中的信息被其它信息干扰造成的。即信息的强度由于新信息进入短时记忆而减弱。短期记忆规律如图[1]：

以其中"每秒一个"的遗忘规律函数作为建模中记忆队列各纸牌的遗忘函数。每次翻牌与记忆队列各纸牌对比图案时，对于记忆队列的每张纸牌，取0-1之间的随机值，若该值小于该纸牌的遗忘函数值，则该纸牌能记起；否则，该纸牌被遗忘，从记忆队列中删除。

对游戏玩家的遗忘队列作如下修改:

,其中pro为0-1区间的随机数。

 

n大于12后可根据需求调整，如n=13时，=0。

 

 

 

11 总结

为获得优化的翻牌策略，即用尽可能少的翻牌次数完成游戏。问题的提出来源于生活的一个有趣细节，从中可见数学建模就在生活中。我们采用了常见的数据结构如队列和矩阵等对游戏进行建模分析，运用贪心法得出策略，并对策略进行优化。在对模型的分析中，同时考虑了人的短时记忆的因素。最后，我们通过编程对算法进行实现，通过大量实验验证了算法的有效性。

模型的不足之处在于，没有通过概率论等详细的计算分析优化算法。这里假设游戏玩家对纸牌的每一种图案的记忆能力是相同的，实际上对于人类的记忆来说，每一种图案的记忆能力，以及点击位置对图案的影响，以及遗忘规律都是非常复杂的，本文仅在一种简化的条件下进行分析研究，并给出建议，在实际游戏过程中的应用还需要进一步的研究。

 

12 参考文献

[1] Atkinson, R. C. & Shiffrin, R.M. (1968): Human memory: A proposed system and its control processes - In K.W. Spence & J.T. Spence（Eds.）,The Psychology of Learning and Motivation, Vol 2. London: Academic Press.

[2] Davelaar, E. J., Goshen-Gottstein, Y., A., A., Haarmann, H. J., & Usher, M. (2005): The demise of short-term memory revisited: empirical and computational investigation of recency effects. Psychological Review, 112, 3-42.

[3] 维基百科，短时记忆，http://zh.wikipedia.org/wiki/短时记忆，2014年7月13日

[4] 王晓东，计算机算法设计与分析（第4版），北京，电子工业出版社，2012.2

 

13 附录

 

1、算法1和算法2在6*6中表现图示

图5 算法1在6*6游戏中比较实验结果

 

图6 算法2在6*6游戏中比较实验结果

 

2、算法1和算法2具体数据

算法1：

表2 算法1实验结果（5*5）

时间（s）	5	6	7	8	9	10	11	12	13	14	15	16	18	20	1000
5	43.4	41.5	40.5	39.7	39.3	39.0	38.8	38.8	38.7	38.6	38.9	38.6	38.5	38.6	38.7
6	42.9	41.0	40.0	39.3	38.9	38.4	38.3	38.2	38。2	38.2	38.2	38.0	38.0	38.1	38.1
7	42.9	41.0	40.0	39.2	38.8	38.5	38.2	38.1	37.9	38.0	37.9	38.0	37.8	38.0	38.0
8	42.9	41.2	40.1	39.2	39.0	38.5	38.2	38.1	38.0	38.0	37.8	37.9	37.9	37.9	37.6
9	42,6	41,1	40.0	39.3	38.8	38.7	38.3	38.1	37.8	37.9	37.9	38.0	37.8	37.8	37.5
12	42.9	41.2	40.0	39.2	38.7	38.6	38.2	38.1	38.1	38.1	38.0	38.0	38.0	38.0	38.0
16	42.8	41.2	39.8	39.3	38.7	38.4	38.1	38.0	38.0	38.0	37.8	37.8	37.8	38.0	38.1
1000	43.1	41.3	39.8	39.2	39.0	38.3	38.2	38.0	38.1	38.1	37.9	37.9	37.8	37.9	37.9

 

表3 算法1实验结果（6*6）

时间（s）	5	6	7	8	9	10	11	12	13	14	15	16	18	20	1000
5	77.9	73.7	71.3	69.9	69.2	68.4	67.6	67.5	68.0	67.7	67.9	66.8	67.5	67。1	66.9
6	74.9	70.3	67.1	65.3	63.7	62.5	61.7	61.6	61.1	60.9	60.6	60.6	60.3	60.3	60.2
7	74.2	69.4	66.3	64.2	62.4	61.5	60.6	60.0	59.6	59.2	58.9	58.5	58.5	58.2	58.1
8	74.4	69.5	66.2	63.9	62.4	61.0	60.2	59.5	59.0	58.8	58.3	58.1	57.7	57,4	57.1
9	74.8	69.1	66.1	63.9	62,2	61,0	59.9	59.6	59.6	58.9	58.7	58.2	57.9	57.4	57.1
12	74.5	69.4	66.2	63.8	62.3	61.1	60.3	59.4	58.8	58.5	58.1	57.8	57.6	57.4	57.0
16	74.3	68.8	66.0	63.9	62.2	61.1	60.1	60.1	59.6	58.9	58.6	58.2	57.9	57,3	57.0
1000	74.2	68.7	65.0	63.6	62.1	61.1	60.1	60.0	595	58.4	58.5	57.6	57.4	57,3	57.1

 

算法2：

表4 算法2实验结果（5*5）

时间（s）	5	6	7	8	9	10	11	12	13	14	15	16	18	20	1000
5	43.6	41.5	41.1	40.1	39.5	39.4	39.2	39.4	38.9	38.9	39.0	39.0	39.0	39.0	39.0
6	43.1	41.1	40.0	39.1	38.5	38.1	37.9	37.6	37.7	37.6	37.6	37.5	37.5	37.4	37.5
7	43.1	41.2	39.7	38.9	38.3	37.8	37.6	37.5	37.3	37.0	37.1	37.0	37.2	36.9	37.1
8	42.9	41.1	39.9	38.9	38.3	37.7	37.6	37.3	37.1	36.9	36.8	36.9	36.9	36.9	36.7
9	43.0	40.9	39.6	38.8	38.1	37.7	37.4	37.2	37.0	36.9	36.8	36.8	36.8	36.7	36.9
12	42.7	40.8	39.7	38.9	38.2	37.8	37.5	37.3	36.9	36.9	37.0	36.7	36.8	36.8	36.8
16	43.0	41.0	39.8	38.7	38.3	37.9	37.5	37.2	37.0	36.9	36.9	36.9	36.8	36.7	36.9
12	42.9	40.9	39.5	38.9	38.2	37.8	37.4	37.1	37.1	36.9	36.8	36.8	36.9	36.8	36.8
16	42.8	40.9	39.5	38.8	38.1	37.7	37.2	37.1	36.9	37.0	36.9	37.0	36.8	36.7	36.8
1000	42.8	41.0	39.7	38.6	38.1	37.7	37.3	37.3	36.9	36.9	36.7	37.0	36.8	36.8	36.7

 

表5 算法2实验结果（6*6）

时间（s）	5	6	7	8	9	10	11	12	13	14	15	16	18	20	1000
5	81.2	76.9	74.4	72.7	72.7	72.3	71.7	71.9	71.6	70.8	70.8	71.1	71.1	71.3	71.3
6	77.1	71.3	68.3	66.1	64.8	64.2	63.7	63.6	62.4	62.7	62.2	62.9	62.7	62.6	62.2
7	76.2	70.5	66.8	64.5	62.9	61.9	60.9	60.3	60.0	59.5	59.4	59.1	58.8	59.0	58.8
8	76.3	70.1	66.4	63.9	62.2	61.0	60.0	59.4	59.0	58.4	58.2	57.7	57.3	57.3	57.2
9	76.0	70.3	66.5	63.9	62.0	60.8	59.6	59.0	58.4	57.8	57.5	57.2	56.8	56.5	56.5
16	75.8	70.2	66.4	63.8	62.1	60.6	59.5	58.8	58.1	57.7	57.2	56.8	56.2	56.1	55.9
1000	75.9	70.2	66.5	64.0	62.2	60.6	59.8	58.7	58.0	57.8	57.3	56.9	56.3	56.0	55.9

 

3、源程序

软件名称：code;;blocks 12.04 Mathematica 8.0.1

全部计算程序：

1.策略模拟

 

 

#include <stdio.h>

#include <stdlib.h>

#include <time.h>

#include <string.h>

#define max_int 100

int n;

int type;

int ta[max_int];

int stimes=0;

int c;

int msize;

struct memory

{

int x,y;//从零开始记

int num;

int ttl;

};

int todo;

int next;

struct memory mqueue[max_int*max_int];

int sm=0;

int em=0;

struct matrix

{

int done;

int times;

int num;

};

struct matrix x[max_int][max_int];

void print()

{

printf("\n mqueue: from %d to %d\n",em,sm);

for(int l=em; l<=sm; l++)

{

printf("%d ",mqueue[l].num);

}

printf("\nmatrix:\n");

for(int i=0; i<n; i++)

{

for(int j=0; j<n; j++)

{

printf("%d %d %d ",x[i][j].num,x[i][j].done,x[i][j].times);

}

printf("\n");

}

printf("ta:\n");

for(int i=1;i<=n;i++)

{

printf("%d ",ta[i]);

}

printf("\n");

}

void check()

{

//检查mqueue中需要去掉元素、ttl过期的元素、超出msize的元素

//print();

int cn=em;

for(int i=em; i<=sm; i++)

{

mqueue[i].ttl--;

if(mqueue[i].ttl<=0)

{

mqueue[i].num=-1;

}

if(mqueue[i].num!=-1)

{

mqueue[cn].x=mqueue[i].x;

mqueue[cn].y=mqueue[i].y;

mqueue[cn].num=mqueue[i].num;

mqueue[cn++].ttl=mqueue[i].ttl;

}

}

sm=cn-1;

if(sm-em+1>msize)

{

em=sm-msize+1;

}

//print();

}

void create()

{

int init[n*n];

int index=0;

int temp;

for(int i=1; i<=type; i++)

{

for(int j=0; j<4; j++)

{

init[index++]=i;

}

}

if(type*4!=n*n)

{

init[n*n-1]=0;

//printf("init boomb\n");

}

 

int temp1=0;

int temp2=0;

 

for(int i=0; i<1000; i++)

{

temp1=rand()%(n*n);

temp2=rand()%(n*n);

//printf("temp1:%dtemp2:%d\n",temp1,temp2);

temp=init[temp1];

init[temp1]=init[temp2];

init[temp2]=temp;

}

index=0;

 

for(int i=0; i<n; i++)

{

for(int j=0; j<n; j++)

{

x[i][j].num=init[index++];

x[i][j].done=0;

x[i][j].times=0;

}

}

}

void stategy1()

{

//初始化block队列相关

stimes=0;

mqueue[0].x=-1;

mqueue[0].y=-1;

mqueue[0].num=-1;

todo=n*n;

next=0;

em=0;

sm=0;

for(int i=1;i<=n;i++)

ta[i]=4;

 

 

while(todo>0)//已经没了直接跳出

{

//printf("todo:%d\n",todo);

//system("pause");

int mark=0;

//这里首先检查有没有记忆中两次相同的（偶数次点击）

if(sm-em>=1)

{

for(int i=em; i<=sm-1; i++)

{

for(int j=i+1; j<=sm; j++)

{

if(mqueue[i].num==mqueue[j].num)

{

stimes=stimes+2;

todo=todo-2;

mqueue[i].num=-1;

mqueue[j].num=-1;

x[mqueue[i].x][mqueue[i].y].times++;

x[mqueue[i].x][mqueue[i].y].done=1;

x[mqueue[j].x][mqueue[j].y].times++;

x[mqueue[j].x][mqueue[j].y].done=1;

i=sm;

mark=1;

break;

 

}

}

}

 

if(mark==1)

{time_t t;

//printf("continue from same appears in memory\n");

check();

continue;

}

 

}

 

 

//模拟点击两次的动作，按照顺序点击

 

int cc=next;

int cc2;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc%(n*n))/n][(cc%(n*n))%n].times++;

 

//首先看是不是鬼牌，如果是的话则直接消去下一个以及下一个相同的。

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==0)

{

 

cc2=next;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].times++;

 

for(int i=n-1; i>=0; i--)

{

for(int j=n-1; j>=0; j--)

{

if(x[i][j].num==x[(cc2%(n*n))/n][(cc2%(n*n))%n].num)

{

todo=todo-3;

x[i][j].done=1;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].done=1;

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

i=-1;

break;

}

}

}

//printf("0 boomb!\n");

check();

continue;

 

}

//进入memory查找

for(int i=em; i<=sm; i++)

{

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==mqueue[i].num)

{

//printf("found in memory\n");

mqueue[i].num=-1;//如果找到了memory直接消掉

//接下来针对matrix处理

stimes++;

x[mqueue[i].x][mqueue[i].y].done=1;

x[mqueue[i].x][mqueue[i].y].times++;

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

todo=todo-2;

mark=1;

break;

}

}

 

//那如果找不到呢，点击第二张

//

if(mark==1)

{

//printf("continue from found in memory\n");

check();

continue;

}

 

cc2=next;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].times++;

//相同直接消去，不相同加入memory

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==x[(cc2%(n*n))/n][(cc2%(n*n))%n].num)

{

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].done=1;

todo=todo-2;

//printf("same,yeah!\n");

check();

}

else

{

mqueue[++sm].num=x[(cc%(n*n))/n][(cc%(n*n))%n].num;

mqueue[sm].x=(cc%(n*n))/n;

mqueue[sm].y=(cc%(n*n))%n;

mqueue[sm].ttl=c;

mqueue[++sm].num=x[(cc2%(n*n))/n][(cc2%(n*n))%n].num;

mqueue[sm].x=(cc2%(n*n))/n;

mqueue[sm].y=(cc2%(n*n))%n;

mqueue[sm].ttl=c;

//printf("not same\n");

check();

}

}

return;

}

void stategy2()

{

//初始化block队列相关

stimes=0;

mqueue[0].x=-1;

mqueue[0].y=-1;

mqueue[0].num=-1;

todo=n*n;

next=0;

em=0;

sm=0;

for(int i=1;i<=n;i++)

ta[i]=4;

 

while(todo>0)//已经没了直接跳出

{

//printf("todo:%d\n",todo);

//system("pause");

int mark=0;

//这里首先检查有没有记忆中两次相同的（偶数次点击）

if(sm-em>=1)

{

for(int i=em; i<=sm-1; i++)

{

for(int j=i+1; j<=sm; j++)

{

if(mqueue[i].num==mqueue[j].num&&ta[mqueue[i].num]<=2)

{

stimes=stimes+2;

todo=todo-2;

ta[mqueue[i].num]-=2;

mqueue[i].num=-1;

mqueue[j].num=-1;

x[mqueue[i].x][mqueue[i].y].times++;

x[mqueue[i].x][mqueue[i].y].done=1;

x[mqueue[j].x][mqueue[j].y].times++;

x[mqueue[j].x][mqueue[j].y].done=1;

i=sm;

mark=1;

break;

 

}

}

}

 

if(mark==1)

{time_t t;

//printf("continue from same appears in memory\n");

check();

continue;

}

 

}

 

 

//模拟点击两次的动作，按照顺序点击

 

int cc=next;

int cc2;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc%(n*n))/n][(cc%(n*n))%n].times++;

 

//首先看是不是鬼牌，如果是的话则直接消去下一个以及下一个相同的。

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==0)

{

 

cc2=next;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].times++;

 

for(int i=n-1; i>=0; i--)

{

for(int j=n-1; j>=0; j--)

{

if(x[i][j].num==x[(cc2%(n*n))/n][(cc2%(n*n))%n].num)

{

todo=todo-3;

x[i][j].done=1;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].done=1;

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

ta[x[i][j].num]-=2;

i=-1;

break;

}

}

}

//printf("0 boomb!\n");

check();

continue;

 

}

//进入memory查找

for(int i=em; i<=sm; i++)

{

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==mqueue[i].num)

{

//printf("found in memory\n");

ta[mqueue[i].num]-=2;

mqueue[i].num=-1;//如果找到了memory直接消掉

//接下来针对matrix处理

stimes++;

x[mqueue[i].x][mqueue[i].y].done=1;

x[mqueue[i].x][mqueue[i].y].times++;

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

todo=todo-2;

mark=1;

break;

}

}

 

//那如果找不到呢，点击第二张

//

if(mark==1)

{

//printf("continue from found in memory\n");

check();

continue;

}

 

cc2=next;

next++;

while(x[(next%(n*n))/n][(next%(n*n))%n].done!=0)

{

next++;

}

stimes++;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].times++;

//相同直接消去，不相同加入memory

if(x[(cc%(n*n))/n][(cc%(n*n))%n].num==x[(cc2%(n*n))/n][(cc2%(n*n))%n].num)

{

x[(cc%(n*n))/n][(cc%(n*n))%n].done=1;

x[(cc2%(n*n))/n][(cc2%(n*n))%n].done=1;

ta[x[(cc%(n*n))/n][(cc%(n*n))%n].num]-=2;

todo=todo-2;

//printf("same,yeah!\n");

check();

}

else

{

mqueue[++sm].num=x[(cc%(n*n))/n][(cc%(n*n))%n].num;

mqueue[sm].x=(cc%(n*n))/n;

mqueue[sm].y=(cc%(n*n))%n;

mqueue[sm].ttl=c;

mqueue[++sm].num=x[(cc2%(n*n))/n][(cc2%(n*n))%n].num;

mqueue[sm].x=(cc2%(n*n))/n;

mqueue[sm].y=(cc2%(n*n))%n;

mqueue[sm].ttl=c;

//printf("not same\n");

check();

}

}

return;

}

int main()

{

//首先规定大小生成矩阵，其中参数为4*x+n*n-4*x

//freopen("output.txt","w+",stdout);

time_t t;

srand((unsigned) time(&t));

scanf("%d",&n);

printf("\nn:%d \n",n);

type=n*n/4;

int s=0;

for(int i=0; i<1000; i++)

{

create();

//print();

//printf("please input c and msize");

//scanf("%d%d",&c,&msize);

c=2000;

msize=7;

stategy2();

//print();

printf("times:%d\n",stimes);

s+=stimes;

}

printf("sum :%d\n",s);

return 0;

}

 

2.绘图

data1 = {

{43.4, 41.5, 40.5, 39.7, 39.3, 39.0, 38.8, 38.8, 38.7, 38.6, 38.9,

38.6, 38.5, 38.6, 38.7},

{42.9, 41.0, 40.0, 39.3, 38.9, 38.4, 38.3, 38.2, 38.2, 38.2, 38.2,

38.0, 38.0, 38.1, 38.1},

{42.9, 41.0, 40.0, 39.2, 38.8, 38.5, 38.2, 38.1, 37.9, 38.0, 37.9,

38.0, 37.8, 38.0, 38.0},

{42.9, 41.2, 40.1, 39.2, 39.0, 38.5, 38.2, 38.1, 38.0, 38.0, 37.8,

37.9, 37.9, 37.9, 37.6},

{42.6, 41.1, 40.0, 39.3, 38.8, 38.7, 38.3, 38.1, 37.8, 37.9, 37.9,

38.0, 37.8, 37.8, 37.5},

{42.9, 41.2, 40.0, 39.2, 38.7, 38.6, 38.2, 38.1, 38.1, 38.1, 38.0,

38.0, 38.0, 38.0, 38.0},

{42.8, 41.2, 39.8, 39.3, 38.7, 38.4, 38.1, 38.0, 38.0, 38.0, 37.8,

37.8, 37.8, 38.0, 38.1},

{43.1, 41.3, 39.8, 39.2, 39.0, 38.3, 38.2, 38.0, 38.1, 38.1, 37.9,

37.9, 37.8, 37.9, 37.9}};

a=ListPlot3D[data1,PlotStyle->RGBColor[255,0,0]];

data2 = {{43.5, 41.8, 40.6, 40.0, 39.7, 39.3, 39.1, 39.2, 39.0, 39.1,

38.9, 39.0, 38.8, 39.2, 38.9, 39.2},

{42.9, 41.1, 40.0, 38.9, 38.6, 38.2, 37.9, 37.7, 37.6, 37.5, 37.6,

37.5, 37.6, 37.5, 37.6, 37.4},

{42.8, 41.0, 39.8, 38.8, 38.2, 37.9, 37.5, 37.4, 37.1, 37.2, 36.8,

37.0, 37.1, 37.1, 37.1, 37.2},

{42.9, 41.2, 39.4, 38.7, 38.3, 37.7, 37.3, 37.0, 37.0, 37.0, 36.9,

36.8, 36.8, 36.9, 36.8, 36.8},

{42.9, 40.9, 39.5, 38.9, 38.1, 37.8, 37.4, 37.2, 37.2, 36.8, 36.8,

36.9, 36.9, 36.8, 36.7, 36.8},

{43.3, 41.1, 39.7, 38.8, 38.2, 37.7, 37.4, 37.1, 37.0, 36.9, 36.8,

36.8, 36.8, 36.7, 36.9, 36.8},

{43.1, 41.0, 39.6, 38.6, 38.3, 37.6, 37.5, 37.2, 37.1, 36.8, 36.9,

36.8, 36.7, 36.8, 36.8, 36.7},

{43.2, 40.9, 39.6, 38.9, 38.2, 37.6, 37.4, 37.1, 37.0, 37.0, 36.8,

36.6, 36.7, 36.8, 36.8, 36.8},

{42.9, 40.7, 39.6, 38.7, 38.2, 37.8, 37.5, 37.1, 37.0, 37.0, 36.9,

36.9, 36.8, 36.8, 36.7, 36.9},

{42.8, 41.0, 39.5, 38.9, 38.2, 37.7, 37.5, 37.1, 37.0, 36.9, 36.9,

36.7, 36.8, 36.9, 36.7, 36.9},

{43.2, 40.9, 39.8, 38.9, 38.1, 37.6, 37.4, 37.1, 36.8, 36.9, 36.8,

36.8, 36.9, 36.8, 36.9, 36.8},

{43.2, 40.9, 39.5, 38.9, 38.1, 37.9, 37.5, 37.3, 37.0, 37.0, 36.8,

36.8, 36.9, 37.0, 36.8, 36.8},

{42.8, 40.9, 39.8, 38.7, 38.2, 37.7, 37.4, 37.3, 36.9, 36.8, 36.8,

36.9, 36.9, 36.9, 36.8, 36.8},

{42.9, 41.1, 39.7, 38.8, 38.1, 37.8, 37.4, 37.2, 37.1, 37.0, 36.8,

36.8, 36.8, 36.9, 36.8, 36.8},

{43.1, 40.9, 39.6, 38.8, 38.1, 37.8, 37.4, 37.1, 37.0, 36.9, 36.9,

36.8, 36.9, 36.7, 36.8, 36.8},

{43.0, 41.0, 39.7, 38.8, 38.2, 37.8, 37.4, 37.1, 36.9, 36.8, 36.9,

36.8, 36.8, 36.9, 37.0, 36.7}};

b = ListPlot3D[data2];

Show[a, b, PlotRange -> All];

data3 = {{78.0, 73.9, 71.6, 70.2, 68.7, 67.8, 68.0, 68.0, 67.3, 67.6,

67.6, 67.7, 67.5, 67.5, 67.7, 67.5},

{74.6, 70.1, 66.9, 65.1, 63.6, 62.7, 61.8, 61.2, 60.9, 60.8, 60.7,

60.6, 60.3, 60.4, 60.3, 60.1},

{74.5, 69.4, 66.3, 64.2, 62.5, 61.5, 60.6, 60.0, 59.5, 59.1, 58.8,

58.7, 58.5, 58.3, 58.2, 58.0},

{74.8, 69.3, 66.1, 64.0, 62.4, 61.1, 60.2, 59.5, 59.1, 58.6, 58.2,

58.2, 57.8, 57.6, 57.4, 57.4},

{74.5, 69.4, 66.3, 64.2, 62.3, 61.1, 60.1, 59.5, 58.9, 58.7, 58.3,

57.9, 57.9, 57.5, 57.4, 57.4},

{74.6, 69.3, 66.2, 64.1, 62.2, 61.2, 60.0, 59.6, 58.9, 58.4, 58.1,

57.9, 57.8, 57.4, 57.4, 57.2},

{74.3, 69.5, 66.2, 64.2, 62.3, 61.2, 60.2, 59.8, 58.9, 58.7, 58.2,

58.0, 57.7, 57.4, 57.4, 57.3},

{74.5, 69.6, 66.1, 64.0, 62.4, 61.1, 60.2, 59.5, 58.9, 58.5, 58.2,

57.9, 57.6, 57.6, 57.4, 57.2},

{74.2, 69.2, 66.1, 64.0, 62.1, 61.0, 60.1, 59.6, 59.0, 58.5, 58.2,

57.9, 57.6, 57.5, 57.5, 57.2},

{74.5, 69.4, 66.2, 64.1, 62.2, 60.9, 60.0, 59.4, 59.0, 58.5, 58.2,

57.9, 57.7, 57.6, 57.4, 57.3},

{74.1, 69.5, 66.3, 64.0, 62.1, 60.9, 60.2, 59.5, 59.1, 58.6, 58.2,

58.0, 57.7, 57.5, 57.5, 57.2},

{74.4, 69.5, 66.3, 63.8, 62.3, 61.1, 60.4, 59.4, 59.1, 58.5, 58.2,

57.8, 57.6, 57.4, 57.2, 57.2},

{74.5, 69.2, 66.4, 64.0, 62.3, 61.0, 60.3, 59.4, 59.1, 58.6, 58.3,

58.0, 57.6, 57.4, 57.4, 57.2},

{74.4, 69.4, 66.3, 64.1, 62.3, 61.1, 60.1, 59.5, 58.9, 58.5, 58.2,

57.9, 57.9, 57.5, 57.4, 57.2},

{74.4, 69.4, 66.2, 63.9, 62.5, 61.1, 60.3, 59.4, 59.1, 58.6, 58.3,

58.0, 57.7, 57.5, 57.2, 57.3},

{74.5, 69.4, 66.3, 64.0, 62.4, 61.1, 60.3, 59.5, 59.1, 58.5, 58.1,

58.0, 57.8, 57.5, 57.4, 57.3}};

data4 = {{81.5, 77.1, 74.2, 72.4, 72.7, 72.0, 71.8, 70.9, 71.6, 71.8,

71.3, 71.6, 70.2, 71.0, 72.0, 71.7},

{76.7, 71.1, 68.6, 66.2, 65.1, 64.2, 63.2, 63.3, 62.6, 62.1, 62.8,

62.3, 62.4, 62.1, 62.1, 62.4},

{76.5, 70.8, 67.0, 64.6, 62.8, 61.9, 61.2, 60.6, 59.8, 59.7, 59.4,

59.3, 59.0, 58.9, 58.9, 58.9},

{76.0, 69.9, 66.6, 64.0, 62.1, 60.8, 60.3, 59.2, 58.8, 58.2, 58.1,

57.9, 57.6, 57.4, 57.2, 57.0},

{76.0, 70.1, 66.2, 63.9, 62.1, 60.7, 59.7, 59.0, 58.4, 57.8, 57.5,

57.1, 56.9, 56.6, 56.6, 56.3},

{76.1, 69.7, 66.4, 63.9, 61.9, 60.6, 59.6, 58.9, 58.3, 57.7, 57.2,

57.0, 56.7, 56.5, 56.1, 56.0},

{75.9, 69.9, 66.7, 64.0, 62.1, 60.5, 59.6, 58.7, 58.4, 57.6, 57.2,

56.9, 56.7, 56.3, 56.0, 55.9},

{75.9, 70.4, 66.4, 63.8, 61.9, 60.7, 59.5, 58.8, 58.0, 57.7, 57.3,

56.9, 56.4, 56.3, 56.0, 55.8},

{76.0, 69.9, 66.4, 63.9, 61.9, 60.5, 59.6, 58.8, 58.1, 57.7, 57.1,

56.8, 56.5, 56.3, 56.0, 56.0},

{76.0, 70.2, 66.3, 63.8, 62.0, 60.4, 59.6, 58.8, 58.1, 57.7, 57.1,

57.0, 56.5, 56.3, 56.2, 55.9},

{76.2, 70.5, 66.2, 63.8, 62.0, 60.5, 59.7, 58.8, 58.2, 57.6, 57.2,

56.8, 56.5, 56.2, 56.0, 55.8},

{76.6, 70.4, 66.5, 63.9, 61.9, 60.7, 59.4, 58.6, 58.3, 57.8, 57.2,

56.9, 56.5, 56.1, 56.1, 55.7},

{76.2, 70.0, 66.4, 63.8, 62.1, 60.7, 59.7, 58.8, 58.1, 57.7, 57.1,

56.8, 56.5, 56.3, 56.0, 56.1},

{76.2, 70.2, 66.5, 63.9, 62.1, 60.3, 59.4, 58.8, 58.1, 57.7, 57.3,

56.6, 56.5, 56.1, 56.1, 55.7},

{76.2, 70.0, 66.4, 63.9, 62.0, 60.6, 59.4, 58.8, 58.0, 57.6, 57.2,

56.8, 56.5, 56.3, 56.1, 56.0},

{75.9, 70.0, 66.2, 63.9, 62.1, 60.4, 59.5, 58.7, 58.1, 57.6, 57.3,

56.9, 56.5, 56.2, 56.1, 55.9}};

c = ListPlot3D[data3, PlotStyle -> RGBColor[255, 0, 0]];

;

Show[c, d, PlotRange -> All];