【算法设计与分析】排序算法性能分析
github:项目地址
一、实验目的
- 掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理
- 掌握不同排序算法时间效率的经验分析方法,验证理论分析与经验分析的一致性。
二、实验概述
排序问题要求我们按照升序排列给定列表中的数据项,目前为止,已有多种排序算法提出。本实验要求掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理,并进行代码实现。通过对大量样本的测试结果,统计不同排序算法的时间效率与输入规模的关系,通过经验分析方法,展示不同排序算法的时间复杂度,并与理论分析的基本运算次数做比较,验证理论分析结论的正确性。
三、实验内容
-
实现选择排序、冒泡排序、合并排序、快速排序、插入排序算法;
-
以待排序数组的大小n为输入规模,固定n,随机产生20组测试样本,统计不同排序算法在20个样本上的平均运行时间;
-
分别以n=10000, n=20000, n=30000, n=40000, n=50000等等,重复2的实验,画出不同排序算法在20个随机样本的平均运行时间与输入规模n的关系,如下图1所示;

-
画出理论效率分析的曲线和实测的效率曲线,注意:由于实测效率是运行时间,而理论效率是基本操作的执行次数,两者需要进行对应关系调整。调整思路:以输入规模为10000的数据运行时间为基准点,计算输入规模为其他值的理论运行时间,画出不同规模数据的理论运行时间曲线,并与实测的效率曲线进行比较。经验分析与理论分析是否一致?如果不一致,请解释存在的原因。
-
现在有10亿的数据(每个数据四个字节),请快速挑选出最大的十个数,并在小规模数据上验证算法的正确性。
四、实验过程及分析
(一) 五种排序算法性能分析
1. 选择排序
a)基本算法
i.算法原理
①首先在未排序序列中找到最小元素,存放到排序序列的起始位置
②从剩余未排序元素中继续寻找最小元素,放到已排序序列的末尾。
③重复上述过程直至所有元素均排序完毕。
ii.伪代码
SELECTSORT ( L)
For i = 1 to L.length
minPos = selectMinKey(L, i) // 从i到末尾选择最小元素位置
If ( i != minPos)
Swap(L.r[i], L.r[minPos]) // 交换元素
iii.复杂度分析
需要遍历数组才能找到峰值元素,所以复杂度与原始序列是否有序无关,最好最坏和平均情况的时间复杂度都为 O ( n 2 ) O(n^2) O(n2);
需要一个临时变量用来交换数组内数据位置,所以空间复杂度为 O ( 1 ) O(1) O(1)。
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为10000)。理论值计算方法如下:
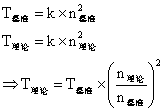
最终通过选择排序进行排序,最终结果如下:
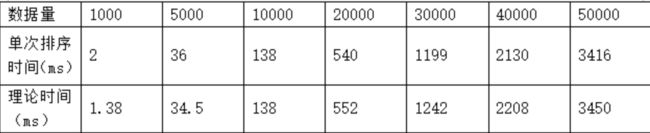
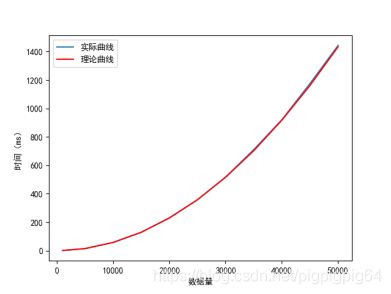
图像上符合 O ( n 2 ) O(n^2) O(n2) 二次曲线,并且理论值与实际值误差较小。
b) 优化算法
i.算法原理
①首先在未排序序列中找到最小、最大元素,存放到排序序列的起始、末尾位置
②从剩余未排序元素中继续寻找最小、最大元素,将最小元素放到已排序升序序列 的末尾,将最大元素放到已排序降序序列的起始。
③重复上述过程直至所有元素均排序完毕。
ii.伪代码
SELECTSORT ( L)
For i = 1 to L.length, k = L.length to 1
minPos = selectMinKey(L, i) // 从i到末尾选择最小元素位置
maxPos = selectMaxKey(L, i) // 从i到末尾选择最大元素位置
If ( i != minPos)
Swap(L.r[i], L.r[minPos]) // 交换元素
If ( max == i) maxPos = minPos // 防止之前的被换掉
If ( k - 1 != maxPos)
Swap(L.r[k - 1], L.r[maxPos]) // 交换元素
iii.复杂度分析
需要遍历数组才能找到峰值元素,所以复杂度与原始序列是否有序无关,最好最坏和平均情况的时间复杂度都为 O ( n 2 ) O(n^2) O(n2)。
需要一个临时变量用来交换数组内数据位置,所以空间复杂度为 O ( 1 ) O(1) O(1)。
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为10000)。理论值计算方法如下:
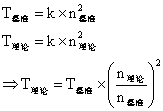
最终通过选择排序进行排序,最终结果如下:

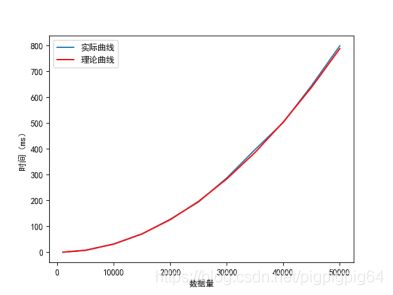
图像上符合 O ( n 2 ) O(n^2) O(n2) 二次曲线,并且理论值与实际值误差较小。
c) 综合分析
优化方法相对于原始方法,比较次数与交换次数不变,但是每一次对于未排序数组的遍历都可以一次找到最大最小值,所以可以减少一半的循环次数,在时间上进行优化。
优化前后数据、曲线如下:

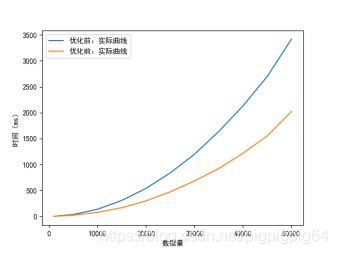
可以看到,时间接近减少了一半,与理论分析一致。
2. 冒泡排序
a)基本算法
i.算法原理
①比较相邻的元素。如果第一个比第二个大,就交换他们两个。
②对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
③针对所有的元素重复以上的步骤,除了最后一个。
④持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
ii.伪代码
BUBBLESORT (L)
For i = 1 to L.length
For j = i to L.length - 1
If (L.r[j] < L.r[j - 1])
Swap (L.r[j], L.r[j - 1]) // 交换元素
iii.复杂度分析
很明显,冒泡排序最好情况是数组已经有序的情况,此时只需要遍历一次数据,没有交换发生,结束排序,时间复杂度为 O ( n ) O(n) O(n)
最坏情况下的冒泡就是逆序,此时你需要遍历n-1次数据,此时的时间复杂度为 O ( n 2 ) O(n^2) O(n2)
平均情况下也为 O ( n 2 ) O(n^2) O(n2) 需要注意的是平均情况并不是与最坏情况下的时间复杂度相等。
只需要一个temp临时变量来交换数据,所以空间复杂度使 O ( 1 ) O(1) O(1)。
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为20000)。理论值计算方法如下:
最终通过选择排序进行排序,最终结果如下:
最终通过选择排序进行排序,最终结果如下:
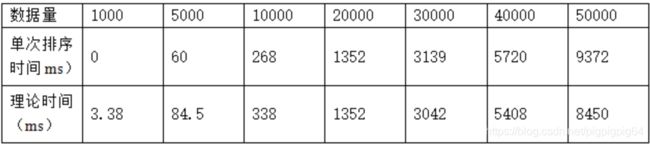

图像上符合 O ( n 2 ) O(n^2) O(n2) 二次曲线,并且理论值与实际值误差较小。
b) Flag标志位优化
i.算法原理
① 设置flag标志位,如果已经未发生交换说明已经有序,则跳出循环。
ii.伪代码
BUBBLESORT (L)
For i = 1 to L.length
Flag = True
For j = i to L.length - 1
If (L.r[j] < L.r[j - 1])
Swap (L.r[j], L.r[j - 1]) // 交换元素
Flag = True
If ( Flag == False)
break
iii.复杂度分析
与基本原理相同,只是加入了提前跳出循环的条件。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为20000)。理论值计算方法如下:
最终通过选择排序进行排序,最终结果如下:

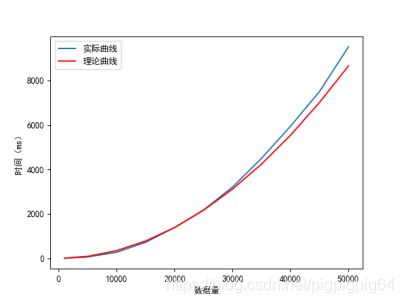
图像上符合O(n^2) 二次曲线,并且理论值与实际值误差较小。
c) 双向冒泡优化
i.算法原理
在基础算法的基础上进行优化。
首先从前往后把最大数移到最后,然后反过来从后往前把最小的一个数移动到数组最前面。
重复这一过程,最终就会把整个数组从小到大排列好。
ii.伪代码
BUBBLESORT (L)
forward_pos_temp = 0; // 记录前向最后一次交换的位置
forward_pos_cur = L.length - 1; // 当前需要冒泡的前向截止位置
reverse_pos_temp = 0; // 记录前向最后一次交换的位置
reverse_pos_cur = 0; // 当前需要冒泡的后向截止位置
For i = 1 to L.length
Flag = False
For j = 0 to forward_pos_cur
// 当前比后面的值大,则冒泡到后面去
If (L.r[j] > L.r[j + 1])
Swap (L.r[j], L.r[j + 1]) // 交换元素
Flag = True
If ( Flag == False) break
forward_pos_cur = forward_pos_temp
For j = forward_pos_cur to reverse_pos_cur step = -1
// 当前比前面的值小,则冒泡到前面去
If (L.r[j] < L.r[j - 1])
Swap (L.r[j], L.r[j + 1]) // 交换元素
Flag = True
If ( Flag == False) break
reverse_pos_cur = reverse_pos_temp
iii.复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为20000)。理论值计算方法如下:
最终通过选择排序进行排序,最终结果如下:

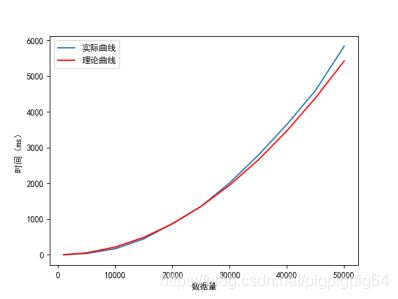
图像上符合 O ( n 2 ) O(n^2) O(n2)二次曲线,并且理论值与实际值误差较小。
d) 综合分析
优化前后数据、曲线如下:
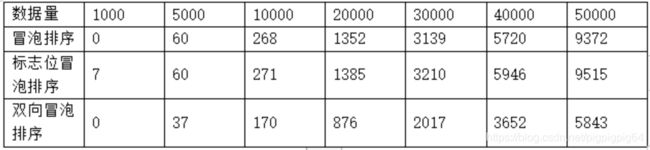
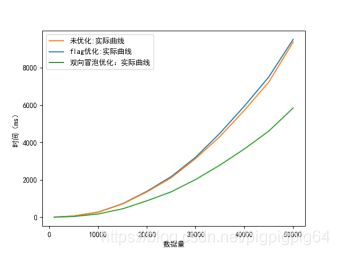
从图中可以看出,flag标志位的设置对于排序优化影响不大,反而性能更慢。
经分析,原因是flag标志位的设置,对相对有序序列的影响较大。实验数据集为完全均分分布随机数列。完全随机数列有序可能性极低,而对于flag标志位的判断语句反而使排序更慢。
相对而言,双向冒泡排序对于性能的提升较大。双向排序时数组的两头都排序好了,我们只需要处理数组的中间部分即可。单向即传统的冒泡排序只有尾部的元素是排好序的,每轮处理都需要从头一直处理到已经排好序元素的前面一个元素。
我对于元素比较次数/交换次数进行了统计,如下图:
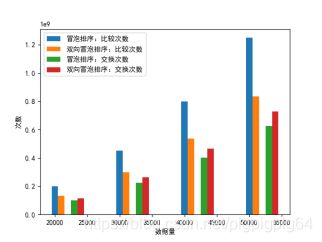
可以看到,双向冒泡排序在比较次数上减少,交换次数增多。
3. 插入排序
a) 基本算法
i.算法原理
①将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
②从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。
ii.伪代码
INSERTSORT (L)
For i = 1 to L.length
For j = i to 0
If ( L.r[j] < L.r[j -1])
Swap (L.r[j], L.r[j -1])
Else
break
iii.复杂度分析
时间复杂度:需要首先遍历数组,然后在已排序数组中查找插入的位置。所以时间复杂度为 O ( n 2 ) O (n^2) O(n2)。
空间复杂度:需要一个临时变量用于交换元素,所以空间复杂度为 O ( 1 ) O (1) O(1)。
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为10000)。理论值计算方法如下:
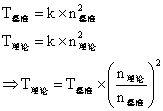
最终通过选择排序进行排序,最终结果如下:
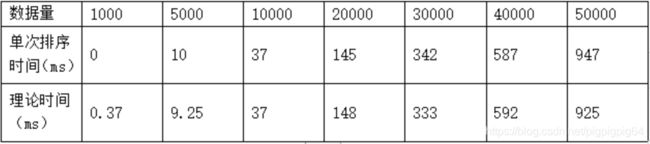

图像上符合O(n^2) 二次曲线,并且理论值与实际值误差较小。
b)优化算法
i.算法原理
在原来原算法的基础上进行优化
将直接交换替换成赋值
ii.伪代码
INSERTSORT (L)
For i = 1 to L.length
E = L.r[i]
For j = i to 0 and L.r[j - 1] > E
L.r[j] = L.r[j -1]
L.r[j] = E
iii.复杂度分析
时间复杂度: O ( n 2 ) O (n^2) O(n2)
空间复杂度: O ( 1 ) O (1) O(1)
iv.数据测试
使用随机数生成,均匀分布的生成了1000~50000的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为10000)。理论值计算方法如下:

最终通过选择排序进行排序,最终结果如下:

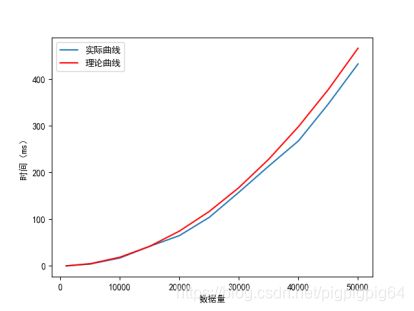
图像上符合 O ( n 2 ) O(n^2) O(n2)二次曲线,并且理论值与实际值误差较小。
c)综合分析
优化前后数据、曲线如下:

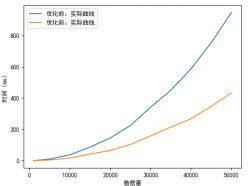
从图中可以看出,用赋值语句替代交换语句效率提升明显。
原因是交换语句相较赋值语句更为复杂,且引入了中间变量。不再频繁使用交换函数,赋值比交换函数运行速度更快。
4. 归并排序
a) 基本算法
i.算法原理
① 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
② 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
③ 重复步骤 3 直到某一指针达到序列尾;
④ 将另一序列剩下的所有元素直接复制到合并序列尾。
ii.伪代码
MERGESORT (L, front, end)
If (front >= end) return
Mid = (front + end) / 2
MERGESORT (L, front, mid)
MERGESORT(L, mid + 1, end)
Merge (L, front, mid, end) // 将front—mid,mid+1—end合并
iii.复杂度分析
时间复杂度分析:递归分解数据,每次都需要分成两组,对n个数据扫描一次。
可以获得如下递推公式: T ( n ) = 2 T ( n / 2 ) + O ( n ) , T ( 1 ) = 1 T(n) = 2T(n/2) + O(n), T(1) = 1 T(n)=2T(n/2)+O(n),T(1)=1
经过数学推导可得 T ( n ) = n + n l o g ( n ) T(n) = n + nlog(n) T(n)=n+nlog(n)
所以时间复杂度为 O ( n l o g n ) O (nlogn) O(nlogn)
空间复杂度分析:归并排序需要一个临时temp[ ]来储存归并的结果,所以 O ( n ) O(n) O(n)
iv.数据测试
使用随机数生成,均匀分布的生成了 1 0 5 10^5 105 ~ 5 ∗ 1 0 7 5*10^7 5∗107 的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为 1 0 5 10^5 105)。理论值计算方法如下:
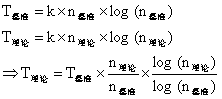
最终通过选择排序进行排序,最终结果如下:
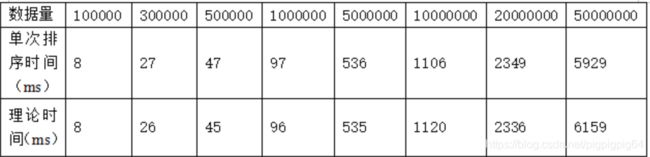

图像上符合 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n)) 二次曲线,并且理论值与实际值误差较小。
b) 综合分析
归并排序利用了分治法的思路,将大问题分解为了两个小问题,极大程度上提升了排序算法的效率,将时间复杂度降到了 O ( n l o g n ) O(nlogn) O(nlogn),但是由于需要引入临时数组存放合并数组,所以在空间上不够高效。
5. 快速排序
a)基本算法
i.算法原理
① 从数列中挑出一个元素,称为 “基准”
② 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作
③ 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序;
ii.伪代码
QUICKSORT(L, low, high)
if (low < high)
pivot = PARTITON(A, low, high)
QUICKSORT(A, low, pivot - 1)
QUICKSORT(A, pivot + 1, high)
PARTITION(L, low, high)
pivot = L.r[low];
while (low < high)
while (low < high && L.r[high] >= pivot)
high --
L.r[low] = L.r[high]
while (low < high && L.r[low] <= pivot)
low ++
L.r[high] = L.r[low]
L.r[low] = pivot
return low
iii.复杂度分析
时间复杂度分析: 快速排序的一次划分算法从两头交替搜索,直到 low 和 hight 重合,因此其时间复杂度是 O ( n ) O(n) O(n)。整个快速排序算法的时间复杂度与划分的趟数有关。最理想的情况是,每次划分所选择的中间数恰好将当前序列几乎等分,经过 logn趟划分,便可得到长度为 1 的子表。这样,整个算法的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
iv.数据测试
使用随机数生成,均匀分布的生成了 1 0 5 10^5 105 ~ 5 ∗ 1 0 7 5*10^7 5∗107 的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
为了检验实验是否准确,将实际值将理论值进行对比(基准点为10^5)。理论值计算方法如下:
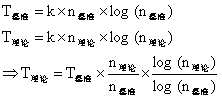
最终通过选择排序进行排序,最终结果如下:
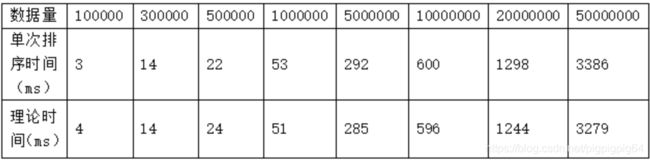
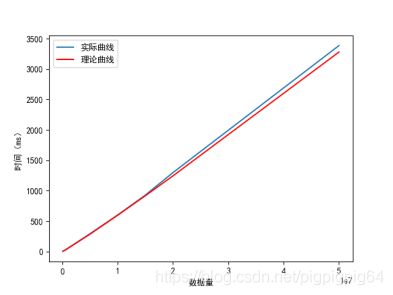
图像上符合 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n)) 二次曲线,并且理论值与实际值误差较小。
b)综合分析
归并排序利用了分治法的思路,将大问题分解为了两个小问题,极大程度上提升了排序算法的效率,将时间复杂度降到了 O ( n l o g n ) O(nlogn) O(nlogn)。
6. 总体分析
本次测试的五种排序算法可以分为两类:
时间复杂度 O ( n 2 ) O (n^2) O(n2):选择排序、冒泡排序、插入排序
时间复杂度 O ( n l o g n ) O (nlogn) O(nlogn):归并排序、快速排序
二者在大数据测试中,时间效率上不在一个量级, O ( n l o g n ) O (nlogn) O(nlogn)算法明显大幅度领先于 O ( n 2 ) O (n^2) O(n2)算法。所以不在同一张图表中进行比较,将对二者分别进行分析。
首先是 O ( n 2 ) O (n^2) O(n2)排序算法的分析:

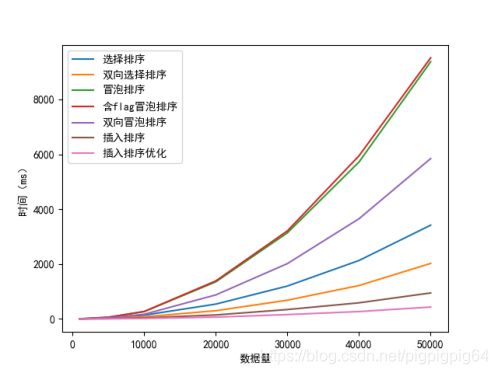
由图表中我们可以看出总体上来说:插入排序 < 选择排序 < 冒泡排序
① 冒泡排序存在大量判断、交换语句,并且有许多冗余操作。所以效率相对较低。
② 插入排序与选择排序相近,每一趟内循环,都能准确的确定一个元素的位置。所以时间效率取决与序列的有序程度。
接下来是 O ( n l o g n ) O (nlogn) O(nlogn)排序算法的分析:

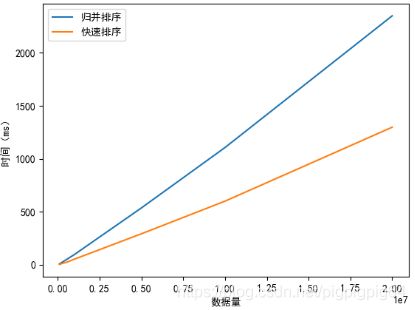
由图表中我们可以看出总体上来说:快速排序 < 归并排序
归并排序相对于快速排序,需要多次开辟内存空间进行数组的合并操作,在一定程度上降低了算法的效率,所以在速度上慢于快速排序。
(二) TopK问题分析
10亿数据属于大数据,利用 O ( n 2 ) O(n^2) O(n2)的复杂度去查找效率很低,又需要遍历全序列所以一定大于 O ( n ) O(n) O(n)。
可知 O ( 1 ) < O ( l o g n ) < O ( n ) < O ( k n ) < O ( n l o g n ) < O ( n 2 ) < O ( n 3 ) O(1) < O(logn) < O(n) < O(kn) < O(nlogn) < O(n^2) < O(n^3) O(1)<O(logn)<O(n)<O(kn)<O(nlogn)<O(n2)<O(n3)
所以本次实验选择介于 O ( n ) O(n) O(n)于 O ( n 2 ) O(n^2) O(n2)之间的三种算法进行验证。
注:实现方法并不一定使该复杂度下最优算法,只是挑选了一种方法对于不同时间复杂度进行实现。
思路一: O ( k n ) O (kn) O(kn)算法
-
实现方法:
利用k轮的冒泡排序,将最大的k个数字冒泡到数组末尾。 -
伪代码:
For i = 0 to K
For j = 0 to size - 1 - i
if (data[j] > data[j + 1])
swap(data[j], data[j + 1]);
return data[data + size - K, data + size]
思路二: O ( n l o g n ) O (nlogn) O(nlogn)算法
-
实现方法:
快速排序,取数列前十位。 -
伪代码:
QUICKSORT(L, low, high)
if (low < high)
pivot = PARTITON(A, low, high)
QUICKSORT(A, low, pivot - 1)
QUICKSORT(A, pivot + 1, high)
PARTITION(L, low, high)
pivot = L.r[low];
while (low < high)
while (low < high && L.r[high] >= pivot)
high --
L.r[low] = L.r[high]
while (low < high && L.r[low] <= pivot)
low ++
L.r[high] = L.r[low]
L.r[low] = pivot
return low
思路三: O ( n l o g n ) O (nlogn) O(nlogn)算法
-
实现方法:
维护一个大小为K小顶堆,如果元素大于小顶堆堆顶元素,则替换堆顶元素并重建小顶堆。
(小顶堆:是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。) -
伪代码:
for i = k to len
// nums[i]为当前遍历数据,res[0]为小顶堆堆顶元素
if (nums[i] > res[0])
res[0] = nums[i]
adjustMinHeap(res, 0, k) //重建小顶堆
return res
- 数据测试:
使用随机数生成,均匀分布的生成了 2 ∗ 1 0 5 2*10^ 5 2∗105~ 2 ∗ 1 0 7 2*10^7 2∗107的数据集。为了减少数据的偶然性,每个数据量都进行了20次测试并取平均值。
综合分析:
综合三种方法,数据测试结果如下:

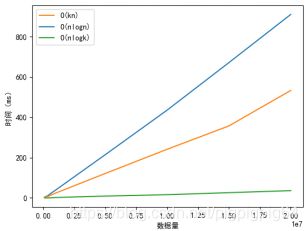
由图我们可以看出 O ( n l o g n ) > O ( k n ) > O ( n l o g k ) O(nlogn) > O(kn) > O(nlogk) O(nlogn)>O(kn)>O(nlogk)
O ( k n O(kn O(kn)与 O ( n l o g k ) O(nlogk) O(nlogk)算法都属于 O ( n ) O(n) O(n)同一级别的复杂度,显然是快于 O ( n l o g n ) O(nlogn) O(nlogn)算法的。利用小顶堆的算法设计,可以对数级地提升时间效率。
五、经验总结
在第一个问题之中对于插入排序,选择排序,冒泡排序都进行一定程度的优化,将时间效率在原有经典算法的基础上进行了提升。在查询一定资料后发现,其实可以有进一步的提升,例如将顺序查找进一步优化为二分查找操作等。但是我认为这些优化并非算法思想上的优化,不过是对于某一段函数进行优化,对于排序本质有提升,固未对于其进行测试。
对于快速排序并没有进行优化,主要原因是快速排序的优化方法目前大多是对于“基准点”选择、内部排序的优化。这些优化方法对于特定序列、相对有序序列可以有着较大程度的提升。而本次实验的数据选择为符合均匀分布的完全随机序列,这些优化并不会有较大程序的提升,固未对其进行测试。
另外,当从代码上很难得出理论分析时,可以通过设定统计量的方法进行实验(例如双向冒泡中的交换/比较次数统计)。切忌通过简单分析就得出结论,一定要有依据 的进行理论分析。