Keras深度学习实战（16）——自编码器详解

0. 前言

一张高清图像中可能包含数万个像素、文本中则可能包含成千上万个不同的单词。因此，必须将它们表示为数千维的向量，在如此高维空间中表示向量的导致我们无法高效地进行向量间的计算。
以较小的维度表示这些复杂数据有助于数据的传输、将相似的数据进行分组等。数据编码是一种无监督学习的方式，以在较低维度上表示输入，保留有关相似图像的信息，同时将信息损失降至最低，在深度学习领域，自编码器 (AutoEncoder) 便是一种流行的数据编码技术。

1. 编码的必要性

通常在输入向量维数很大的情况下使用数据编码技术。数据编码有助于将维度较大的向量转变为维数较小的向量，并且保留原始向量中绝大部分信息，而不会造成过多信息量的丢失。接下来，我们介绍对图像、文本进行编码的必要性。

1.1 对文本进行编码

为了了解文本分析中编码的必要性，我们考虑以下示例，假设我们有以下两个输入句子：

I love watching movie
I like watching movie

在传统的文本分析中，我们首先需要对两个句子中的单词进行独热编码，可以看出，两个句子中共有五个不同单词：

	I	love	watching	movie	like
I	1	0	0	0	0
like	0	1	0	0	0
watching	0	0	1	0	0
movie	0	0	0	1	0
love	0	0	0	0	1

使用单词的独热编码，可以得到两个句子的编码如下：

	I	love	watching	movie	like
I love watching movie	1	1	1	1	0
I like watching movie	1	0	1	1	1

在以上两个句子中，可以看到两个句子之间的欧几里得距离大于零，这是因为 “like” 和 “enjoy” 的编码不同。但是，从语义上讲，我们知道 “like” 和 “enjoy” 这两个词彼此非常相似。
由于两个句子中有五个不同的词，我们需要在五维空间中表示每个词。在数据编码中，我们可以以较低维度，例如，使用三维向量表示一个单词。这样，相似的单词之间的距离会更短。

1.2 对图像进行编码

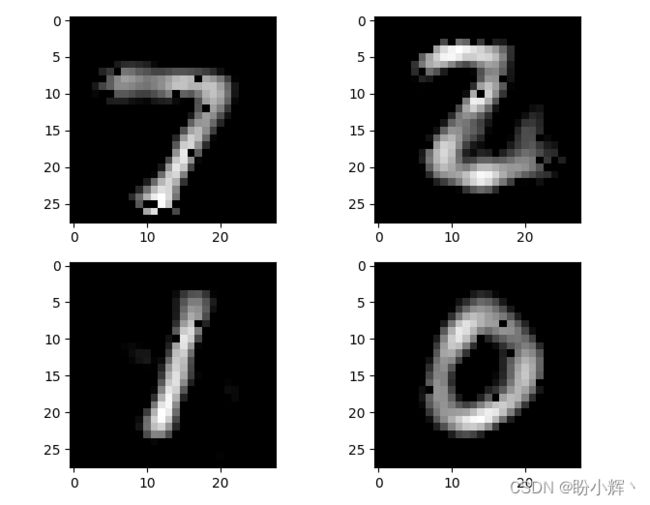
为了了解图像分析中编码的必要性，我们假设在没有图像标签的情况下按照相似度对图像进行分组，考虑 MNIST 数据集中以下具有相同标签的图像：

我们知道前面的两个图像都对应于相同的标签。但是，当我们使用欧几里得距离衡量以上两幅图像之间的距离时，该距离大于零，因为在以上两幅图像中显然包含不同的像素。
在存储图像信息时，我们也应该注意到以下问题：尽管图像共包括 28 x 28 = 784 个像素，但大多数像素列都是黑色的，因此其中并不包含有效信息，但是它们在存储信息时同样需要占据空间，造成空间浪费。
使用自编码器，我们可以以较低的维度表示以上两个图像，这样两个图像的编码之间的距离就会小得多，同时我们需要确保图像编码不会从丢失太多原始图像中的信息。

2. 使用自编码器编码图像

有多种用于图像编码的算法，其中自编码器 (AutoEncoder) 是在深度学习领域广为应用的模型，在以下各节中，我们将对比原始自编码器，多层自编码器和卷积自编码器的性能。

2.1 自编码器模型分析

自编码的目标是以更少的图像特征重建原始输入图像。自编码器将图像作为输入，并将输入图像编码为较低维度，以便我们可以仅使用输入图像的低维编码来重建原始图像。本质上，相似图像具有相似的低维编码值。
在训练编码图像模型之前，我们首先介绍自编码器的工作流程：

• 假设有一个简单数据集，该数据集中的每张图片具有 16 个像素
• 使用形状为 1 × 16 的二维数据表示图片中的 16 个像素：
  • 输入数据中的信息会在降低尺寸的同时尽可能得到保留
  • 低维空间中的向量可以称为嵌入 (embedding) / 编码向量 (encoded vector)，或瓶颈特征 (bottleneck feature) / 瓶颈向量 (bottleneck vector)，或压缩表示 (compressed representation)，或潜编码 (latent code)
• 通过将输入值与尺寸为 16 × 2 的随机权重矩阵进行矩阵乘法，可以将具有 16 个值的向量转换为 2 个值(根据矩阵乘法 $[1\times 16]\cdot [16\times 2]=[1\times 2]$)
• 低维向量表示瓶颈特征，瓶颈特征是重建原始图像所需的特征
• 使用低维瓶颈特征向量以重建输出向量：
  • 将形状为 1 × 2 二维特征向量乘以形状为 2 × 16 的矩阵，以获得形状为 1 × 16 的输出矩阵(根据矩阵乘法 $[1\times 2]\cdot [2\times 16]=[1\times 16]$)，重构与原始输入具有相同尺寸的向量
• 计算输入向量和输出向量之间的平方差之和
• 优化随机初始化的权重向量，以最小化输入和输出向量之间的平方差之和
• 所得的 2 维编码向量代表了原始输入的 16 维向量

在利用神经网络时，可以将编码向量视为连接输入和输出层的隐藏层输出。此外，训练神经网络，输入层和输出层的值完全相同，并且隐藏层的尺寸小于输入层的尺寸。
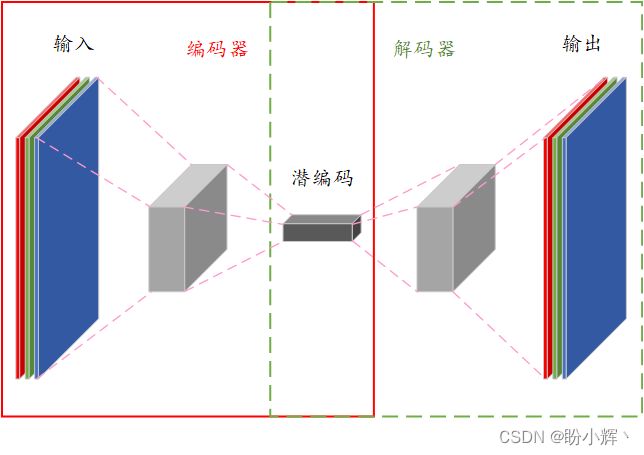
在自编码器中，用于将输入数据特征压缩为低维特征的网络称为编码器 (Encoder)，将低维特征重构为输入数据的网络称为解码器 (Decoder)。以下各节中，我们将利用 Keras 实现自编码器的多种变体。

2.2 原始自编码器

原始自编码器模型架构如下所示，在其网络中使用最少数量的隐藏层和隐藏单元重建输入：

要了解一个模型的运作过程，没有比实现这个模型更好的办法了。接下来，我们实现自编码器，使用 MNIST 数据集训练模型，以利用原始图像的低维向量重建 MNIST 图像。

(1) 导入所需库和 MNIST 数据集，并对数据集进行预处理：

import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
import matplotlib.pyplot as plt

(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], x_train.shape[1]*x_train.shape[2])
x_test = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[2])
x_train = x_train/255
x_test = x_test/255

(2) 构建自编码器网络架构，查看模型的简要架构信息：

model = Sequential()
model.add(Dense(16, input_dim=784, activation='relu'))
model.add(Dense(784, activation='relu'))
model.summary()

模型的简要架构信息输入如下，可以看到，我们正在使用 16 维的编码向量表示 784 维的图像输入：

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 16)                12560     
_________________________________________________________________
dense_1 (Dense)              (None, 784)               13328     
=================================================================
Total params: 25,888
Trainable params: 25,888
Non-trainable params: 0
_________________________________________________________________

(3) 编译并拟合模型，由于像素值是连续的，因此我们使用均方误差作为损失函数。另外，输入和输出数组是相同的——训练集中均为 x_train，验证集中均为 x_test：

model.compile(loss='mean_squared_error', optimizer='adam',metrics=['accuracy'])
model.fit(x_train, x_train,
            validation_data=(x_test, x_test),
            epochs=10,
            batch_size=512,
            verbose=1)

(4) 绘制前四个输入图像重构后得到的图像：

plt.subplot(221)
plt.imshow(model.predict(x_test[0,:].reshape(1,784)).reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(222)
plt.imshow(model.predict(x_test[1,:].reshape(1,784)).reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(223)
plt.imshow(model.predict(x_test[2,:].reshape(1,784)).reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(224)
plt.imshow(model.predict(x_test[3,:].reshape(1,784)).reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()

利用低维编码向量重构的 MNIST 数字图像如下：

(5) 为了了解自编码器的模型性能，我们将模型输出的预测结果与原始输入图像进行比较：

plt.subplot(221)
plt.imshow(x_test[0].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(222)
plt.imshow(x_test[1].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(223)
plt.imshow(x_test[2].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.subplot(224)
plt.imshow(x_test[3].reshape(28,28), cmap=plt.get_cmap('gray'))
plt.show()

原始 MNIST 数字图像如下，可以看到，与原始输入图像相比，重建的图像较为模糊：

为了解决模糊问题，我们构建深度较深的多层自编码器，其具有更多参数，从而有可能更好地使用低维编码向量表示原始图像。

2.2 多层自编码器

多层自编码器架构如下所示，模型中有更多隐藏层将输入层连接到输出层。本质上，多层自编码器在其网络中使用的更多隐藏层来重建输入：

(1) 要构建多层自编码器，加载数据与预处理步骤与原始自编码器中的步骤相同，只需要将网络体系结构修改为包括多层隐藏层的神经网络：

model = Sequential()
model.add(Dense(100, input_dim=784, activation='relu'))
model.add(Dense(16,activation='relu'))
model.add(Dense(100,activation='relu'))
model.add(Dense(784, activation='relu'))
model.summary()

模型简要架构信息输出如下：

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_2 (Dense)              (None, 100)               78500     
_________________________________________________________________
dense_3 (Dense)              (None, 16)                1616      
_________________________________________________________________
dense_4 (Dense)              (None, 100)               1700      
_________________________________________________________________
dense_5 (Dense)              (None, 784)               79184     
=================================================================
Total params: 161,000
Trainable params: 161,000
Non-trainable params: 0
_________________________________________________________________

在多层自编码器网络中，第一个隐藏层有 100 个神经元，第二个隐藏层中包含 16 个神经元，即编码向量具有 16 个维度，而第三个隐藏层与第一隐藏层一样具有 100 个神经元。

(2) 定义网络体系结构后，编译并拟合所构建自编码器：

model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, x_train,
            validation_data=(x_test, x_test),
            epochs=10,
            batch_size=512,
            verbose=1)

多层自编码器模型的重建输出如下，可以看到，与原始图像相比，重建后的图像仍然较为模糊，但相比于原始自编码器，已有相当程度的改善：

2.3 卷积自编码器

我们已经训练了原始和多层自编码器，接下来，我们将了解卷积自编码器如何利用低维向量重构原始图像。卷积自编码器模型架构如下所示：

本质上，卷积自编码器在其网络中使用卷积、池化操作来代替原始自编码器的全连接操作，并使用反卷积操作 (Conv2DTranspose) 对特征图进行上采样。
(1) 卷积自编码器的模型架构所需的输入形状与其他类型的自编码器不同，因此需要对输入图像进行整形，以便可以将其传递给 Conv2D 方法：

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.reshape(x_train.shape[0], x_train.shape[1], x_train.shape[2], 1)
x_test = x_test.reshape(x_test.shape[0], x_test.shape[1], x_test.shape[2], 1)
x_train = x_train/255
x_test = x_test/255

(2) 接下来，我们实现卷积自动编码器的模型体系结构：

from keras.layers import Conv2D, MaxPooling2D, Flatten, Reshape, Conv2DTranspose

model = Sequential()
model.add(Conv2D(32, (3,3), input_shape=(28, 28,1), activation='relu',padding='same',name='conv1'))
model.add(MaxPooling2D(pool_size=(2, 2),name='pool1'))
model.add(Conv2D(64, (3,3), activation='relu',padding='same',name='conv2'))
model.add(MaxPooling2D(pool_size=(2, 2),name='pool2'))
model.add(Conv2D(64, (3,3), activation='relu',padding='same',name='conv3'))
model.add(MaxPooling2D(pool_size=(2, 2),name='pool3'))
model.add(Conv2D(16, (3,3), activation='relu',padding='same',name='conv4'))
model.add(MaxPooling2D(pool_size=(2, 2),name='pool4'))
model.add(Flatten(name='flatten'))
model.add(Reshape((1,1,16)))
model.add(Conv2DTranspose(16, kernel_size = (3,3), activation='relu'))
model.add(Conv2DTranspose(64, kernel_size = (5,5), activation='relu'))
model.add(Conv2DTranspose(64, kernel_size = (8,8), activation='relu'))
model.add(Conv2DTranspose(32, kernel_size = (15,15), activation='relu'))
model.add(Conv2D(1, (3, 3), activation='relu',padding='same'))
model.summary()

在以上代码中，我们定义了一个卷积自编码器，首先提取输入图像特征以降维图像特征，获取 16 维的特征编码向量，最后对其进行上采样，以便可以重构输入图像。该模型的简要信息输出如下：

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv1 (Conv2D)               (None, 28, 28, 32)        320       
_________________________________________________________________
pool1 (MaxPooling2D)         (None, 14, 14, 32)        0         
_________________________________________________________________
conv2 (Conv2D)               (None, 14, 14, 64)        18496     
_________________________________________________________________
pool2 (MaxPooling2D)         (None, 7, 7, 64)          0         
_________________________________________________________________
conv3 (Conv2D)               (None, 7, 7, 64)          36928     
_________________________________________________________________
pool3 (MaxPooling2D)         (None, 3, 3, 64)          0         
_________________________________________________________________
conv4 (Conv2D)               (None, 3, 3, 16)          9232      
_________________________________________________________________
pool4 (MaxPooling2D)         (None, 1, 1, 16)          0         
_________________________________________________________________
flatten (Flatten)            (None, 16)                0         
_________________________________________________________________
reshape (Reshape)            (None, 1, 1, 16)          0         
_________________________________________________________________
conv2d_transpose (Conv2DTran (None, 3, 3, 16)          2320      
_________________________________________________________________
conv2d_transpose_1 (Conv2DTr (None, 7, 7, 64)          25664     
_________________________________________________________________
conv2d_transpose_2 (Conv2DTr (None, 14, 14, 64)        262208    
_________________________________________________________________
conv2d_transpose_3 (Conv2DTr (None, 28, 28, 32)        460832    
_________________________________________________________________
conv2d (Conv2D)              (None, 28, 28, 1)         289       
=================================================================
Total params: 816,289
Trainable params: 816,289
Non-trainable params: 0
_________________________________________________________________

(3) 最后，编译并拟合模型

from keras.optimizers import Adam
adam = Adam(lr=0.001)
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, x_train,
            validation_data=(x_test, x_test),
            epochs=10,
            batch_size=512,
            verbose=1)

模型训练完成后，使用模型对前四个测试数据样本进行预测，绘制重构的图像如下所示：

可以看到，使用卷积自编码器得到的图像重构效果比使用原始 (Vanilla) 和多层自编码器的效果更好。

3. 自编码器应用

在编码的必要性部分中，我们假设相似的图像将具有相似的嵌入，而不相似图像的嵌入间的距离较大。但是，我们并没有对嵌入进行详细的相似性度量。

3.1 低维潜编码的相似性度量

在本节中，我们将在 2D 空间中绘制嵌入，使用 t-SNE 技术将利用自编码器得到的 16 维潜编码向量压缩到二维空间。由于相似的图像应在二维平面中聚类在一起，我们可以验证相似的图像是否具有相似的嵌入。接下来，我们在二维平面中表示所有测试图像的嵌入。

3.2 潜编码可视化

(1) 使用卷积自编码器提取测试数据集中所有图像( 10000 张)的 16 维特征向量：

from keras.models import Model
layer_name = 'flatten'
intermediate_layer_model = Model(inputs=model.input,outputs=model.get_layer(layer_name).output)
intermediate_output = intermediate_layer_model.predict(x_test)

(2) 使用 t-SNE 生成二维向量：

from sklearn.manifold import TSNE
import pandas as pd
tsne_model = TSNE(n_components=2, verbose=1, random_state=0)
tsne_img_label = tsne_model.fit_transform(intermediate_output)
tsne_df = pd.DataFrame(tsne_img_label, columns=['x', 'y'])
tsne_df['image_label'] = y_test

(3) 绘制使用 t-SNE 技术得到测试图像的二维嵌入的可视化图像：

from matplotlib.colors import ListedColormap

colors = ListedColormap(['#EE7C6B', '#EC870E', '#C7C300', '#489620', '#008C5E', '#00B2BF', '#184785', '#3A2885', '#52096C', '#A2007C'])
values = [label for label in tsne_df['image_label']]
classes = []
for label in tsne_df['image_label']:
    if label not in classes:
        classes.append(label)
scatter=plt.scatter(tsne_df['x'], tsne_df['y'], c=values, cmap=colors)
plt.legend(handles=scatter.legend_elements()[0], labels=classes)
plt.show()

二维空间中嵌入的可视化如下：

从上图中，我们可以看到，具有相同标签的图像在二维空间形成了簇，也就是说，它们的 2 维编码向量是相似的。

小结

对于高维输入向量的压缩对于许多应用来说都是至关重要的，不仅可以降低数据处理难度，同时也可以增加数据传输效率。本文介绍了在深度学习领域常用的数据编码技术——自编码器，并使用 MNIST 数据集训练了多个自编码器变体模型；最后，还将二维编码向量进行可视化，以验证相似的图像将具有相似的嵌入。

系列链接

Keras深度学习实战（1）——神经网络基础与模型训练过程详解
Keras深度学习实战（2）——使用Keras构建神经网络
Keras深度学习实战（3）——神经网络性能优化技术
Keras深度学习实战（4）——深度学习中常用激活函数和损失函数详解
Keras深度学习实战（5）——批归一化详解
Keras深度学习实战（6）——深度学习过拟合问题及解决方法
Keras深度学习实战（7）——卷积神经网络详解与实现
Keras深度学习实战（8）——使用数据增强提高神经网络性能
Keras深度学习实战（9）——卷积神经网络的局限性
Keras深度学习实战（10）——迁移学习详解
Keras深度学习实战（11）——可视化神经网络中间层输出
Keras深度学习实战（12）——面部特征点检测
Keras深度学习实战（13）——目标检测基础详解
Keras深度学习实战（14）——从零开始实现R-CNN目标检测
Keras深度学习实战（15）——从零开始实现YOLO目标检测