rbf核函数_高斯过程回归础（使用GPy和模拟函数数据集）

为什么要了解高斯过程呢？因为不了解高斯过程就不能聊贝叶斯优化。

假设有这么一个函数：

。现在有训练的数据y和一堆X。然后来了一个新的X让你用既有的数据去预测者个新的X所对应的y。

高斯过程（回归）的思路是：因为y之间的关系是由X之间的关系决定的。所以可以利用新来的X和既有的X之间的关系来对新来的X的y进行推测。在这里有用到联合概率分布，也就是给定一对X和y同时出现时的概率分布，比如说丢骰子，掷出六的同时是我丢骰子的概率。之后还有b。b从概率分布里取一个值的时候，我们就可以得到一个确定的y。

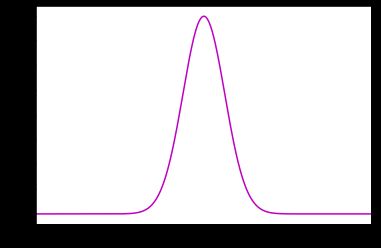
所以我们可以对原本的b进行假设。假设它是服从一个平均值为0，方差是

的高斯分布。这里涉及一个很抽象的词叫“抽样”。

首先，因为b的取值是服从一个平均值为0，方差是

的高斯分布，所以它的概率分布图长成这样的，这里我让它的方差是1:

import numpy as np
import matplotlib.pyplot as plt
 
from scipy.stats import norm
import matplotlib.pyplot as plt
 
x = np.arange(-8,8,0.01)
y = norm.pdf(x,0,1)
 
plt.plot(x,y,color='m')
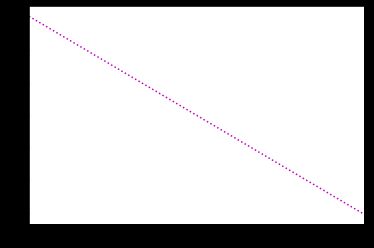
plt.xlim(-8,8)

纵轴是概率，横轴是取值。因为平均值是0所以峰值在0

但是b其实不是一个值而是一堆服从高斯分布的值。所以比如x的取值是-1，-0.9...0, 0.1...0.9, 1的话，对于高斯分布里的每一个b都会有一个y。比如说从高斯分布里面取两个b1=0.1，b2=-0.38，然后作图之后就得到了两个抽样出来的样本:

b1 = 0.1*x
plt.plot(x,b1,color='m',linestyle = "dotted")
plt.xlim(-8,8)

另一个:

b2 = -0.38*x
plt.plot(x,b2,color='m',linestyle = "dotted")
plt.xlim(-8,8)

这是两个抽样。那如果把高斯分布里面所有值全部抽样之后会是什么样子呢？

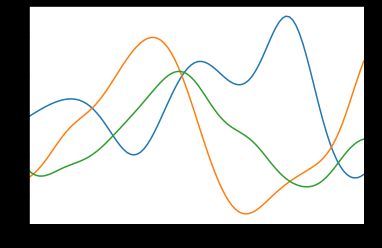
首先，这里点跟点之间的关系是线性关系，所以给它取个名字叫'linear'。这里我们使用一个包叫GPy，安装方法就是pip install GPy。由于我们将点和点之间的关系假设为线性关系，这里我们把kernel设定为linear。我理解的kernel就是种针对训练数据集x里面点和点之间关系所进行的特殊计算。

比如说抽样10次，大概就是这样:

import GPy

np.random.seed(seed=9527)
N = 100
x = np.linspace(-1, 1, N)
x = x[:, None]

kernel = GPy.kern.Linear(input_dim=1)
cov = kernel.K(x, x)
mu = np.zeros(N)
y = np.random.multivariate_normal(mu, cov, size=20)

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
for i in range(10):
    ax.plot(x[:], y[i,:])
plt.xlim(-1,1)

然后你可以从里面找一个最接近真正数据的线。这样做的好处是我们可以直观的看到y的不确定性，也就是y的变动是在一个范围里面的。

如果训练集的各个样本之间的关系仅仅是线性的话那也未必太僵化了。于是为了能使的模型能考虑更复杂的高维非线性的关系，一般用的比较多的是高斯核函数，也就是假设训练集里面每一个数据都服从高斯分布。数据之间的关系可以用以下表示:

当这里的高斯分布的γ等于1的时候，利用这个kernerl同样的可以对数据进行抽样。输入的是某一个X，然后计算完它和所有的数据之间的关系或者说距离之后求和作为新输出的y的方差。然后利用平均值为0这个性质就可以对y进行抽样了。这里和线性kernel是一样的也可以通过抽样得到y的不确定性。

import GPy
import numpy as np
import matplotlib.pyplot as plt

kernel1 = GPy.kern.RBF(input_dim=1, variance=1)
#调出RBF也就是高斯kernel， 设定输入次元1，方差1
np.random.seed(seed=123)
#同样准备100个点
N = 100
x = np.linspace(-1, 1, N)
x = x[:, None]
mu = np.zeros(N)
cov = kernel.K(x, x)
#20次抽样
y_sim = np.random.multivariate_normal(mu, cov, size=20)

抽样了20次。下面是抽样3次的结果:

通过这样的方式，高斯过程不仅可以输出一个预测值，还可以对目标值的不确定性进行把握。接下来就试一试高斯过程回归。

为了更好的看效果，这里就用一个比较简单的非线性函数做一个数据集。然后从里面抽一部分数据出来作为训练集。

n=50
x= np.linspace(1, 23*np.pi, n)
y= 3.22*np.sin(0.2*x)+2.33*np.cos(0.03*x)
missing_rate = 0.15
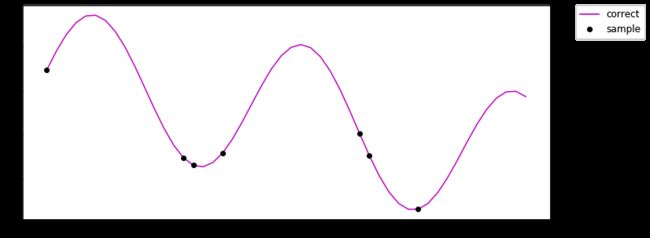
index = np.sort(np.random.choice(np.arange(n), int(n*missing_rate), replace=False))

画图出来长成这样:

from matplotlib import pyplot as plt
%matplotlib inline

plt.figure(figsize=(12, 5))

plt.plot(x, y, color='m', label='correct')


plt.plot(x[index], y[index], 'o', color='black', label='sample')

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
plt.show()

这里的黑点就是抽出来的作为训练集的样本。然后训练这些黑点来预测整个函数。

x_train = np.copy(x[index])
y_train = np.copy(y[index])
x_test = np.copy(x)

设定kernel

kernel = GPy.kern.RBF(input_dim=1, variance=1)

输入次元为1，方差随便选了1。这里有点类似sklearn。

model = GPy.models.GPRegression(x_train[:, None], y_train[:, None], kernel=kernel)
model.optimize()
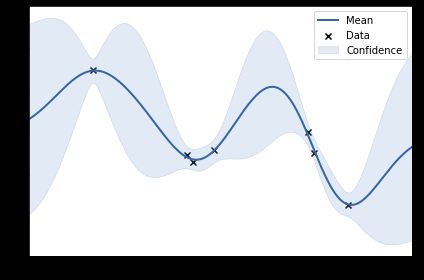
model.plot()

它自带了一个作图功能，这里可以看到图像里面的蓝色的面积就代表模型的不确定性，显然数据密度高的地方不确定性就越低。这里的预测结果是这样的:

y_qua_pred = model.predict_quantiles(x_test[:, None], quantiles=(2.5, 50, 97.5))[0]
y_qua_cov= model.predict_quantiles(x_test[:, None], quantiles=(2.5, 50, 97.5))[1]

一个是预测值一个是方差。

反正跟sklearn的一般模型一样可以输出的不仅是模型的预测值还可以输出模型的不确定性，利用这两个东西可以去算哪些实验参数的候补是更需要做的。