本文介绍了CCA解决的问题,CCA原理的推导过程,以及对计算结果物理意义的解释。并且通过SPSS和R操作演示了一个关于CCA的例子。数据文件下载参考[8],SPSS输出结果文件下载参考[9],R代码文件下载参考[10]。
一.CCA工作原理
1.CCA定义
首先需要搞清楚典型相关分析(Canonical Correlation Analysis)解决了什么问题,它解决的是一组变量与另外一组变量的相关问题。举个例子,比如想要量化家庭特征与家庭消费之间的关系,其中,家庭特征包括户主的年龄、家庭的年收入和户主受教育程序,而家庭消费包括每年去餐厅就餐的频率、每年外出看电影频率。
其实,这个是泛化后的问题,先来看一个更加具体的问题,不是一组变量与另外一组变量的相关问题,而是一个变量与另外一个变量的相关问题,比如计算两个变量${X}$和${Y}$的相关问题,是如何计算的呢,下面的方程是不是很眼熟:
$$ {\rho _{XY}} = \frac{{{\mathop{\rm cov}} \left( {X,Y} \right)}}{{\sqrt {{\mathop{\rm var}} \left( X \right){\mathop{\rm var}} \left( Y \right)} }} $$
再进一步的想一下,如果是计算一个变量和一组变量的相关问题呢。当然更深一步的想象就是这篇文章要讲的一组变量与另外一组变量的相关问题。先来形式化的定义CCA:假设有一组变量${X_1}, \cdots ,{X_p}$与另一组变量${Y_1}, \cdots ,{Y_q}$,要研究这两组变量的相关关系,如何给两组变量之间的相关性以数量的描述,就是CCA。
二.CCA方程推导过程
1.CCA的数学描述
假设${x_1}$表示每年去餐馆就餐的频率,${x_2}$表示每年外出看电影频率,${y_1}$表示户主的年龄,${y_2}$表示家庭的年收入,${y_3}$表示户主受教育程度。典型相关分析的思想是找出第一对线性组合,使其具有最大相关性:
$$ \begin{array}{l} {u_1} = {a_{11}}{x_1} + {a_{21}}{x_2}+...+ {a_{p1}}{x_p}\\ {v_1} = {b_{11}}{y_1} + {b_{21}}{y_2} + {b_{31}}{y_3} +...+{b_{q1}}{y_q}\\ \rho \left( {{u_1},{v_1}} \right) = ? \\ \end{array} $$
然后再找第二对线性组合,使其具有次大相关性:
$$ \begin{array}{l} {u_2} = {a_{12}}{x_1} + {a_{22}}{x_2}+...+ {a_{p2}}{x_p} \\ {v_2} = {b_{12}}{y_1} + {b_{22}}{y_2} + {b_{32}}{y_3} +...+{b_{q2}}{y_q} \\ \rho \left( {{u_2},{v_2}} \right) = ? \\ \end{array} $$
就这样一直进行计算下去,直到第$r$步,这两组变量的相关性被提取完毕为止,其中$r \le \min \left( {{\rm{p}},{\rm{q}}} \right)$,即可以得到$r$组变量。
2.CCA的推导过程
假设两组变量的向量${\bf{Z}} = \left( {{x_1},{x_2},...,{x_p},{y_1},{y_2},...,{y_q}} \right)$,其协方差矩阵如下:
$$ \sum = \left[ \begin{array}{l} \sum\nolimits_{11} \sum\nolimits_{12} \\ \sum\nolimits_{21} \sum\nolimits_{12} \\ \end{array} \right] $$
其中,$\sum\nolimits_{11}$是第一组变量的协方差矩阵,$\sum\nolimits_{22}$是第二组变量的协方差矩阵,$\sum\nolimits_{12}$和$\sum\nolimits_{21}$是$X$和$Y$的协方差矩阵,它们之间的关系是转置相等,即$\sum\nolimits_{12} = {\sum\nolimits_{21} ^{\rm{T}}}$。这样两组变量的第一对线性组合记为:
$$ \begin{array}{l} {{\bf{u}}_1} = {\bf{a}}_1^{\rm{T}}{\bf{X}} \\ {{\bf{v}}_1} = {\bf{b}}_1^{\rm{T}}{\bf{Y}} \\ \end{array} $$
其中${\bf{a}}_1$和${\bf{b}}_1$表示:
$$ \begin{array}{l} {{\bf{a}}_1} = {\left( {{a_{11}},{a_{21}},...,{a_{p1}}} \right)^{\rm{T}}} \\ {{\bf{b}}_1} = {\left( {{b_{11}},{b_{21}},...,{b_{q1}}} \right)^{\rm{T}}} \\ \end{array} $$
接下来推导${\rho _{{{\bf{u}}_1},{{\bf{v}}_1}}}$的计算,通过求${\bf{a}}_1$和${\bf{b}}_1$,使${\rho _{{{\bf{u}}_1},{{\bf{v}}_1}}}$最大,这个是CCA最核心的思想:
$$ \begin{array}{l} {\mathop{\rm var}} \left( {{{\bf{u}}_1}} \right) = {\bf{a}}_1^{\rm{T}}{\mathop{\rm var}} \left( {\bf{X}} \right){{\bf{a}}_1} = {\bf{a}}_1^{\rm{T}}\sum\nolimits_{11} {} {{\bf{a}}_1} = 1 \\ {\mathop{\rm var}} \left( {{{\bf{v}}_1}} \right) = {\bf{b}}_1^T{\mathop{\rm var}} \left( {\bf{Y}} \right){{\bf{b}}_1} = {\bf{b}}_1^T\sum\nolimits_{22} {} {{\bf{b}}_1} = 1 \\ {\rho _{{{\bf{u}}_1},{{\bf{v}}_1}}} = {\rm{cov}}\left( {{{\bf{u}}_1},{{\bf{v}}_1}} \right) = {\bf{a}}_1^{\rm{T}}{\rm{cov}}\left( {{\bf{X}},{\bf{Y}}} \right){{\bf{b}}_1} = {\bf{a}}_1^{\rm{T}}\sum\nolimits_{12} {} {{\bf{b}}_1} \\ \end{array} $$
接下来就是典型相关系数的过程。根据高等数学中条件极致的求法,即拉格朗日乘数法,通过引入拉格朗日乘数$\lambda$和$\nu$来求极值的问题,转换为求方程1的极大值:
$$ \phi \left( {{{\bf{a}}_1},{{\bf{b}}_1}} \right) = {\bf{a}}_1^{\rm{T}}\sum\nolimits_{12} {} {{\bf{b}}_1} - \frac{\lambda }{2}\left( {{\bf{a}}_1^{\rm{T}}\sum\nolimits_{11} {{{\bf{a}}_1}} - 1} \right) - \frac{\nu }{2}\left( {{\bf{b}}_1^{\rm{T}}\sum\nolimits_{22} {{{\bf{b}}_1}} - 1} \right) $$
接下来就是求极大值的思路了,各种求偏导,方程2如下所示:
$$ \begin{array}{l} \frac{{\partial \phi }}{{\partial {{\bf{a}}_1}}} = \sum\nolimits_{12} {{{\bf{b}}_1}} - \lambda \sum\nolimits_{11} {{{\bf{a}}_1}} = 0 \\ \frac{{\partial \phi }}{{\partial {{\bf{b}}_1}}} = \sum\nolimits_{21} {{{\bf{a}}_1}} - v\sum\nolimits_{22} {{{\bf{b}}_1}} = 0 \\ \end{array} $$
方程3如下所示:
$$ \begin{array}{l} \sum\nolimits_{12} {{{\bf{b}}_1}} - \lambda \sum\nolimits_{11} {{{\bf{a}}_1}} = 0 \\ \sum\nolimits_{21} {{{\bf{a}}_1}} - v\sum\nolimits_{22} {{{\bf{b}}_1}} = 0 \\ \end{array} $$
将方程3分别左乘${\bf{a}}_1^{\rm{T}}$和${\bf{b}}_1^{\rm{T}}$,得到方程4:
$$ \begin{array}{l} {\bf{a}}_1^{\rm{T}}\sum\nolimits_{12} {{{\bf{b}}_1}} - \lambda {\bf{a}}_1^{\rm{T}}\sum\nolimits_{11} {{{\bf{a}}_1}} = 0 \\ {\bf{b}}_1^{\rm{T}}\sum\nolimits_{21} {{{\bf{a}}_1}} - v{\bf{b}}_1^{\rm{T}}\sum\nolimits_{22} {{{\bf{b}}_1}} = 0 \\ \end{array} $$
进一步推导得出方程5:
$$ \begin{array}{l} {\bf{a}}_1^{\rm{T}}\sum\nolimits_{12} {{{\bf{b}}_1}} = \lambda \\ {\bf{b}}_1^{\rm{T}}\sum\nolimits_{21} {{{\bf{a}}_1}} = v \\ \end{array} $$
因此得到方程6:
$$ \lambda = v = {\bf{a}}_1^{\rm{T}}\sum\nolimits_{12} {{{\bf{b}}_1}} = {\rho _{\left( {{{\bf{u}}_1},{\bf{v}}1} \right)}} $$
可见$\lambda$和$v$是相等的,并且就是要求的${\rho _{{{\bf{u}}_1},{{\bf{v}}_1}}}$。
将$\sum\nolimits_{12} \sum\nolimits_{22}^{ - 1}$左乘方程3的第二式,得到方程7:
$$ \sum\nolimits_{12} \sum\nolimits_{22}^{ - 1} \sum\nolimits_{21} {{\bf{a}}_1} - v\sum\nolimits_{12} \sum\nolimits_{22}^{ - 1} \sum\nolimits_{22} {} {{\bf{b}}_1} = 0 $$
进一步简化得到方程8:
$$ \sum\nolimits_{12} \sum\nolimits_{22}^{ - 1} \sum\nolimits_{21} {} {{\bf{a}}_1} - v\sum\nolimits_{12} {{\bf{b}}_1} = 0 $$
将方程3的第一式代入方程8,得到方程9:
$$ \sum\nolimits_{12} \sum\nolimits_{22}^{ - 1} \sum\nolimits_{21} {{\bf{a}}_1} - {\lambda ^2}\sum\nolimits_{11} {{\bf{a}}_1} = 0 $$
将方程9左乘$\sum\nolimits_{11}^{ - 1}$得到方程10:
$$ \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{12} {} \sum\nolimits_{22}^{ - 1} {} \sum\nolimits_{21} {} {{\bf{a}}_1} - {\lambda ^2}{{\bf{a}}_1} = 0 $$
在方程10中,$\sum\nolimits_{11}^{ - 1} \sum\nolimits_{12} \sum\nolimits_{22}^{ - 1} \sum\nolimits_{21}$的特征根是${\lambda ^2}$,相应的特征向量为${{\bf{a}}_1}$。
将$\sum\nolimits_{12} \sum\nolimits_{11}^{ - 1}$左乘方程3的第一式,并且将第二式代入得到方程11:
$$ \begin{array}{l} \sum\nolimits_{21} {} \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{21} {{{\bf{b}}_1}} - \lambda \sum\nolimits_{12} {{{\bf{a}}_1}} = 0 \\ \sum\nolimits_{21} {} \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{12} {{{\bf{b}}_1}} - {\lambda ^2}\sum\nolimits_{22} {{{\bf{b}}_1}} = 0 \\ \sum\nolimits_{22}^{ - 1} {} \sum\nolimits_{21} {} \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{12} {{{\bf{b}}_1}} - {\lambda ^2}{{\bf{b}}_1} = 0 \\ \end{array} $$
在方程11中,$\sum\nolimits_{22}^{ - 1} \sum\nolimits_{21} \sum\nolimits_{11}^{ - 1} \sum\nolimits_{12}$的特征根是${\lambda ^2}$,相应的特征向量为${{\bf{b}}_1}$。
令${{\bf{M}}_{\rm{1}}} = \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{12} {} \sum\nolimits_{22}^{ - 1} {} \sum\nolimits_{21} {}$和${{\bf{M}}_2}{\rm{ = }}\sum\nolimits_{22}^{ - 1} {} \sum\nolimits_{21} {} \sum\nolimits_{11}^{ - 1} {} \sum\nolimits_{12} {}$,得到方程12:
$$ \begin{array}{l} {{\bf{M}}_{\rm{1}}}{{\bf{a}}}{\rm{ = }}{\lambda ^2}{{\bf{a}}} \\ {{\bf{M}}_2}{{\bf{b}}}{\rm{ = }}{\lambda ^2}{{\bf{b}}} \\ \end{array} $$
至此可以得出结论:第一个典型相关系数为$\lambda_1$(最大特征值),其中$\lambda _1^2$既是${\bf{M}}_{\rm{1}}$又是${\bf{M}}_{\rm{2}}$的特征根,第一对典型变量的系数${{\bf{a}}_1}$和${{\bf{b}}_1}$是相应于${\bf{M}}_{\rm{1}}$和${\bf{M}}_{\rm{2}}$的特征向量。这样就把典型相关分析的求解转换成了求${\bf{M}}_{\rm{1}}$和${\bf{M}}_{\rm{2}}$的特征根和特征向量的问题。
说明:第一对典型变量提取了原始变量$X$和$Y$之间相关的主要部分,如果这部分不能足以解释原始变量,可以在剩余的相关中再求出第二对典型变量和它们的典型相关系数。如此反复,直到这两组变量的相关性被提取完毕为止。
3.CCA的物理意义
还是以量化家庭特征与家庭消费之间的关系为例子,假设${x_1}$表示每年去餐馆就餐的频率,${x_2}$表示每年外出看电影频率,${y_1}$表示户主的年龄,${y_2}$表示家庭的年收入,${y_3}$表示户主受教育程度。如果计算出第一典型相关系数为0.687948,第二典型相关系数为0.186865。第一典型变量和第二典型变量代入方程如下所示:
(1)第一对典型变量
$$ \begin{array}{l} {u_1} = {0.9866}{x_1} + {0.8872}{x_2} \\ {v_1} = {0.4211}{y_1} + {0.9822}{y_2} + {0.5145}{y_3} \\ \end{array} $$
- ${u_1}$量化的是家庭消费特征,它与${x_1}$和${x_2}$的相关系数分别为0.9866和0.8872,这2个值都是比较高的。
- ${v_1}$量化的是家庭特征,它与${y_2}$的相关系数为0.9822,其它的相关系数较小,因此${v_1}$主要代表的就是家庭收入。
- ${u_1}$和${v_1}$的相关系数为0.687948,说明一个家庭的消费和家庭的收入关系密切。
(2)第二对典型变量
$$ \begin{array}{l} {u_2} = {-0.1632}{x_1} + {0.4614}{x_2} \\ {v_2} = {0.8464}{y_1} + {-0.1101}{y_2} + {0.3013}{y_3} \\ \end{array} $$
- ${u_2}$和${x_2}$的相关系数为0.4614,可见${u_2}$主要代表的是每年外出看电影频率。
- ${v_2}$和${y_1}$的相关系数为0.8464,可见${v_2}$主要代表的是家庭成员的年龄特征。
- ${u_2}$和${v_2}$的相关系数为0.186865,说明一个家庭每年外出看电影频率和家庭成员的年龄特征关系密切。
三.CCA代码例子
1.SPSS28实现
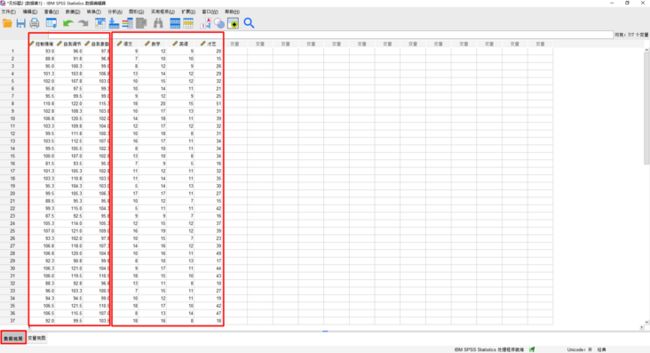
(1)变量视图和数据视图 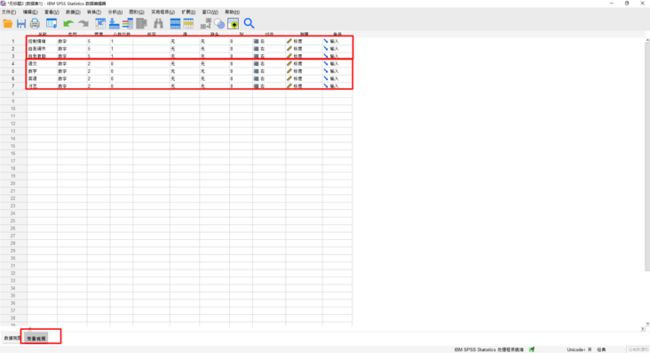
(2)分析->相关->典型相关分析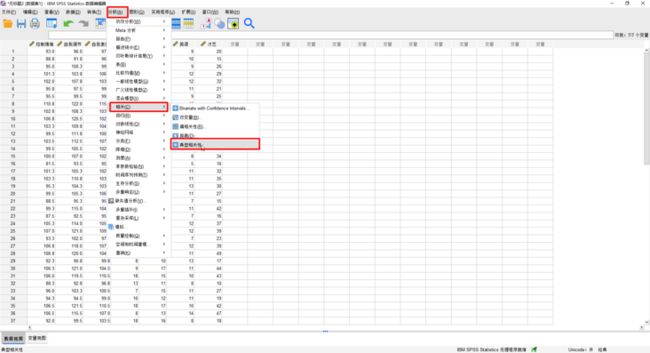
将控制情绪、自我调节、自我激励作为集合1,将语文、数学、英语和才艺作为集合2: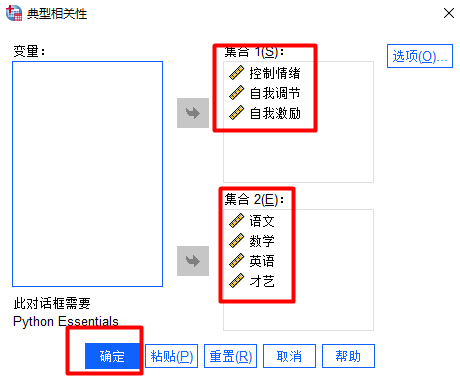
(3)生成结果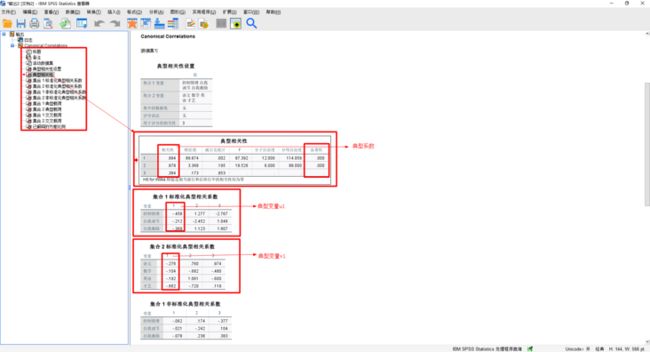
2.R编程实现
(1)安装R包
操作系统使用的Windows10,版本号为20H2,R语言版本使用64位的R-3.6.3。期初在安装R包的时候总是报错,经过查找资料,需要将Packages页面中的第2和3个复选框去掉,重启RStudio即可: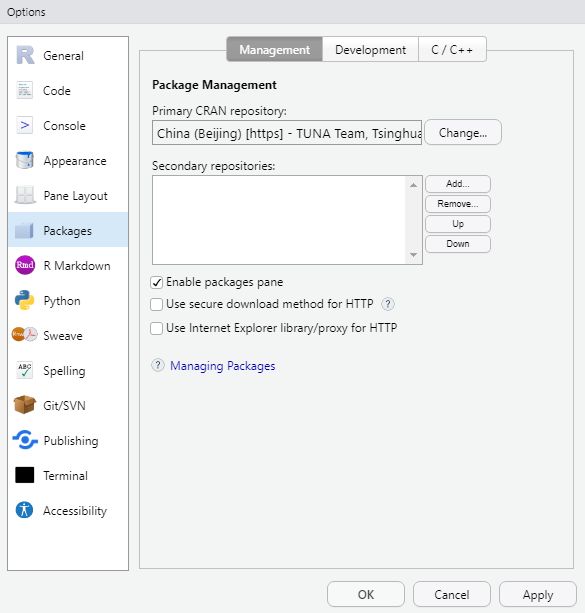
依次安装openxlsx、CCA和CCP包:
install.packages("openxlsx", dependencies=TRUE)
install.packages("CCA", dependencies=TRUE)
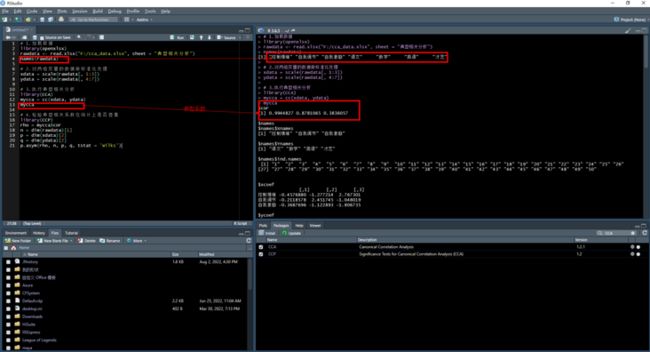
install.packages("CCP", dependencies=TRUE)# 1.加载数据
library(openxlsx)
rawdata <- read.xlsx("F:/cca_data.xlsx", sheet = "典型相关分析")
names(rawdata)
# 2.对两组变量的数据做标准化处理
xdata = scale(rawdata[, 1:3])
ydata = scale(rawdata[, 4:7])
# 3.执行典型相关分析
library(CCA)
mycca = cc(xdata, ydata)
mycca
# 4.检验典型相关系数在统计上是否显著
library(CCP)
rho = mycca$cor
n = dim(rawdata)[1]
p = dim(xdata)[2]
q = dim(ydata)[2]
p.asym(rho, n, p, q, tstat = 'Wilks')(3)输出结果
> # 1.加载数据
> library(openxlsx)
> rawdata <- read.xlsx("F:/cca_data.xlsx", sheet = "典型相关分析")
> names(rawdata)
[1] "控制情绪" "自我调节" "自我激励" "语文" "数学" "英语" "才艺"
>
> # 2.对两组变量的数据做标准化处理
> xdata = scale(rawdata[, 1:3])
> ydata = scale(rawdata[, 4:7])
>
> # 3.执行典型相关分析
> library(CCA)
> mycca = cc(xdata, ydata)
> mycca
$cor
[1] 0.9944827 0.8781065 0.3836057
$names
$names$Xnames
[1] "控制情绪" "自我调节" "自我激励"
$names$Ynames
[1] "语文" "数学" "英语" "才艺"
$names$ind.names
[1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14" "15" "16" "17" "18" "19" "20" "21" "22" "23" "24" "25" "26"
[27] "27" "28" "29" "30" "31" "32" "33" "34" "35" "36" "37" "38" "39" "40" "41" "42" "43" "44" "45" "46" "47" "48" "49" "50"
$xcoef
[,1] [,2] [,3]
控制情绪 -0.4576880 -1.277214 2.767301
自我调节 -0.2118578 2.451745 -1.048019
自我激励 -0.3687696 -1.122893 -1.806735
$ycoef
[,1] [,2] [,3]
语文 -0.2755155 -0.7599743 -0.9739351
数学 -0.1040424 0.6822849 0.4802843
英语 -0.1916330 -1.0607433 0.5995720
才艺 -0.6620838 0.7198947 -0.1194195
$scores
$scores$xscores
[,1] [,2] [,3]
1 0.97838292 -0.362539552 0.81938141
2 1.40651588 -0.410239408 0.05351720
......
49 -0.68982939 -1.133476875 0.34804581
50 -0.86681530 1.107521445 0.63269334
$scores$yscores
[,1] [,2] [,3]
1 0.97479103 0.09430244 -0.08851950
2 1.40034960 -0.76140727 0.45769014
......
49 -0.64792179 -1.26188686 -0.66195176
50 -0.73030445 0.62990478 0.08452069
$scores$corr.X.xscores
[,1] [,2] [,3]
控制情绪 -0.9798776 0.0006477883 0.199598477
自我调节 -0.9464085 0.3228847489 -0.007504408
自我激励 -0.9518620 -0.1863009724 -0.243414776
$scores$corr.Y.xscores
[,1] [,2] [,3]
语文 -0.6348095 -0.1894059 -0.24988439
数学 -0.7171837 0.2086069 0.02598458
英语 -0.6436782 -0.4402237 0.22027544
才艺 -0.9388771 0.1734549 0.03614570
$scores$corr.X.yscores
[,1] [,2] [,3]
控制情绪 -0.9744713 0.0005688272 0.076567107
自我调节 -0.9411869 0.2835272081 -0.002878734
自我激励 -0.9466102 -0.1635921013 -0.093375287
$scores$corr.Y.yscores
[,1] [,2] [,3]
语文 -0.6383313 -0.2156981 -0.65140953
数学 -0.7211626 0.2375644 0.06773775
英语 -0.6472493 -0.5013329 0.57422365
才艺 -0.9440859 0.1975329 0.09422619
> # 4.检验典型相关系数在统计上是否显著
> library(CCP)
> rho = mycca$cor
> n = dim(rawdata)[1]
> p = dim(xdata)[2]
> q = dim(ydata)[2]
> p.asym(rho, n, p, q, tstat = 'Wilks')
Wilks' Lambda, using F-approximation (Rao's F):
stat approx df1 df2 p.value
1 to 3: 0.002148472 87.391525 12 114.0588 0.000000e+00
2 to 3: 0.195241267 18.526265 6 88.0000 8.248957e-14
3 to 3: 0.852846693 3.882233 2 45.0000 2.783536e-02从结果上来看,无论是SPSS还是R,计算的结果都是完全相同的。
参考文献:
[1]典型相关分析:https://www.bilibili.com/vide...
[2]sklearn.cross_decomposition.CCA:https://scikit-learn.org/stab...
[3]协方差矩阵:https://baike.baidu.com/item/协方差矩阵/9822183
[4]典型相关分析(CCA)原理及Python实现:https://developer.aliyun.com/...
[5]CCA典型关联分析原理与Python案例:https://cloud.tencent.com/dev...
[6]典型关联分析(CCA)原理总结:https://www.cnblogs.com/pinar...
[7]典型相关分析:https://www.docin.com/p-21267...
[8]数据文件cca_data.xlsx:https://url39.ctfile.com/f/25... (访问密码: 2096)
[9]SPSS输出结果文件:https://url39.ctfile.com/f/25... (访问密码: 2096)
[10]R代码文件:https://url39.ctfile.com/f/25... (访问密码: 2096)
本文由mdnice多平台发布