智能算法集成测试平台V0.1实战开发
文章目录
- 前言
- 版权
- 2022.7.4
- 集成算法
-
- 项目结构
- 基本粒子群算法SPSO
-
- 数据结构
- 相关配置
- 实现代码
- 目标函数
- 参数优化(单种群)PSO系列算法
-
- LPSO
- DPSO
- NPSO
- 自适应PSO(VCAPSO)
-
- 参数配置
- 核心代码
- 综合粒子群算法(CLPSO)
- 多种群算法
-
- MPSO 算法
- HPSO算法
- 后续工作
前言
兜兜转转了一圈,想要和其他的粒子群算法做个对比测试,结果发现,那帮西崽木得代码,python没有也就算了,俩matlab都找不到,找到了还要钱,好家伙,看不起谁丫?!虽然有一些python的智能算法库,但是要么就是集成的太多,没有专门正对PSO的一些变体进行集成,虽然有一个专门搞PSO的库,但是,那玩意就集成了一个算法,核心文件就一个PSO。
所以,既然没有,那么我就自己造个轮子先看看,而且我觉得,如果论文没给代码的,我觉得这种论文要么就是有鬼,要么就是S13写的,少看,那些期刊的评审真的也需要擦亮眼睛看看,连代码连接都不敢给的论文,有啥好评审的。
目前先搞一个最简单的版本,不过目前是只有集成到PSO的,而且目前是针对单目标平台的,多目标的话有PlatEMO,所以基本上不太需要我再写一个,只是单目标的话我是没找到合适的,那些论文的作者也没给代码,网上资源也少,不知道是太简单了还是怕露馅了,毫无开源精神。
版权
郑重提示:本文版权归本人所有,任何人不得抄袭,搬运,使用需征得本人同意!
2022.7.4
日期:2022.7.4
集成算法
目前的话,这个玩意是集成了PSO的算法,其中PSO的算法分为两大类,一个是基于参数优化的算法,另一个是多种群策略,本来我还想搞几个优化拓扑结构的来的,但是一方面是实现的问题,另一方面是论文没说明白(中文的)英文的要时间,我没那么多时间搞这个破玩意,因为自己的算法还没做完,我只是想要一个对比测试的东东。
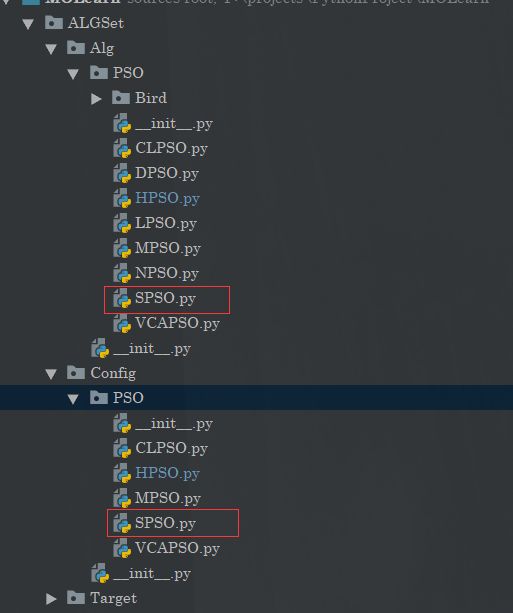
项目结构
基本粒子群算法SPSO
数据结构
import random
from ALGSet.Config.PSO.SPSO import *
class SBird(object):
#这个是从1开始的
ID = 1
Y = None
X = None
V = None
PbestY = None
PBestX = None
GBestX = None
GBestY = None
def __init__(self,ID):
self.ID = ID
self.V = [random.random() *(V_max-V_min) + V_min for _ in range(DIM)]
self.X = [random.random() *(X_up-X_down) + X_down for _ in range(DIM)]
def __str__(self):
return "ID:"+str(self.ID)+" -Fintess:%.2e:"%(self.Y)+" -X"+str(self.X)+" -PBestFitness:%.2e"%(self.PbestY)+" -PBestX:"+str(self.PBestX)+\
"\n -GBestFitness:%.2e"%(self.GBestY)+" -GBestX:"+str(self.GBestX)
相关配置
配置也是和算法的名称对应的,在上面的图也能够看出来。
#coding=utf-8
# 相关参数的设置通过配置中心完成
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
C1=1.458
C2=1.458
W = 0.72
m = 3
DIM = 10
PopulationSize=30
#运行1000次(可以理解为训练1次这个粒子群要跑一千次)
IterationsNumber = 3000
X_down = -10.0
X_up = 10
V_min = -5.0
V_max = 5
Wmax = 0.9
Wmin = 0.4
def LinearW(iterate):
#传入迭代次数
w = Wmax-(iterate*((Wmax-Wmin)/IterationsNumber))
return w
def Dw(iterate):
w = Wmax-((iterate**2)*((Wmax-Wmin)/(IterationsNumber**2)))
return w
def Nw(iterate):
w = Wmin+(Wmax-Wmin)*(((IterationsNumber-iterate)**m)/(IterationsNumber**m))
return w
实现代码
#coding=utf-8
#这个是最基础的PSO算法SPSO算法
import sys
import os
from ALGSet.Alg.PSO.Bird.SBird import SBird
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
from ALGSet.Target.Target import Target
from ALGSet.Config.PSO.SPSO import *
import random
import time
class SPso(object):
Population = None
Random = random.random
target = Target()
W = W
def __init__(self):
#为了方便,我们这边直接先从1开始
self.Population = [SBird(ID) for ID in range(1,PopulationSize+1)]
def ComputeV(self,bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i])
#这里注意判断是否超出了范围
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:SBird):
NewX = []
NewV = self.ComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i]+NewV[i]
if(x>X_up):
x = X_up
elif(x<X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
def Running(self):
#这里开始进入迭代运算
for iterate in range(1,IterationsNumber+1):
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
if __name__ == '__main__':
start = time.time()
sPSO = SPso()
sPSO.InitPopulation()
sPSO.Running()
end = time.time()
print("Y: ",sPSO.Population[0].GBestY)
print("X: ",sPSO.Population[0].GBestX)
print("花费时长:",end-start)
目标函数
目标函数的话其实都在Target里面
目前的话其实还是在做算法的集成,里面的很多东西其实压根没怎么架构,不过这个后面改起来很快。现在先把一些算法塞进去。
import math
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
class Target(object):
def SquareSum(self,X):
res = 0
for x in X:
res+=x*x
return res
参数优化(单种群)PSO系列算法
我们在这边其实是集成了三个
LPSO
这个其实就是线性变化权重。
"""
LPSO:这个玩意其实还只是对W进行优化了
"""
import time
from ALGSet.Alg.PSO.SPSO import SPso
from ALGSet.Config.PSO.SPSO import *
class LPso(SPso):
def Running(self):
# 这里开始进入迭代运算
for iterate in range(1, IterationsNumber + 1):
# 这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
w = LinearW(iterate)
self.W = w
for bird in self.Population:
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
bird.X = x
bird.Y = y
if (bird.Y <= bird.PbestY):
bird.PBestX = bird.X
bird.PbestY = bird.Y
# 个体中的最优一定包含了全局经历过的最优值
if (bird.PbestY <= Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
if __name__ == '__main__':
start = time.time()
lPSO = LPso()
lPSO.InitPopulation()
lPSO.Running()
end = time.time()
print("Y: ",lPSO.Population[0].GBestY)
print("X: ",lPSO.Population[0].GBestX)
print("花费时长:",end-start)
DPSO
这个其实就是把线性权重变成了这个玩意
def Dw(iterate):
w = Wmax-((iterate**2)*((Wmax-Wmin)/(IterationsNumber**2)))
return w
代码其实就是把刚刚的WLinear变成了Dw
NPSO
同理,w函数变成这个了。
def Nw(iterate):
w = Wmin+(Wmax-Wmin)*(((IterationsNumber-iterate)**m)/(IterationsNumber**m))
return w
自适应PSO(VCAPSO)
这个算法的实现相对复杂一点,其实也不难。
具体资料的话自己感兴趣可以去查查,我这里还没整理好,就不发了。
参数配置
这个的话也是在Config那个包下面的
#coding=utf-8
# 相关参数的设置通过配置中心完成
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
C1=1.458
C2=1.458
K1 = 0.72
K2 = 0.9
DIM = 10
PopulationSize=30
IterationsNumber = 3000
X_down = -10.0
X_up = 10
V_min = -5.0
V_max = 5
Wmax = 0.9
Wmin = 0.4
核心代码
"""
这个算法其实也是关于参数进行了优化的
基于云自适应算法进行适应的(什么叫做云我也不懂,不过公式给我就好了)
"""
import math
import time
import random
from ALGSet.Alg.PSO.SPSO import SPso
from ALGSet.Config.PSO.VCAPSO import *
class VCAPso(SPso):
F_avg = 0.
F_avg1=0.
F_avg2=0.
En = 0.
He = 0.
def InitPopulation(self):
#初始化种群
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
self.F_avg+=bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
self.F_avg/=PopulationSize
self.En = (self.F_avg-Flag)/C1
self.He = self.En/C2
self.En = random.uniform(self.En,self.He)
self.F_avg1,self.F_avg2 = self.__GetAvg2(self.Population)
def ComputeV(self,bird):
#这个方法是用来计算速度滴
NewV=[]
if(bird.Y<=self.F_avg1):
w = K1
elif(bird.Y>=self.F_avg2):
w = K2
else:
w = Wmax-Wmin*(math.exp(-((bird.Y-self.En)**2)/(2*(self.En**2))))
for i in range(DIM):
v = bird.V[i]*w + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i])
#这里注意判断是否超出了范围
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def __GetAvg2(self,Population):
F_avg1 = 0.
F_avg2 = 0.
F_avg1_index = 0
F_avg2_index = 0
for bird in Population:
if(bird.Y<self.F_avg):
F_avg1_index+=1
F_avg1+=bird.Y
elif(bird.Y>self.F_avg):
F_avg2_index+=1
F_avg2+=bird.Y
if (not F_avg1_index == 0):
F_avg1 /= F_avg1_index
else:
F_avg1 = float("inf")
if (not F_avg2_index == 0):
F_avg2 /= F_avg2_index
else:
F_avg2 = float("inf")
return F_avg1,F_avg2
def Running(self):
# 这里开始进入迭代运算
for iterate in range(1, IterationsNumber + 1):
# 这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
F_avg = 0.
for bird in self.Population:
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
bird.X = x
bird.Y = y
F_avg += bird.Y
if (bird.Y <= bird.PbestY):
bird.PBestX = bird.X
bird.PbestY = bird.Y
# 个体中的最优一定包含了全局经历过的最优值
if (bird.PbestY <= Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
self.F_avg = F_avg
self.F_avg /= PopulationSize
self.En = (self.F_avg - Flag) / C1
self.He = self.En / C2
self.En = random.uniform(self.En, self.He)
self.F_avg1, self.F_avg2 = self.__GetAvg2(self.Population)
if __name__ == '__main__':
start = time.time()
vcaPso = VCAPso()
vcaPso.InitPopulation()
vcaPso.Running()
end = time.time()
print("Y: ", vcaPso.Population[0].GBestY)
print("X: ", vcaPso.Population[0].GBestX)
print("花费时长:", end - start)
综合粒子群算法(CLPSO)
这个算法是在原来那篇论文里面提到的,先去复现的时候也是复现了的其实,现在只是单独提取出来罢了。
值得一提的是,这个玩意其实设计出来主要是应对多峰函数的,收敛也较慢。
import math
import time
from ALGSet.Target.Target import Target
from ALGSet.Config.PSO.CLPSO import *
from ALGSet.Alg.PSO.Bird.CLBird import CLBird
import random
class CLPso(object):
Population = None
Random = random.random
target = Target()
W = 0.
Math = math
def __init__(self):
#为了方便,我们这边直接先从1开始
self.Population = [CLBird(ID) for ID in range(1,PopulationSize+1)]
def __PCi(self,i,ps):
"""
论文当中的PCi的算子
:return:
"""
pci = 0.05+0.45*((self.Math.exp(10*(i-1)/(ps-1)))/(self.Math.exp(10)-1))
return pci
def NewComputeV(self, bird):
"""
:param bird:
:param params: 传入的数据格式为:[[w,c1,c2,c3],[],[],[],[]] 这里一共是5组共设置100个粒子
:return:
这里按照ID的顺序来调用不同的参数
"""
NewV = []
for i in range(DIM):
v = bird.V[i] * self.W
if (self.Random() < self.__PCi((i + 1), PopulationSize)):
pbestfi = bird.Follow.PBestX[i]
else:
pbestfi = bird.PBestX[i]
v = v + C1 * self.Random() * (pbestfi - bird.X[i])
if (v > V_max):
v = V_max
elif (v < V_min):
v = V_min
NewV.append(v)
return NewV
def NewComputeX(self, bird: CLBird):
NewX = []
NewV = self.NewComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i] + NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群,不过是给ENV调用的,因为这个里面有一个CLPSO的思想
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
#便利了一遍我们得到了全局最优的种群
self.GBestY = Flag
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
#现在是初始化,所以这个这样算是没问题的
self.GBestYLast = Flag
#给每一个粒子找到一个追随者
self.ChangeBird(bird,self.Population)
def ChangeBird(self,bird,Population):
#这个主要是实现锦标赛法来对粒子的跟踪对象进行更新
while True:
#被跟踪的粒子不能和自己一样,也不能和上一个一样
a,b = random.sample(range(PopulationSize),2)
a = Population[a];b=Population[b]
follow = a
if(a.PbestY>b.PbestY):
follow = b
if(follow.ID!=bird.ID):
if(bird.Follow):
if(bird.Follow.ID !=follow.ID):
bird.Follow = follow
return
else:
bird.Follow = follow
return
def Running(self):
for iterate in range(1,IterationsNumber+1):
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
self.W = LinearW(iterate)
for bird in self.Population:
x = self.NewComputeX(bird)
y = self.target.SquareSum(x)
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
elif (bird.Y == bird.PbestY):
bird.NoChange += 1
if (bird.NoChange == M_follow):
self.ChangeBird(bird, self.Population)
bird.NoChange = 0
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
if __name__ == '__main__':
start = time.time()
clPSO = CLPso()
clPSO.InitPopulation()
clPSO.Running()
end = time.time()
print("Y: ",clPSO.Population[0].GBestY)
print("X: ",clPSO.Population[0].GBestX)
print("花费时长:",end-start)
多种群算法
MPSO 算法
这个算法就是分三个种群,然后,一个执行LPSO,一个执行SPSO,还一个执行VCAPSO。
这个就是集成三个算法,然后改了一些速度方程。
v = bird.V[i] * w + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \
+ C2*self.Random()*(bird.CBestX[i]-bird.X[i])\
+C3*self.Random()*(self.GBestX[i]-bird.X[i])
HPSO算法
这个就是混合多种群PSO。也是代码很简单,而且是目前测试效果最好的。
import random
import time
from ALGSet.Alg.PSO.Bird.Hbird import HBird
from ALGSet.Config.PSO.HPSO import *
from ALGSet.Target.Target import Target
class HPso():
rand = random.random
miu = miu
target = Target()
def __init__(self):
self.Population = [HBird(ID) for ID in range(1,PopulationSize+1)]
self.Divide()
def Divide(self):
#我们这边直接通过ID进行分类
CID = 0
for bird in self.Population:
bird.CID=CID
if(bird.ID % ClusterSize==0):
if(CID<=ClusterNumber):
CID+=1
def ComputeV(self,bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
v1 = bird.V[i] * self.W + C1 * self.rand() * (bird.PBestX[i] - bird.X[i]) \
+ C2 * self.rand() * (bird.GBestX[i] - bird.X[i])
v2 = bird.V[i] * self.W + C1 * self.rand() * (bird.PBestX[i] - bird.X[i]) \
+ C2 * self.rand() * (bird.CBestX[i] - bird.X[i])
v = v1*self.miu+(1-self.miu)*v2
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird):
NewX = []
NewV = self.ComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i]+NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群
#这个是记录全局最优解的
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
#还有一个是记录Cluster最优解的
CBest = {}
CFlag = {}
for i in range(ClusterNumber):
CFlag[i]=float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
bird.CBestX = bird.X
bird.CBestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
if(bird.Y<=CFlag.get(bird.CID)):
CBest[bird.CID]=bird.X
CFlag[bird.CID] = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
bird.CBestY=CFlag.get(bird.CID)
bird.CBestX=CBest.get(bird.CID)
def Running(self):
#这里开始进入迭代运算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
CBest = {}
CFlag = {}
for i in range(ClusterNumber):
CFlag[i] = float("inf")
for bird in self.Population:
#更改为线性权重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
if (bird.Y <= CFlag.get(bird.CID)):
CBest[bird.CID] = bird.X
CFlag[bird.CID] = bird.Y
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
bird.CBestY = CFlag.get(bird.CID)
bird.CBestX = CBest.get(bird.CID)
if __name__ == '__main__':
start = time.time()
hPso = HPso()
hPso.InitPopulation()
hPso.Running()
end = time.time()
print("Y: ", hPso.Population[0].GBestY)
print("X: ", hPso.Population[0].GBestX)
print("花费时长:", end - start)
后续工作
搞可视化测试,后面,不过,这个要后面在做,代码后面上传。