关于有向图强连通分量 和 无向图双联通分量的理解

有向图的强连通分量
1.强连通 代表的是 这个连通块中的每两个点互相都是有一条路径是可以走到的
2.分量 就是子图；

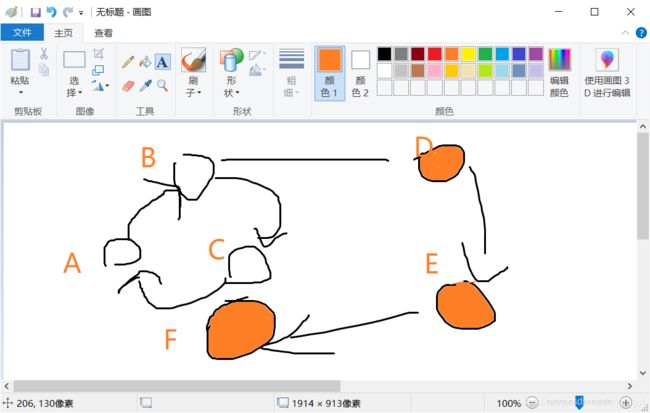
从这张图上可以看出 A B C这三个点都是互相可以走到的 所以他们就是一个联通块 D E F 三个点都是单向能走到 所以D E F 分别为三个联通分量
所以这个图中 一共有 四 个连通分量
然后又引入一个概念 缩点 将连通块中的点当成一个点
可以用来求 连通块问题

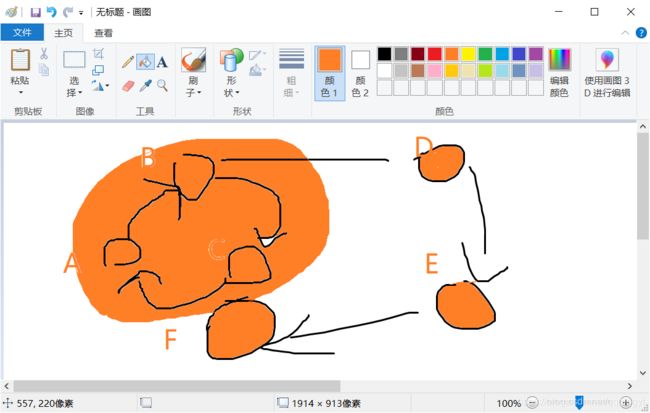
我们知道概念了 该如何去求这个图中有几个连通分量呢
引用时间戳这个概念
A - > B -> D -> E -> F
A -> B -> C
所以ABCDEF的进入时间分别为1 2 6 3 4 5
我们走到 F的时候 发现没有路可以走了 所以没有形成 一个环所以 他自成一个 E D 分别自成一个 走到 C的时候发现可以回到 1 所以他是可以和 A成一个环的 所以 把C的时间戳修改成 A的时间戳 表明 他们是可以走一起的 同样返回的时候 把 B 的时间戳也修改成 与 C已经成功成环的时间戳 即可

#include
#include

using namespace std;

const int N = 1e4 + 10,M = 5e4 + 10;

int head[N],to[M],last[M],cnt;
void add(int a,int b){
	to[++cnt] = b;
	last[cnt] = head[a];
	head[a] = cnt;
}

int n,m;
int toopc[N];
int dfn[N],low[N],sta[N],top,ttime,flag[N],scc_cnt,st_size[N],belong[N];
void dfs(int x){
	dfn[x] = low[x] = ++ttime; //两个时间戳 一个记录进入时间 一个记录最后是否是一个时间戳的时间
	sta[++top] = x,flag[x] = 1; //记录这个路径中的点
	for(int i = head[x]; i != -1; i = last[i]){
		int j = to[i];
		if(!dfn[j]){ 
			dfs(j);
			low[x] = min(low[x],low[j]); //变成 下一个点已经成环的时间戳
		}else if(dfn[j] && flag[j]){
			low[x] = min(low[x],dfn[j]); //如果此次路劲已经走过了他 那么直接判断即可
		}
	}
	
	if(low[x] == dfn[x]){ //如果时间戳相同的话 那么这个点就是这个环的起点位置
		++scc_cnt; 
		int y;
		int h = 0;
		do{
			++h;
			y = sta[top--];
			flag[y] = 0;
			belong[y] = scc_cnt; //这个点属于这个环
		}while(y != x);
		st_size[scc_cnt] = h;
	}
}

int main(){
	memset(head,-1,sizeof head);
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		int x,y;
		cin >> x >> y;
		add(x,y);
	}
	
	for(int i = 1; i <= n; i++){
		if(!dfn[i]) dfs(i);
	}	
	
	for(int i = 1; i <= n; i++){
		for(int j = head[i]; j != -1; j = last[j]){
			int k = to[j];
			if(belong[i] != belong[k]){
				toopc[belong[i]]++;
			}
		}
	}
	
	int sum = 0;int s = 0;
	for(int i = 1; i <= scc_cnt; i++){
		if(toopc[i] == 0){
			sum += st_size[i];
			++s;
		}
		if(s > 1){
			sum = 0;
		}
	}
	
	cout << sum << endl;
	return 0;
}

双连通分量指的是 连通块中的每两个点都有 两条不相交的路径可以走到对方
而去掉图中的一条边 使连通块增加的这个边 叫做桥

去掉 全部与一个点的边 使连通块数量增加的点 叫割点

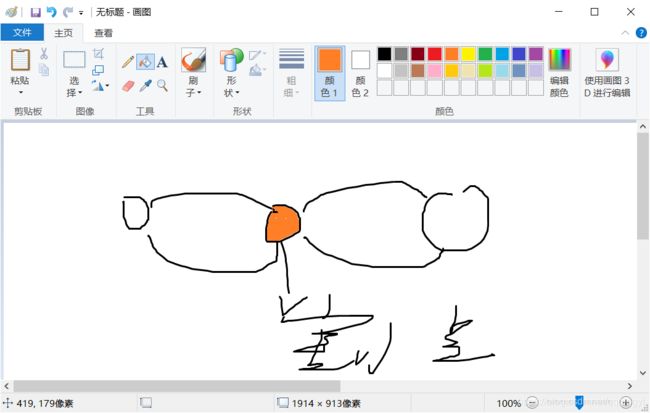
红色的点就是割点

如何去求一个图中的桥呢

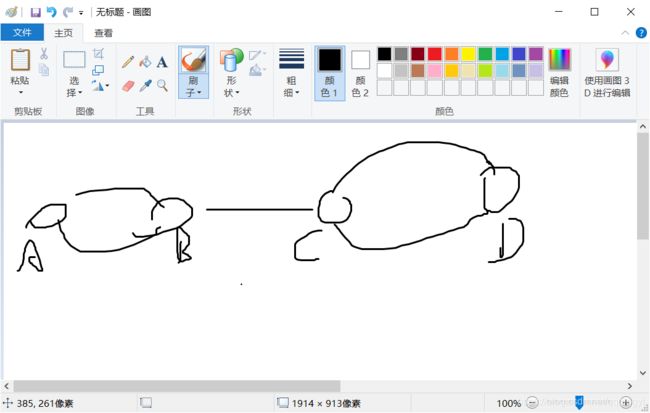
由图推导
A->B->C->D->C 所以C和D是一个环 是一个联通块
但是C -> B 是B -> C 的反向边 所以 C->B不能使ABCD成为同一个双连通块
所以 这个时候 B->C就成为了一个桥同样B->C也是一个桥 所以当
这条边无法是他们成为同一个连通块的时候 就是一个桥；

#include
#include 

using namespace std;

const int N = 1e4 + 10,M = 1e5 + 10;

int n,m;
int head[N],to[M],last[M],cnt;
void add(int a,int b){
	to[cnt] = b;
	last[cnt] = head[a];
	head[a] = cnt++;
}

int dfn[N],low[N],sta[N],is_bridge[N],belong[N],toop[N];
int times,top,scc_cnt;
void tarjan(int x,int lastt){
	dfn[x] = low[x] = ++times;
	sta[++top] = x;
	for(int i = head[x]; i != -1; i = last[i]){
		int j = to[i];
		if(!dfn[j]){
			tarjan(j,i);
			low[x] = min(low[x],low[j]);
			if(dfn[x] < low[j]){ // 如果low[j] > dfn[x] 说明 j 和 x点不是同一连通分量 
				is_bridge[i] = is_bridge[i ^ 1] = 1;
			}
		}else if(i != (lastt ^ 1)){ //由于是无向图所以 i + 1 是 i 的反向边 如果 i % 2 == 0 
			low[x] = min(low[x],dfn[j]);  //如果不判断反向边的话 dfn[x] == low[j] 
		}
	}
	if(dfn[x] == low[x]){
		++scc_cnt;
		int y;
		do{
			y = sta[top--];
			belong[y] = scc_cnt;
		}while(y != x);
	} 
}

int main(){
	memset(head,-1,sizeof head);
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		int x,y;
		cin >> x >> y;
		add(x,y);
		add(y,x);
	}
	
	tarjan(1,-1);
	
	for(int i = 0; i < cnt; i++){
		if(is_bridge[i]){
			toop[belong[to[i]]]++;
		}
	}
	
	int ans = 0;
	for(int i = 1; i <= scc_cnt; i++){
		if(toop[i] == 1){
			ans++;
		}
	} 
	
	cout << (ans + 1) / 2 << endl;
	
	
	return 0;
} 

割点怎么求；
我们照样可以用图来推导

C ->B -> A
我们发现 A自成了一个连通分量 所以A只能 通过 B才能返回到原来的祖先
所以B就是一个割点
同样如果A B 成环的话 A 还是得需要从B才能回到C 所以B还是割点
所以当dfn[i] <= low[j]的时候 那么B就是一个割点

#include
#include
#include

using namespace std;

const int N = 1010;
int n,maxn;

int head[N],to[N * 2],last[N * 2],cnt;
void add(int a,int b){
	to[++cnt] = b;
	last[cnt] = head[a];
	head[a] = cnt;
}

vector<int>dcc[N];
int dfn[N],low[N],sta[N],cut[N];
int times,top,root,dcc_cnt;
void tarjan(int x){
	dfn[x] = low[x] = ++times;
	sta[++top] = x;
	int ans = 0;
	if(x == root && head[x] == -1){
		++dcc_cnt;
		dcc[dcc_cnt].push_back(x);
		return; 
	}
	
	for(int i = head[x]; i != -1; i = last[i]){
		int j = to[i];
		if(!dfn[j]){
			tarjan(j);
			low[x] = min(low[x],low[j]);
			if(dfn[x] <= low[j]){
				ans++;
				if(x != root || ans > 1) cut[x] = 1; //如果他是根节点的话那么他就没有祖先所以 只有他有两个儿子节点才能变成割点
				++dcc_cnt;
				int y;
				do{
					y = sta[top--];
					dcc[dcc_cnt].push_back(y);//将割点影响到的点记录下来
				}while(y != j); //如果y != x的话 那么割点x就没了，那么后续如果还有连通分量的话 就不成立了
				dcc[dcc_cnt].push_back(x); 
			}
		}else low[x] = min(low[x],dfn[j]);
	}
}

int main(){
	int casse = 0;
	while(cin >> n && n){
		memset(head,-1,sizeof head);
		memset(dfn,0,sizeof dfn);
		memset(cut,0,sizeof cut);
		maxn = 0,cnt = 0;
		dcc_cnt = 0,times = 0,top = 0;
		for(int i = 1; i <= n; i++){
			int x,y;
			cin >> x >> y;
			maxn = max(maxn,x);
			maxn = max(maxn,y);
			add(x,y);
			add(y,x);
		}
		
		for(root = 1; root <= maxn; root++){
			if(!dfn[root]){
				tarjan(root);
			}
		}
		
		int sum = 0;
		for(int i = 1; i <= maxn; i++){
			if(cut[i] == 1) sum++;
		}
		
		cout << sum << endl;
	}
	return 0;
}