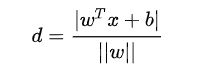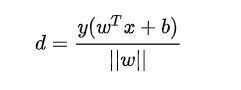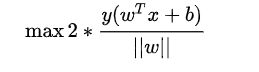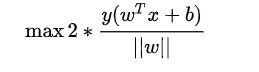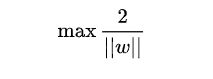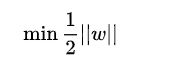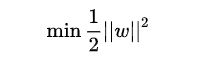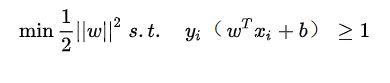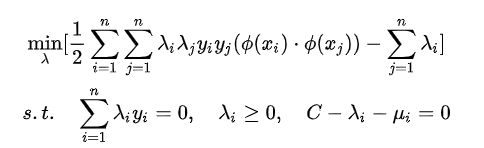简单点理解 SVM（支持向量机）

1、SVM简介

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。可能不好理解，那我们来举个例子吧

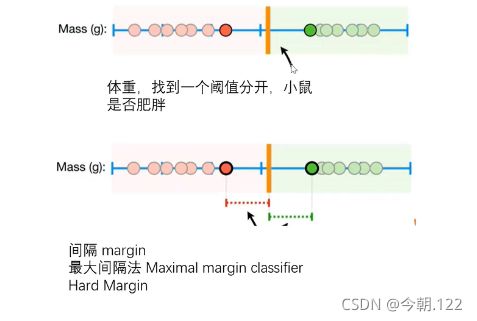
根据体重判断小鼠是否肥胖，首先得找到一个阈值，这个阈值怎么找呢？按从小到大的顺序排列后找到间隔最大的俩只小鼠取它们的中间体重，这个就是阈值。

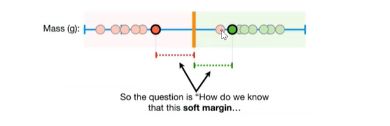
但是也可能出现误差

 

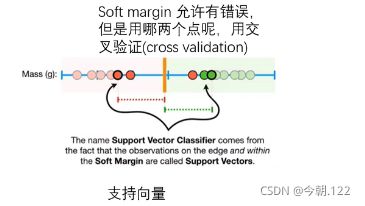
 （其中粉色代表肥胖，绿色代表不肥胖）这个图中个别案例不符合最大间隔法，所以这时就需要用到Sort Margin，如图

 2、SVM算法简介

 2.1、最大间隔法介绍：

                   

具体方法如下：

每个支持向量到超平面的距离可以写为：

由上述 

 可以得到 

 ，所以我们得到：

最大化这个距离：

                                        

这里乘上 2 倍也是为了后面推导，对目标函数没有影响。刚刚我们得到支持向量  

     ， 

 ，所以我们得到：

再做一个转换：

为了方便计算（去除 ||w|| 的根号），我们有：

所以得到的最优化问题是：

 若要求解上面那个方程就必须用到拉格朗日乘子法，然后就会把一个含有约束的问题转化为没有约束的的问题，然后再转为对偶问题，最后转化为反对偶问题

           

 接下来就是对了L(w,b,a)求偏导，这里我就不一一证明了，最后得到一个结果

 转化为对求最大，最重要的是不要忘了新增的条件

 补（对偶问题证明：强对偶性、弱对偶性以及KKT条件的证明（对偶问题的几何证明）_Cyril_KI的博客-CSDN博客这个博客讲的很透彻）

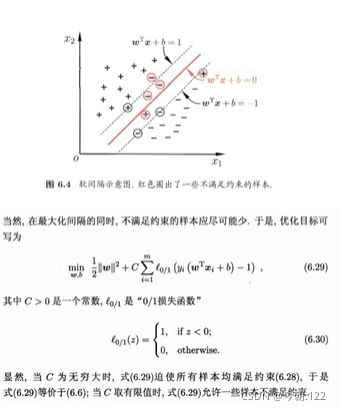
  2.2、Soft Margin

 当C是无穷大时，式子6.29要想取得最小值，那后面部分必须是0，所以全部满足条件

当C是有限值时，式子6.29要想取得最小值，可能后面那一部分不为0，所以可以有部分样本不满足约束

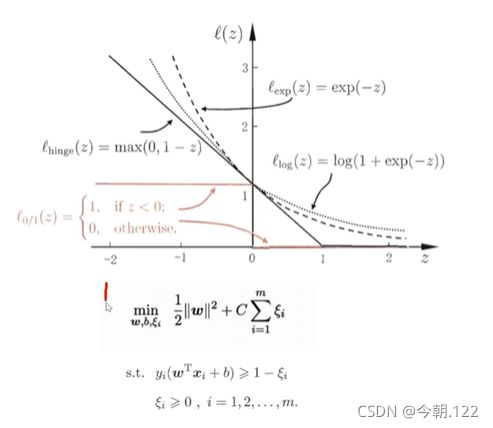
 上图中的loss函数有多种，例如：

 推荐使用下面一个，因为上面那个函数不连续

然后就可以画出Sort Marg示例图，如图：

 2.3、SMO算法

SMO(Sequential Minimal Optimization)，序列最小优化算法，其核心思想非常简单：每次只优化一个参数，其他参数先固定住，仅求当前这个优化参数的极值。下面这篇博客将带您认识什么是SMO算法

2.4、核函数

2.4.1 线性不可分

我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。

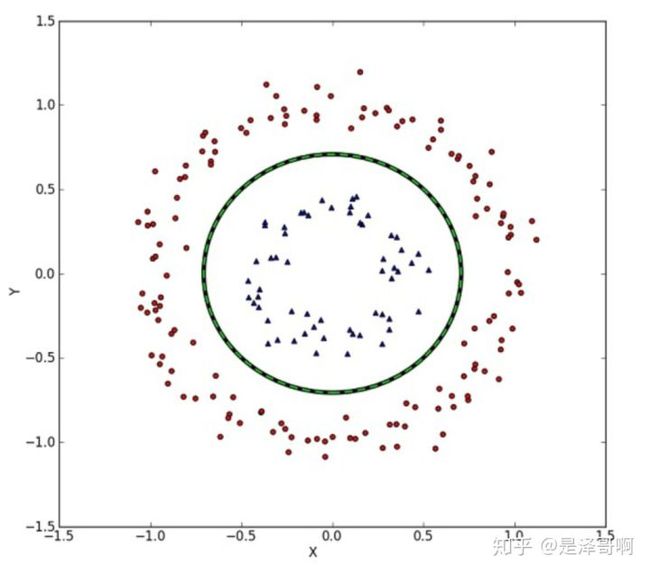
但我们可能会碰到的一种情况是样本点不是线性可分的，比如：

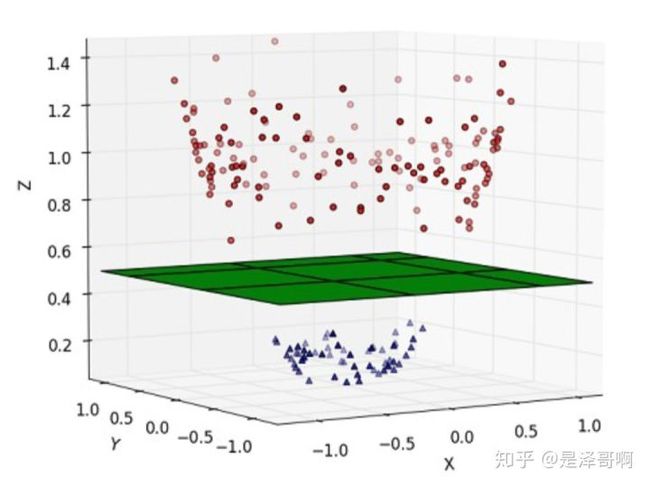
这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，比如：

对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。我们用 x 表示原来的样本点，用  

 表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为： 

。

对于非线性 SVM 的对偶问题就变成了：

 

 2.4.2、核函数的作用

我们不禁有个疑问：只是做个内积运算，为什么要有核函数的呢？

这是因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。

 2.4.3、常见的核函数

3、用python实现svm计算

首先将需要使用的包导进来

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt

紧接着就是准备训练样本和生成随机试验数据

​
x = [[1, 8], [3, 20], [1, 15], [3, 35], [5, 35], [4, 40], [7, 80], [6, 49]]
y = [1, 1, -1, -1, 1, -1, -1, 1]

#这里是15行2列​
rdm_arr = np.random.randint(1, 15, size=(15, 2))

下面就是最关键的选择核函数了

常见的核函数有：

​
'''
​
'''h度多项式核函数（Polynomial Kernel of Degree h）
 clf = svm.SVC(kernel='linear').fit(x, y)

高斯径向基和函数（Gaussian radial basis function Kernel）
clf = svm.SVC(kernel='rbf').fit(x, y)

S型核函数（Sigmoid function Kernel）
clf = svm.SVC(kernel='sigmoid').fit(x, y)

图像分类，通常使用高斯径向基和函数，因为分类较为平滑，
文字不适用高斯径向基和函数。没有标准的答案，可以尝试各种核函数，根据精确度判定。'''

​
'''

​

接下来就是绘制样本点；

    for i in x:
        ax.set_title(titles[tn])
        res = clf.predict(np.array(i).reshape(1, -1))
        if res > 0:
            ax.scatter(i[0], i[1], c='r', marker='*')
        else:
            ax.scatter(i[0], i[1], c='g', marker='*')
    '''绘制实验点'''
    for i in rdm_arr:
        res = clf.predict(np.array(i).reshape(1, -1))
        if res > 0:
            ax.scatter(i[0], i[1], c='r', marker='.')
        else:
            ax.scatter(i[0], i[1], c='g', marker='.')

最后是绘制图形

plt.show()