感知机原理以及python实现

感知机

  感知机是一个二分类的线性分类模型，输入数据为实例的特征向量，输出为实例的分类，输出取+1和-1两个值。感知机是一个分类模型，旨在找出一个超平面，这个超平面能够正确的将输入数据分类。感知机是支持向量机和神经网络的基础。

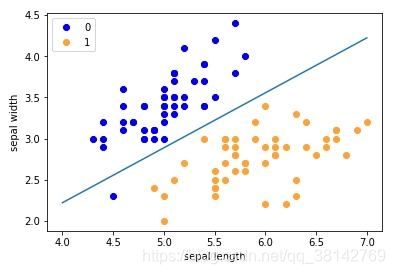
感知机的定义

  假设 $x$ 表示为实例的特征向量，对应于输入空间的一个点，输出空间 $f(x)$ 表示 $x$ 的类别，那么从 $x$ 到 $f(x)$ 的映射可以写为：

$$f(x)=sign(w\cdot x+b)$$
  从输入空间到输出空间的映射称之为感知机，其中 $x$ 表示为输入空间的一个实例，$w$ 和 $b$ 为感知机的参数，$w$ 相当于实例 $x$ 的系数，也叫做权值。$b\in R$ 叫做偏移量。$sign$ 函数即为常见的+1 和 -1的判断函数。

数据的线性可分

  给定一个数据集 T
$$T=[（x_1,y_1),(x_2,y_2),....,(x_n,y_n）]$$
  如果存在一个超平面，可以将数据集 T 中所有的向量完全正确的划分在超平面的两侧。那么就称这个数据集线性可分，否则，线性不可分。

损失函数

  假设一个数据集 T 是线性可分的，根据我们的数据，要寻找出一个能够将数据完全正确划分开的超平面。感知机的映射函数为
$$f(x)=sign(w\cdot x+b)$$
  也就是我们需要确定$f(x)$ 中$w$ 和 $b$ 的值。因此我们需要采取一个方法，即定义一个损失函数，并将损失函数极小化。
 损失函数的一个选择方法是选择误分类的点数。但是不能根据这样的方式推导出$w$ 和 $b$ 的值。另一个方法是选择误分类点到超平面$S$的距离。一个点$x_0$到超平面$S$的距离为：
$$\frac{1}{||w||}|w\cdot x_0+b|$$
  因为错误分类的点到超平面的距离与将改错误点正确分类到超平面的距离总是相反的，所以误分类的点到超平面的距离则是：
$$-\frac{1}{||w||}{y}_0(w\cdot x_0+b)$$
  假设分类错误的点的个数为N，因此所有错误的点到超平面的距离可以表示为：

$$-\frac{1}{||w||}\sum _{i=1}^N{y}_i(w\cdot x_i+b)$$
这里对$$\frac{1}{||w||}$$进行删除的话，就得到了感知机的损失函数：
$$L（w,b）=-\sum _{i=1}^N{y}_i(w\cdot x_i+b)$$
  删除的原因一方面是我们追求的是损失函数为0的情况下的$w$ 和 $b$
根据这个式子我们可以看出来，如果错误分类的数量为0，那么损失函数也为0，所以和系数没有多大的关系。并不影响最终结果。并且损失函数始终为正。并且损失函数为连续可导函数。

感知机的原始算法

给定一个数据集
$$T=[（x_1,y_1),(x_2,y_2),....,(x_n,y_n）]$$
给定一个学习率$\eta$(0 < $\eta$ < 1)

1. 对$w$ 和 $b$ 赋初始值 $w_0$ 和 $b_0$
2. 选取一个数据点$(x_i,y_i)$，并判断是否分类正确。根据公式$y_I(w\ast x_i+b)$ 和0的大小来进行判断，大于0则分类正确。 如果分类错误
3. 就对$w$ 和 $b$进行更新，公式为：
   $w=w+\eta x_i{y}_i$
   $b=b+\eta y_i$
4. 重复步骤2和步骤3，直到没有错误分类点。
5. 最后我们就得到了感知机的参数$w$ 和 $b$

原始算法的例题

有$x_1=(3,3),y_1=1,x_2=(4,3),y_2=1,x_3=(1,1),y_1=-1$组成的数据集$T=\{(x_1{y}_1),(x_2,y_2),(x_3,y_3)\}$
试构建感知机原始算法模型

1. 对 $w$ 和 $b$ 赋初值为$w_0=0,b_0=0$。对 $\eta$ 赋初值为 1.
2. 选取数据点$(x_1,y_1)$，判断是否分类正确。
   $y_1(w_0\ast x_1+b_0)=0$ 分类错误
3. 对$w$ 和 $b$进行更新：
   $w_1=w_0+\eta x_1{y}_1=(3,3)$
   $b_1=b_0+\eta y_1=1$
4. 对$x_1，x_2$进行判断，因为$y_2(w_1\ast x_2+b_1)>0,y_1(w_1\ast x_1+b_1)>0$所以这两个分类正确。
5. 对$x_3$进行判断，因为
   $y_3(w_1\ast x_3+b_1)<0$ 所以第三个数分类错误。
6. 对$w$ 和 $b$进行更新：
   $w_2=w_1+\eta x_3{y}_3=(2,2)$
   $b_2=b_1+\eta y_3=0$
7. 然后重复检查$x_3$，直到$x_3$套入公式后>0,然后重复步骤2-6。直到所有数据全部分类正确。
8. 最终结果为 $w_7=(1,1),b=-3$ 。

感知机原始算法的对偶形式

  在上面感知机的算法原理求解例题过程中，可以发现会检查很多次是否正确分类。假设修改了n次，则$w,b$ 每次修改的增量为${\alpha }_i{y}_i{x}_i$ 和 ${\alpha }_i{y}_i$ , 因为$\eta$ 为常数，所以整合为 $\alpha$ ,即${\alpha }_i=n{\eta }_i$。那么最终的$w,b$ 可以分别表示为：
$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$
$$b=\sum _{i=1}^N{\alpha }_i{y}_i$$
那么最终，感知机的对偶形式可以变化为:
$$f(x)=sign(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b)$$
这里用$j$不用$i$是因为要区分数据集中的$i$

对偶形式的算法过程

1. 对$\alpha$ 和 $b$ 赋值为 0
2. 选取数据集的$(x_i,y_i)$
3. 如果 $y_i({\sum }_{j=1}^N{\alpha }_j{x}_j{y}_j\cdot x_i+b)\le 0$
   $${\alpha }_i={\alpha }_i+\eta$$
   $$b=b+\eta y_i$$
4. 重复步骤2-3 直到没有误分类数据。

对偶形式的优点

 假设按照感知机原始形式所有的参数更新一共需要n次，对偶形式就是把这n次分摊到i个样本中去，这样最终的参数可以展开使用每个样本点进行表示，这样在判断误分类的时候的计算就都可以展开成样本之间的点乘形式，这样就可以通过提前算好的Gram矩阵来大大降低计算量，因为仅仅计算了一次，后续全部通过查表就可以了。而反观原始形式，每次参数改变，所有的矩阵计算全部需要计算，导致计算量比对偶形式要大很多。

感知机算法的python实现

import numpy as np 
import matplotlib.pyplot as plt 
import time

def check(x,y,w,b): # 检查是否正确分类
    wx = w * x
    wx = sum(wx)
    result = y * (wx + b)
    if result > 0:
        return True
    else:
        return False

def regirt(x,y,n,w,b):# 将w， b 进行更新
    w = w + n*x*y
    b = b + n*y
    return w, b

def find_all(x_data, y_data, w, b): # 感知机流程
    data_len = len(x_data)
    i = 0
    while(i<data_len):
        print('正在测试',x_data[i], y_data[i])
        if check(x_data[i], y_data[i], w, b) == True:
            print(x_data[i], y_data[i], '分类正确')
            i += 1
        else:
            print( sum((w * x_data[i] + b) * y_data[i]), '< 0 ')
            w, b = regirt(x_data[i], y_data[i], n, w, b)
            print( 'w b 更新为:',w,b);
            i = 0
        print("\n")
    print('最终的w b 为:', w, b)
    return w, b 


if __name__ == "__main__":
    x_data = np.array([[3,3],[4,3],[1,1]])
    y_data = np.array([1,1,-1])
    w = 0
    b = 0
    n = 1
    find_all(x_data,y_data, w, b)

线性可分与凸壳

这里可以参考其他的博客，内容过多，以后再做详解。
https://blog.csdn.net/y954877035/article/details/52210734

参考资料

参考资料
[1]:https://www.zhihu.com/question/26526858
[2]:https://blog.csdn.net/weixin_43314519/article/details/106996639
[3]:https://blog.csdn.net/qq_29591261/article/details/77945561
[4]: 《统计学习方法》（第二版） 李航