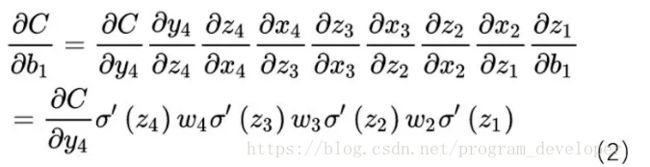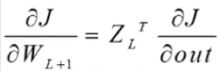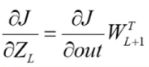CNN，RNN，LSTM，GRU的前后向传播算法（梯度是怎么更新的）

目录

1.简单的梯度计算

2.进阶的梯度计算

3.CNN前向后向算法

4.RNN前向后向算法

5.LSTM前向后向算法

6.GRU前向后向算法

---

为什么要计算梯度？

        直观的讲，我们的网络通过这样的方式进行学习计算，最终输出的结果y为网络根据标签学习来的，网络的第一次前向传播相当于自学，随意学习一种概率分布，但是我们想让预测的结果更加接近“答案”，那我们就需要计算预测与标签之间差距，即loss。然后我们通过降低loss的方式改变权重（更新梯度），缩小预测结果与真实值（标签）之间的差距。

1.简单的梯度计算

先看一个简单的：

以下图的反向传播为例：假设σ为sigmoid，C为代价函数。

下图（1）式为该网络的前向传播公式。

下一个结点的输入为上一个结点输出

根据前向传播公式，我们得出梯度更新公式（这个操作就相当于复合函数求导问题）：

其中由公式（1）得出  ,    

要想求b1的梯度，需要计算前面每一个值的梯度，浅层梯度需要由深层的梯度一步步计算而来。 

上面这个公式看着可能有点蒙，我们根据公式一一来计算：

        上式就相当于对  （其中，，）

求导，要想对x求导，就要先对y求导，要想对y求导，就要先对z求导，上述公式就是这样一步一步得来（上述公式中，x4就相当于y3，x3就相当于y2，即上一层的输出）。 【其实这个例子更直观的求导方式就是直接看公式进行求导，而无需看图】

        上图中值标注了输入值（即）和权重，未标注中间的激活函数，若网络复杂起来，我们就无法根据公式对梯度进行计算，下面，我们看几个更加详细的例子。

2.进阶的梯度计算

该节的梯度求解是从像素级别进行计算的，前面的是从网络层的角度计算的。

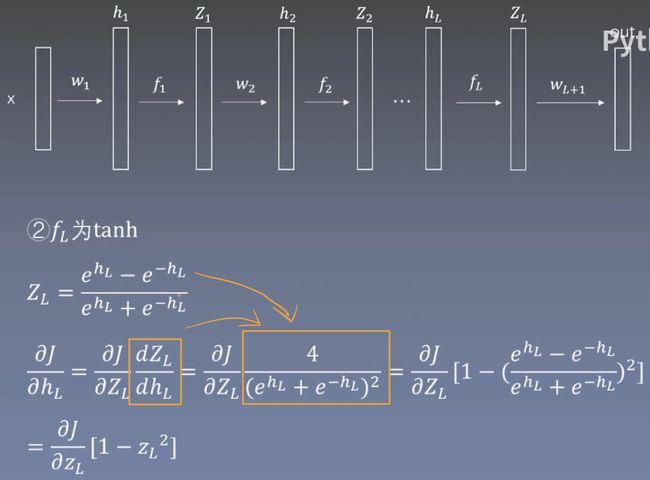
x为输入数据，w为权重，h为隐藏层，f为激活函数，Z为经过激活函数的隐藏层，b为偏置。

下图为一个较小神经网络。

 下图所示为前向传播公式

下面进入反向传播

反向传播时从后向前，一级一级对结点和权重进行梯度更新。

下图为前向传播公式，白色区域的公式由右侧out的公式带入而来，所得为out矩阵的四个值。

此处开始正式计算梯度

对权重W求梯度：

下图左侧为前向公式，右侧为对W求梯度

J是由out与label的差值计算而来，首先需要计算 out 的梯度，即。

首先计算的权重，J先对out求导，已知只有两项含有，故先对中的w求偏导。再一次计算的梯度。

将结果用矩阵的方式表示，如下图所示

注意上面求的 的梯度为W梯度矩阵的元素值

最终得到W矩阵的梯度

我们再回看到上面的网络图，对求梯度的结果等于J对上一层（深层）的梯度左乘下一层（浅层）的结点的转置。

记住这个结论

下面求b的梯度：

同理一次计算b梯度矩阵的每一个值，并将其构成矩阵

最终求得b的梯度为

对结点Z求梯度：

用计算W梯度的方式计算Z梯度矩阵的每个元素值

并写成矩阵的形式

最终得到Z的梯度公式：

所以Z的梯度等于将Z的上一层（深层）的梯度右乘上一层的权重W

下面求隐藏层h的梯度：

        要想求h的梯度，就要先计算Z的梯度，Z的梯度的计算方式我们已经知道了，那要如何计算h的梯度呢？

        我们知道Z是由h经过一个激活函数得来的，公式为

        对h求梯度得到

        将Z的导数带入即可得到当前激活函数下的h的梯度

        不同的激活方式得到不同h梯度

        下面列出了使用sigmoid、tanh和relu激活函数的h梯度

 

 下图中总结了不同层J对权重W、结点Z、偏置b的梯度

 

 总结：如何求最浅层的权重W的梯度

3.CNN前向后向算法

为输入特征图，为输出特征图，卷积核大小为2×2,W和b分别为权重和偏置。

        理论上卷积核在输入特征图x上进行滑动计算，得出y的像素值，但是6×4的矩阵无法与2×2的矩阵直接相乘，那就需要将矩阵进行转换。

        注意，下图上面三个矩阵为理论中卷积的操作，下面三个矩阵为代码底层的计算方式。

        为转换后的矩阵，那这个矩阵是怎么得来的呢？注意观察，卷积核K在x的第一个位置所覆盖的元素为 矩阵的第一行，随着卷积核在x上滑动，每次覆盖的元素值被依次排列到 的矩阵中，如图中橙色方框所示，的行数为输出特征图y的像素数[H-K+1]×[W-K+1] = 5×3 = 15。 

        卷积核被展平为一维列向量。

        这样就可以使与卷积核K进行相乘操作，得到卷积后的结果。

        然后再reshape成5×3大小的特征图。 

        这样就实现了卷积操作

CNN的前后向传播：

CNN的前向传播为

b为一维列向量

损失J对的梯度为

损失J对的梯度为

损失J对的梯度为

我们最终要求x的梯度，但是目前我们求得是的梯度，所以我们就需要计算的梯度

的梯度为

 这个公式怎么理解呢？

我们知道是由卷积在x上滑动得来的，故会有重复的值，所以我们要将中重复的值加起来才是x的梯度。如下图中红色框中所示。

这样就求得了x的梯度。

 以上只是对一张图片进行卷积操作，但实际中，我们是一个batch进行计算的，如果有N个样本做一个batch的训练，梯度应该怎么计算呢？

如图，左边一个batch=3的理论上的卷积操作，右边为底层的卷积操作。

底层的卷积操作，与单张图片类似，输入为三张图片横向拼接，每一张图片的矩阵如橙色点标记所示；多个卷积核也在横向进行拼接；输出结果也相当于多个结果的拼接。

前向后向传播计算方式与单张图片无异。

下图为平均池化的梯度计算，与卷积无异

最大池化的梯度计算

4.RNN前向后向算法

        RNN网络后一个时刻的输入依赖于前一个时刻的输出，这种情况下的前后向传播时怎样进行的呢？

前向传播 ：下图为RNN的前向传播及其公式 

        我们假设有1000ms的语音为“早上好”，每10秒取一个特征，共可以取100个特征（），即t=100，每个特征160维。

        下面我们来看一下每一层的数据流是怎样的。

        x为输入数据，U，V为权重矩阵，b1，b2为偏置，f为激活函数，O为输出。

        t=1：我们假设h1为1000维的矩阵，O为6000维的向量。输入数据x1为右下角橙色所示，160维的行向量，则U为160×1000的向量，b1为1000维的列向量 ，V为1000×6000的矩阵，b2为6000维的列向量，输出的结果O1会经过一个softmax得到预测值（0 or 1）。

        t=2：x2为160的行向量，h2的输入为来自当前层和上一层的输出，其余与上一层一致。

        t=t-1和t时刻的前向传播如下图所示。

权值共享的好处： 减少参数； 可以处理任意长度的序列。

        如果此时有100个特征（t），每个特征（t）都使用一套U，V，W（即权值共享），此时的参数量为P；如果不使用权值共享，则每个时刻的Ut，Vt，Wt都参数都不同，总参数量就会变为原来的100倍，即100P的参数量。

        如果使用权值共享，那任意t时刻都使用同一套U，V，W，如上图左下角所示。如果不使用权值共享，我们在定义网络时就需要定义每一个时刻t的Ut，Vt，Wt，若序列长度增加，及时刻变成了t+i，那多出来的 i 个时刻就没有可分配的U，V，W权重，如此，就无法处理可变长的序列。

后向传播：对结点的更新（反向延时传播，BPtt算法）

        总的损失函数J为每一个特征 t 输出的与i时刻的标签之间的差值的和，下图损失使用的均方差损失。

        J对的梯度：反向传播中，我们需要使用J对每一个结点求导，首先对 进行求导，每个仅与当前损失有关，这样通过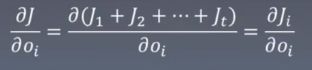就求得了每一个的梯度。

        J对的梯度：已知Si的梯度不仅来自当前层传来的梯度，还来自上一层（深层特征）的产生的梯度。来自当前层的前向传播公式,对求梯度得，和作为输入传递给的前向公式为,对求梯度为,将这两部分的梯度加起来就是的总的梯度。

        J对的梯度：hi相关的前向传播公式为,则J对的梯度为

        J对的梯度：的梯度由同层的 的梯度计算而来，关于的的前向传播公式,由此得出的梯度为。

后向传播：对权重的更新

        此处V,W,U都相对于第 i 个特征层而言        

        对V求梯度：V的梯度由的梯度计算而来，与V相关的前向传播公式为，由此得出V的梯度为。

        对W求梯度：W的梯度由上一层（箭头指向的h）的计算而来，相关的前向传播公式为，得W的梯度为。

        对U求梯度：U的梯度由同层的计算而来，相关的前向传播公式为，故U的梯度为。

        V,W,U的梯度就是将每一个特征（t）的梯度都加起来，可以除一个t算个平均。

        求得的V,W,U用矩阵表示。

        如下图所示。

        V的梯度： 是行向量，，就为一个n行t列的矩阵，n为的维度；为t行m列的矩阵，m为的维度，二者可以相乘，得到一个n行m列的矩阵。

         W的梯度：是一个n行t-1列的矩阵，是一个t-1行m列的矩阵，二者相乘得到一个n行m列的矩阵。

         U的梯度：为行向量，是一个n行t列的矩阵，为t行m列的矩阵，相乘得到一个n行m列的矩阵。

        由于V和U的梯度都需要依赖上一层（深层）的梯度进行计算，从而无法做batch训练，这就是RNN不能并行计算的原因（正向反向都不可以做并行计算）。

 那怎样做才能实现并行训练呢？

不能多样本并行，那就多句话并行。

下面不做详细解释，看图就能理解。

就是将N句话并行处理，拼接为一个矩阵，像这样，，

前向：

后向： 

【求梯度的小技巧（如下图中红色笔记所示）：对结点求梯度为J对上一个结点的梯度右乘上一层权重的转置（若该结点的梯度来自两个方向，即两个箭头，则将这两个所得的梯度相加），对权重求梯度为J对上一个结点的梯度左乘下一个结点的转置。此处的上下以箭头为参考，箭头为上，箭尾为下，而非网络层的上下】

5.LSTM前向后向算法

以下为LSTM的遗忘门，输入门，输出门的前向传播公式。

后向传播：

参数说明：x为输入数据，c为细胞结构，h为隐藏层，m为，y为每一时刻的输出；o，f，i，g分别表示输入数据x作用到遗忘门，输入门，输出门的部分，o，f，i经过sigmoid激活函数，g经过tanh激活函数。

后向传播的计算方式与RNN无异，每个结点和权重的梯度都在图右侧一一列出，可根据图和前向传播公式自行理解。

梯度很好计算，该部分最重要的是：图是由什么公式进行表达的，以及左下角的公式是怎么来的。

图是由上面的前向传播的数据流梳理出来的。黑色线为传到各个门的数据；橙色为细胞结构c的数据，紫色为细胞结构传递到各个门的数据；虚线为经过激活后传递到细胞结构的数据，其中，g只是输入门中的分支流向细胞结构的部分。

公式就是由该图中的数据流走向而来。

        特别注意的是，该前向公式中的结点有f，i，o，m，y，c，权重有W。g是计算c的一个中间步骤（是输入门的一部分），如下图中的前向传播公式中的c，除了来自上一层的从，还有就是i与g的计算，要计算i与g的乘积，先要计算g是什么怎么得来的，就是图中括号的部分。

 

6.GRU前向后向算法

GRU比LSTM更加简易，GRU包含重置门和更新门两个门。

其前向后向传播算法看图即可。