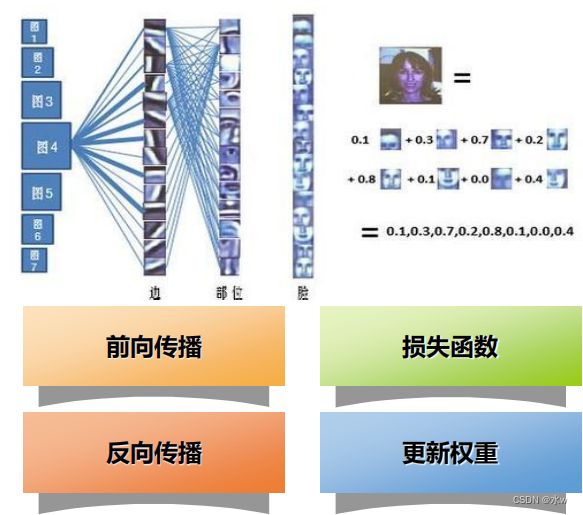
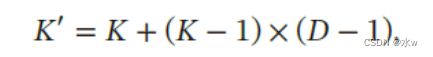深度学习之 10 卷积神经网络3
本文是接着上一篇深度学习之 10 卷积神经网络2_水w的博客-CSDN博客
目录
1 参数学习
设计和学习一个神经网络：
2 回顾：卷积神经网络
3 其他卷积方式
（1）普通卷积
（2）转置卷积
（3）空洞卷积
4 典型网络简介
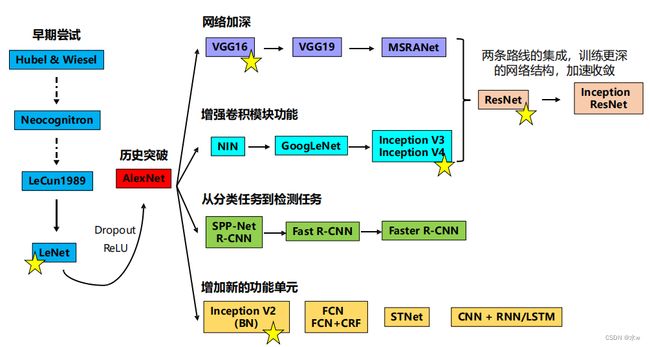
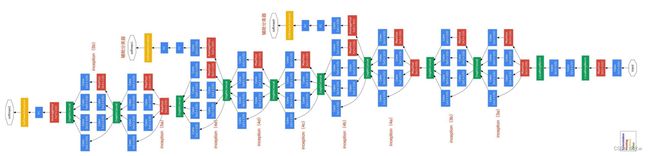
◼ 演化脉络
（1）LeNet 1998
编辑 解释：
（2）AlexNet 2012
（3）Inception网络
Inception module 包含四个分支：
Inception module 优点：
Inception模块 v1：GoogLeNet
Inception模块 v3
（4）残差网络
引入残差学习
为什么是残差?
残差映射
1 参数学习
设计和学习一个神经网络：
Step 1： 设计网络的结构： 卷积层，池化层，全连接层Step 2： 设定超参数 hyper-paramenters卷积层的层数，每个卷积层中卷积核的尺寸、卷积核的个数、卷积操作的步长、 是否padding、训练时的学习率、batch size等如果超参数设置不合理会导致过拟合或者欠拟合！！➢ 超参定义了关于模型的更高层次的概念，如 复杂度 或 学习能力（容量）➢ 超参数是 在开始学习过程之前设置的 ，而 不是通过训练 得到的参数数据➢ 通常情况下， 需要对超参数进行优化 ，选择一组最优超参数，以提高学习的性能和效果。 （通过验证集配置超参数）Step 3： 参数学习 基于大量样本数据，通过误差逆传播算法进行参数学习 （有监督学习）➢ 在卷积神经网络中，主要有两种不同功能的神经层： 卷积层 和池化层➢ 参数为卷积核以及偏置，因此 只需要计算卷积 层中参数的梯度➢ 在全连接前馈神经网络中，梯度主要通过每一层的误差项 进行反向传播，由此可以计算每层参数的梯度➢ 和全连接前馈网络类似，卷积网络也可以通过 误差反向传播算法 来进行参数学习
2 回顾：卷积神经网络
3 其他卷积方式
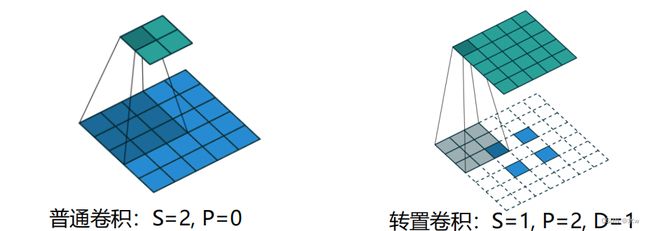
（1）普通卷积
（2）转置卷积
⚫ 一般可通过 卷积操作 来实现 高维特征到低维特征的转换➢ 比如在一维卷积中，一个5维的输入特征，经过一个大小为3 的卷积核，其输出为3维特征➢ 如果设置步长大于1，可以进一步降低输出特征的维数。⚫ 但在一些任务中，我们需要将 低维特征映射到高维特征 ，并且依然希望通过卷积操作来实现 ➢ 转置卷积⚫ 卷积操作其实可以写为仿射变换的形式⚫ 仿射变换（Affine Transformation） 可以实现高维到低维的转换，也可以实现低维到高维的转换：
⚫ 卷积操作也可以写成仿射变换的形式
⚫ 从仿射变换的角度来看两个卷积操作也是形式上的转置关系
⚫ 我们将低维特征映射到高维特征的卷积操作称为 转置卷积 ， 也称为 反卷积（Deconvolution） 。⚫ 在卷积网络中，卷积层的前向计算和反向传播也是一种转置关系。
⚫ 我们可以通过增加卷积操作的步长 >1 来实现对输入特征的下采样操作，大幅降低特征维数⚫ 我们也可以通过减少转置卷积的步长 <1来实现上采样操作，大幅提高特征维数⚫ 步长 <1 的转置卷积 也称为 微步卷积 （Fractionally-Strided Convolution）⚫ 卷积操作的步长为 ，则其对应的转置卷积的步长为 1⚫ 为了实现微步卷积，我们可以 在输入特征之间插入 − 1 个0 来间接地使其移动速度变慢
（3）空洞卷积
Q : 正向传播过程中如何增加输出单元的感受野?① 增加卷积核的大小；② 增加卷积层数；比如两层3 × 3 的卷积可以近似一层5 × 5 卷积的效果；③ 加入池化操作；Q : 这些操作会带来什么问题？① 前两种方式会增加参数数量② 第三种方式会丢失一些信息
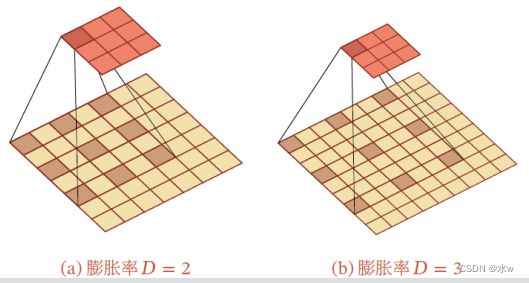
⚫ 空洞卷积 （Atrous Convolution）是一种不增加参数数量，同时增加输出单元感受野的方法⚫ 也称为 膨胀卷积 （ Dilated Convolution ）⚫ 空洞卷积通过给卷积核插入“空洞”来变相地增加其感受野的范围⚫ 如果 在卷积核的每两个元素之间插入 − 1 个空洞 ，卷积核的有效大小为
其中 称为膨胀率（Dilation Rate）。当 = 1 时卷积核为普通的卷积核。
eg：左图中，原有的数据7x7是不变的，把一个3x3的卷积核对应到5x5的区域上，那么我的这个3x3卷积核中 的9个参数，形成这样的间隔式，使得这9个点的数据是有间隔的。----膨胀率
3x3的卷积核的覆盖范围变大，但是9个参数（信息）没变。起到以3x3的卷积核覆盖7x7的区域的作用。
当一个图片里包含的信息没有那么多时， 这种情况下，我们就可以通过空洞卷积来减少参数量，达到相同的效果。
4 典型网络简介
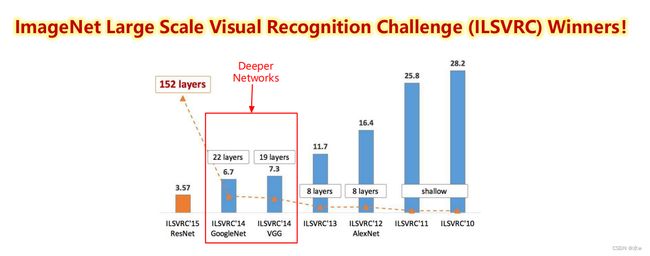
◼ 演化脉络
（1）LeNet 1998
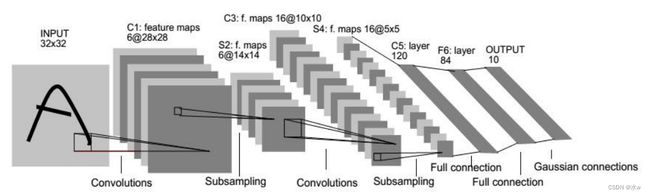
LeNet-5 [LeCun et al., 1998] 虽然提出的时间比较早，但它是一个非常成功的神经网络模型。基于LeNet-5 的手写数字识别系统在20世纪90年代被美国很多银行使用，用来识别支票上面的手写数字。LeNet-5 的网络结构如图所示。最早的深度卷积神经网络模型，用于字符识别。网络具有如下特点：➢ 卷积神经网络使用三个层作为一个系列： 卷积，池化，非线性➢ 使用卷积提取空间特征➢ 使用映射到空间均值的下采样（subsampling）➢ 双曲线（tanh）或S型（sigmoid）形式的非线性激活➢ 多层神经网络（MLP）作为最后的分类器LeNet提供了利用卷积层堆叠进行特征提取的框架，开启了深度卷积神经网络的发展。
解释：
1、输入图像是32x32的大小，第一个卷积层的卷积核的大小是5x5，使用6个卷积核，不做 padding， 因此C1层的大小是28x28，通道数为6。
2、 S2层是一个下采样层，即池化层。在LeNet-5系统，下采样层比较复杂，由4个点也就是2x2，进行下采样的加权平均为1个点，因为这4个加权系数也需要学习得到，这显然增加了模型的复杂度。
3、 第二个卷积层的卷积核的大小是5x5，还是不做padding， 因此C3层的大小为(14-5+1)=10x10。
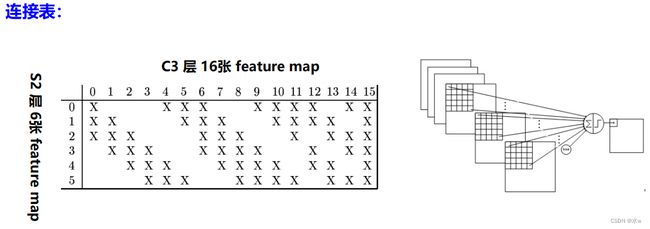
4.、由S2的6通道到C3的16通道，使用 连接表 来进行组合。
（我们通常采用的方式是使用16个卷积核就可以使得S2的6通道变为C3的16通道，那么每个卷积核都要覆盖到原来的所有6个通道，但是此处不是这样做的，它只是覆盖了部分通道。）
简单来说，例如对于C3层第0张特征图，其每一个节点与S2层的第0、1、2共3张特征图的5x5个节点相连接。对于C3层第1张特征图，其每一个节点与S2层的第1、2、3共3张特征图的5x5个节点相连接。
对于C3层第10张特征图，其每一个节点与S2层的第0、1、4、5共4张特征图的5x5个节点相连接。
最后只有一个卷积核覆盖率全部的6个通道。 5、 整个S4层的大小是5x5x16。S4 层是在C3层基础上进行下采样，与S2层类似。
6、 C5层是一个卷积层，有120个特征图。每个单元与S4层的全部16个单元的5*5邻域相连接，故C5特征图的大小为1*1：这构成了S4和C5之间的 全连接 。把原来的立方体的形式拍扁了变成一个向量。得到的C5是一个全连接层。
7、C5层到F6层，把ta从120降到84。
8、然后84再全连接到10，就是以softmax的形式输出10个可能的概率。
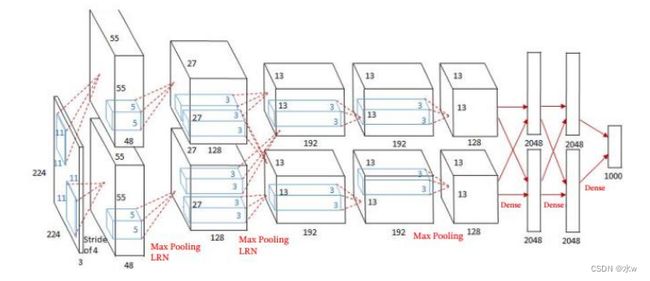
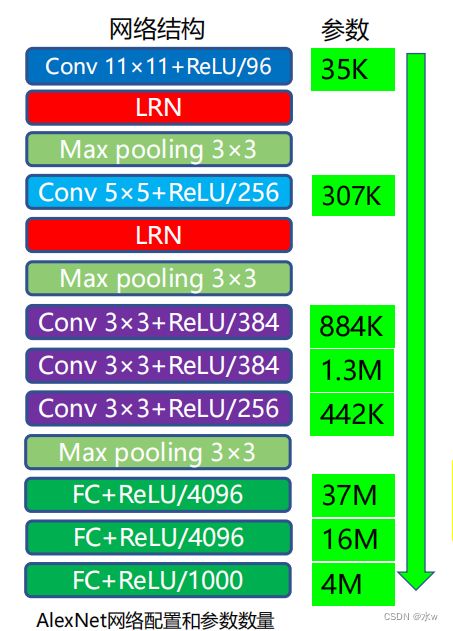
（2）AlexNet 2012
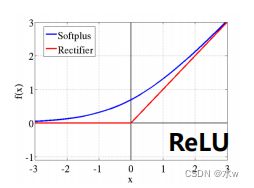
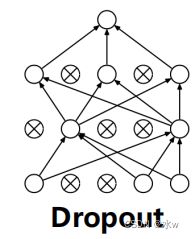
➢ 大数据训练：百万级ImageNet图像数据➢ 防止过拟合：Dropout, 数据增强➢ 分Group实现双GPU并行，局部响应归一化（LRN）层➢ 包括5个卷积层、3个池化层、3个全连接层➢ 非线性激活函数：ReLUAlexNet在LeNet基础上进行了更宽更深的网络设计，首次在CNN中引入了ReLU、Dropout 和Local Response Norm (LRN)等技巧。网络的技术特点如下：➢使用 ReLU（Rectified Linear Units） 作为CNN的激活函数，并验证其效果在较深的网络超过了Sigmoid，成功解决了Sigmoid在网络较深时的梯度消失问题，提高了网络的训练速率。
➢为避免过拟合，训练时使用 Dropout 随机忽略一部分神经元。
➢使用重叠的 最大池化(max pooling) 。最大池化可以避免平均池化的模糊化效果，而采用重叠技巧可以提升特征的丰富性。➢ 提出了LRN（局部响应归一化）层，在ReLU后进行归一化处理，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。➢ 利用 GPU强大的并行计算能力加速网络训练 过程，并采用GPU分块训练的方式解决显存对网络规模的限制。➢ 数据增强 ：利用随机裁剪和翻转镜像操作增加训练数据量，降低过拟合。
➢ 卷积核大小递减，依次为11×11、5×5和3×3。第一层卷积步长为4，之后保持为1。
➢ 在前两层卷积之后分别使用了LRN层。
➢ 与全连接层相比，卷积层包含较少的参数。因此可通过减少全连接层降低网络参数，提高训练时间。
AlexNet在ILSVRC2012图像分类竞赛中将top-5 错误率降 至16.4%，掀起了深度卷积神经网络在各个领域的研究热潮。
（3）Inception网络
2014 ILSVRC winner （22层）• 参数： GoogLeNet (4M) vs AlexNet (60M)• 错误率：6.7%• Inception网络是由有多个 Inception模块 和少量的汇聚层堆叠而成。• Inception 网络有多个版本，其中最早的Inception v1 版本就是非常著名的GoogLeNet [Szegedy et al., 2015]。GoogLeNet 不写为GoogleNet，是为了向LeNet 致敬。GoogLeNet 赢得了2014 年ImageNet 图像分类竞赛的冠军。
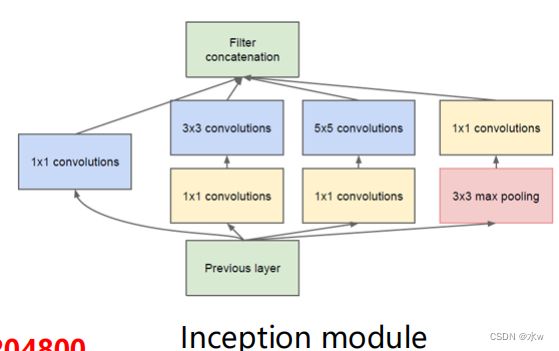
Inception module 包含四个分支：
➢ Shortcut短连接分支：将前一层输入通过1×1卷积，最大的作用就是减少维度数（降维），将原始的数据进行融合；➢ 多尺度滤波分支：输入通过1×1卷积来降维之后分别连接卷积核大小为3和5的卷积；➢ 池化分支：相继连接3×3 pooling和1×1卷积；改变通道数： × × → × × ′
Inception module 优点：
➢ 减少网络参数，降低运算量上一层的输出为100x100x128，经过具有256个通道的5x5卷积层之后(stride=1，pad=2)，输出数据为100x100x256，其中，卷积层的参数为(不考虑偏置)： 128x5x5x256= 819200而假如上一层输出先经过具有32个通道的1x1卷积层，再经过具有256个输出的5x5卷积层，那么输出数据仍为100x100x256，但卷积参数量已经减少大约减少了4倍： 128x1x1x32 + 32x5x5x256= 204800因此，1×1卷积的作用之一是通过降维减少网络开销。➢ 多尺度、多层次滤波➢ 多尺度： 对输入特征图像分别在3×3和5×5的卷积核上滤波，提高了所学特征的多样性，增强了网络对不同尺度的鲁棒性。➢ 多层次： 通过1×1卷积把具有高度相关性的不同通道的滤波结果进行组合，构建出合理的稀疏结构。因此，1×1卷积的另一作用是对低层滤波结果进行有效的组合。
Inception模块 v1：GoogLeNet
GoogLeNet的网络参数为AlexNet的1/12，由9个Inception模块和5个池化层堆叠而成，在ILSVRC 2014 top-5错误率降至6.67%。
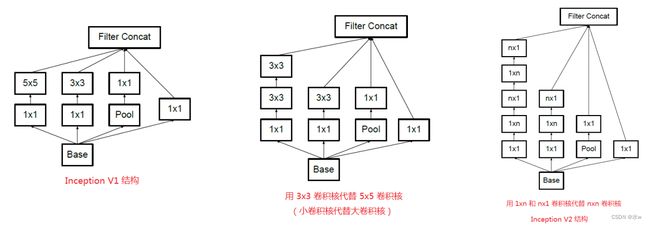
Inception模块 v3
• 用多层的小卷积核来替换大的卷积核，以减少计算量和参数量。
• 使用连续的nx1和1xn来替换nxn的卷积（Inception v2）
• 使用两层3x3的卷积来替换v1中的5x5的卷积
（4）残差网络
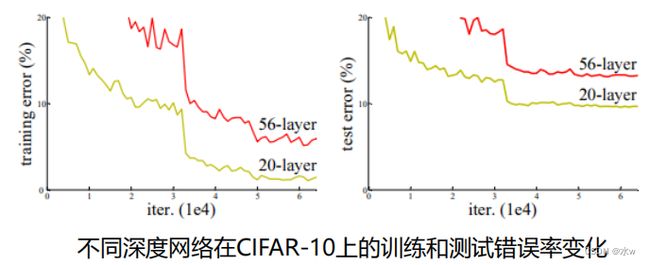
问题：是否可以通过简单的层数堆叠学习更好的网络？➢ 梯度消失和爆炸： 随着网络的加深，在网络中反向传播的梯度会随着连乘变得不稳定，变得特别大或者特别小。 => 通过Normalized initialization 和 Batch normalization得到解决。➢ 网络退化（degradation）: 随着网络的加深，准确率首先达到饱和，然后快速退化。 => 在训练集上的错误率同样增加，因此并非受过拟合的影响。
56层的网络不见得就比20层的网络好，因为50层网络太难训练了。
简单的层数堆叠不能提升网络性能，如何利用网络加深带来的优势？
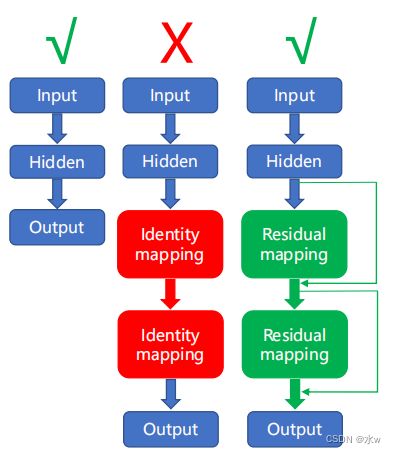
引入残差学习
➢ 实验表明，通过添加 恒等映射 不能提高网络准确率，因此，网络对恒等映射的逼近存在困难。➢ 相比于恒等映射，网络对恒等映射附近扰动的学习更加简单。--> 残差学习
为什么是残差?
✓ 非常深的残差网络能够很容易的优化。
✓ 深度残差网络能够容易地从增加的深度中得到精度收益，同时比先前的网络产生了更好的效果。
残差映射
优点：➢ 没有带来额外的参数和计算开销。➢ 便于和具有相同结构的“平常”网络进行对比。
1）基本的残差映射(相同的维度)：
2）基本的残差映射(不同的维度)：
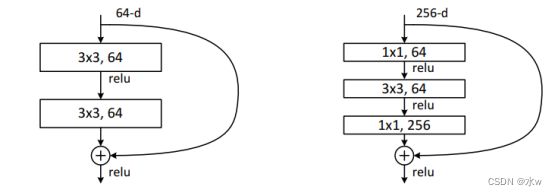
3）更深的残差结构
➢ 用三层连接代替两层(1×1, 3×3, 1×1 卷积)
➢ 1×1：降维和升维
➢ 3×3：具有较小输入输出维度的卷积
➢ 利用深度增加带来的优势，同时减小了网络计算开销。结合了GoogLeNet和ResNet的优点。
更深的残差模块，用于更深的网络结构。左图的浅层模块用于构建ResNet-34，右图的深层模块用于构建ResNet-50/101/152。
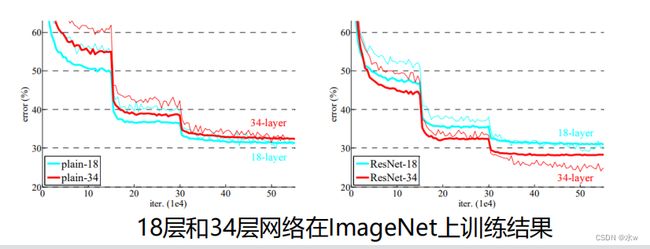
普通的网络，18层比34层的网络要表现好一点。34层的差一些，而且跳动性比较大，不稳定性很高。添加残差之后，34层的网络误差会进一步降低，结果更好一些。
