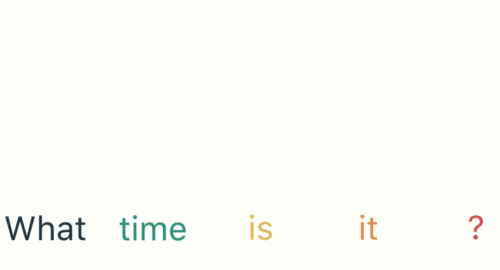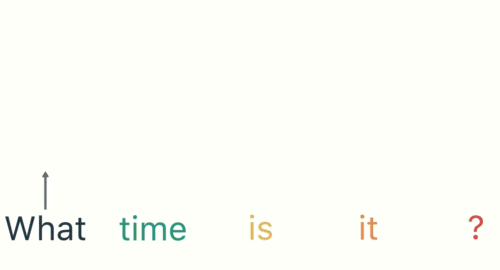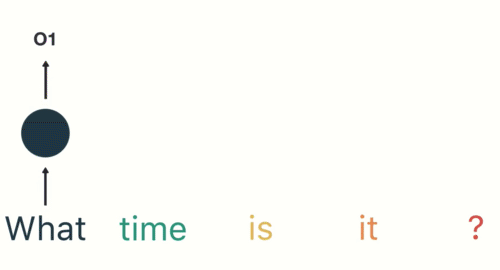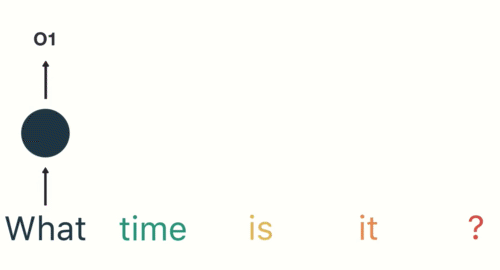深度学习 RNN架构解析
文章目录
- 一、认识RNN模型
-
- 1. 什么是RNN模型
- 2.RNN模型的作用
- 3. RNN模型的分类
- 二、传统RNN模型
-
- 1. 传统RNN的内部结构图
- 2. 内部结构分析
- 3. Pytorch中传统RNN工具的使用
- 4. 输出output和hn的区别
- 5. 优缺点
- 三、LSTM模型
-
- 1. LSTM的内部结构图
- 2. 遗忘门
- 3. 输入门
- 4. 细胞状态
- 5. 输出门
- 6. Bi-LSTM
- 7. Pytorch中LSTM工具的使用:
- 8. 优缺点
- 四、GRU模型
-
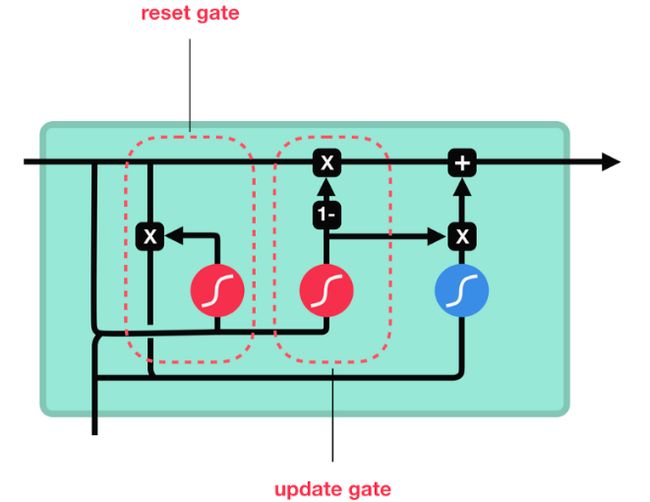
- 1. GRU的内部结构图和计算公式
- 2. Pytorch中GRU工具的使用:
- 3. 优缺点
- 五、注意力机制(简略介绍)
一、认识RNN模型
1. 什么是RNN模型
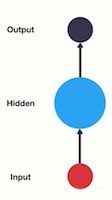
RNN(Recurrent Neural Network), 中文称作循环神经网络, 它一般以序列数据为输入, 通过网络内部的结构设计有效捕捉序列之间的关系特征, 一般也是以序列形式进行输出.
RNN的循环机制使模型隐层上一时间步产生的结果, 能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响.
2.RNN模型的作用
因为RNN结构能够很好利用序列之间的关系, 因此针对自然界具有连续性的输入序列, 如人类的语言, 语音等进行很好的处理, 广泛应用于NLP领域的各项任务, 如文本分类, 情感分析, 意图识别, 机器翻译等.
-
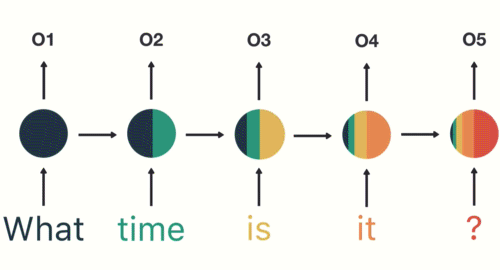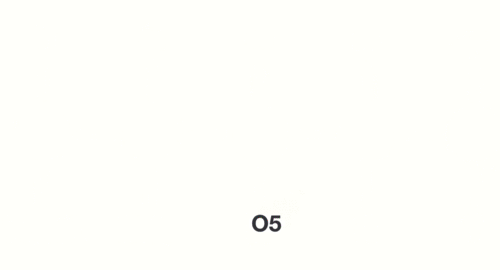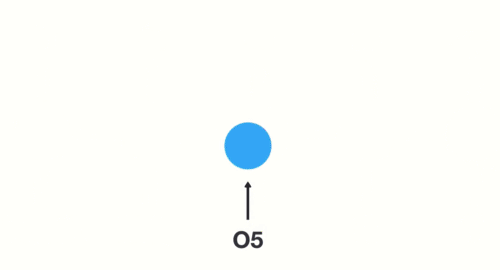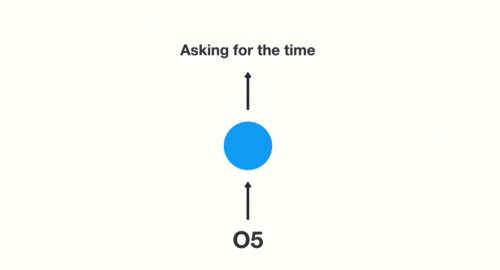
第一步: 用户输入了"What time is it ?", 我们首先需要对它进行基本的分词, 因为RNN是按照顺序工作的, 每次只接收一个单词进行处理.

-
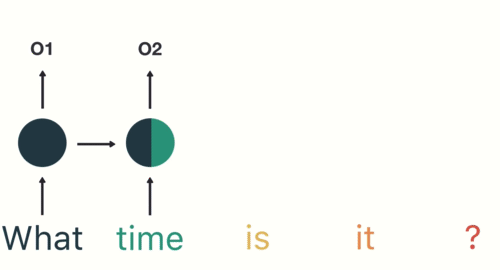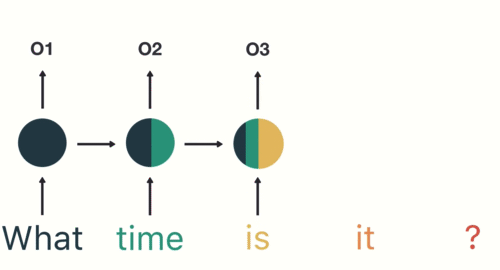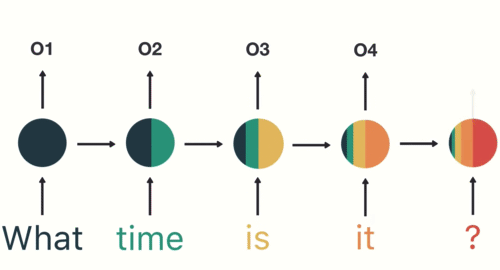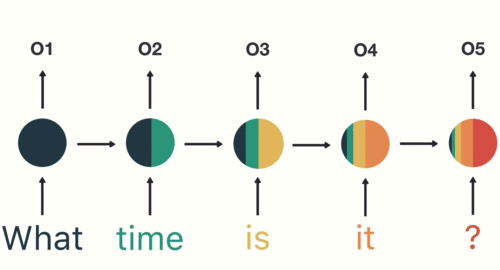
第三步: 继续将单词"time"输送给RNN, 但此时RNN不仅仅利用"time"来产生输出O2, 还会使用来自上一层隐层输出O1作为输入信息.
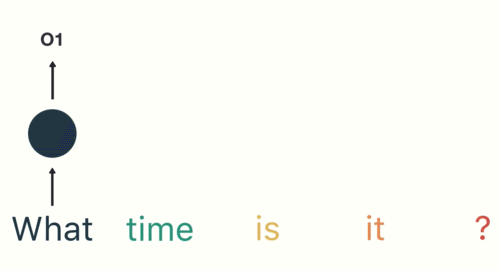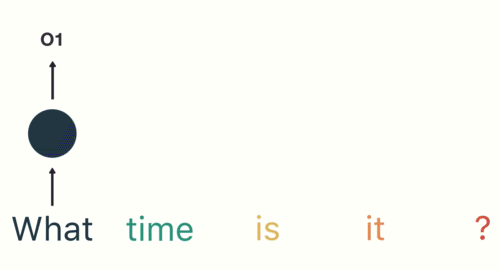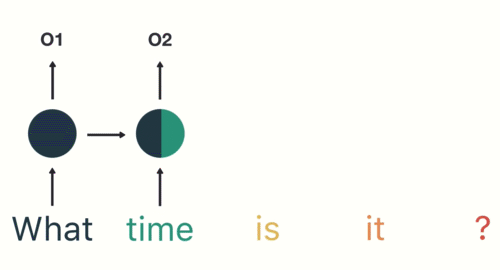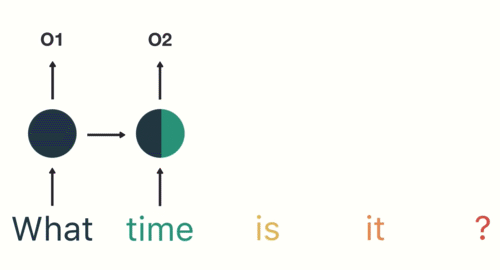
3. RNN模型的分类
这里我们将从两个角度对RNN模型进行分类. 第一个角度是输入和输出的结构, 第二个角度是RNN的内部构造.
-
按照输入和输出的结构进行分类:
- N vs N - RNN
- N vs 1 - RNN
- 1 vs N - RNN
- N vs M - RNN
-
按照RNN的内部构造进行分类:
- 传统RNN
- LSTM
- Bi-LSTM
- GRU
- Bi-GRU
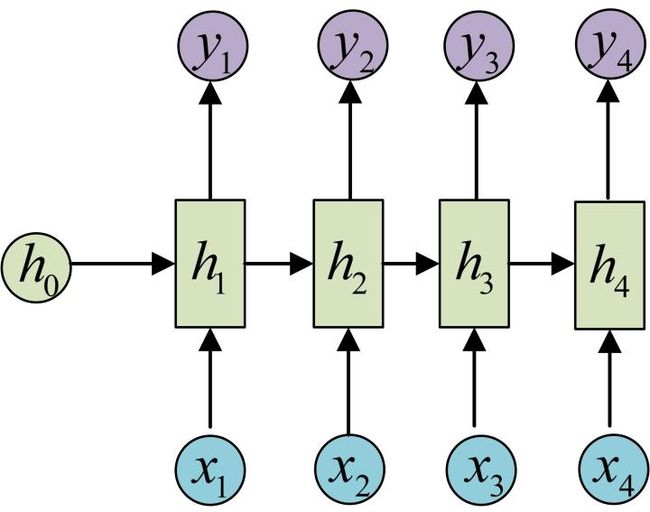
N vs N - RNN:
它是RNN最基础的结构形式, 最大的特点就是: 输入和输出序列是等长的. 由于这个限制的存在, 使其适用范围比较小, 可用于生成等长度的合辙诗句.
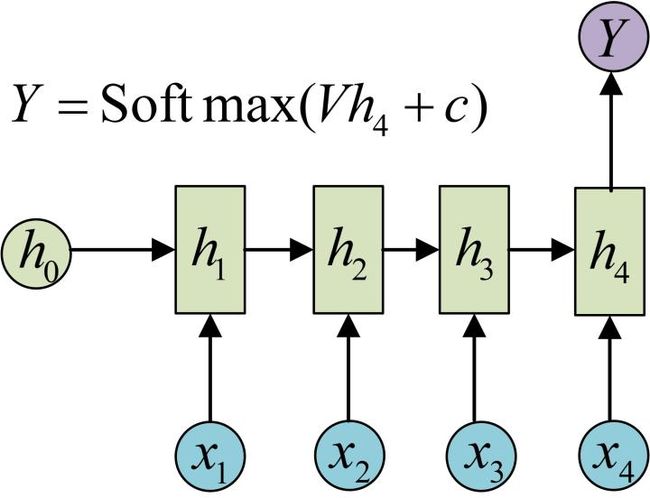
N vs 1 - RNN:
有时候我们要处理的问题输入是一个序列,而要求输出是一个单独的值而不是序列,应该怎样建模呢?我们只要在最后一个隐层输出h上进行线性变换就可以了,大部分情况下,为了更好的明确结果, 还要使用sigmoid或者softmax进行处理. 这种结构经常被应用在文本分类问题上.
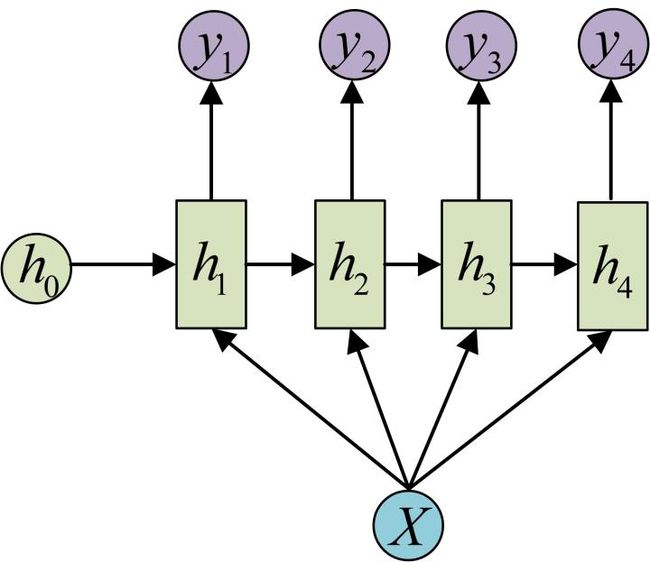
1 vs N - RNN:
如果输入不是序列而输出为序列的情况怎么处理呢?我们最常采用的一种方式就是使该输入作用于每次的输出之上. 这种结构可用于将图片生成文字任务等.
N vs M - RNN:
这是一种不限输入输出长度的RNN结构, 它由编码器和解码器两部分组成, 两者的内部结构都是某类RNN, 它也被称为seq2seq架构. 输入数据首先通过编码器, 最终输出一个隐含变量c, 之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上, 以保证输入信息被有效利用.
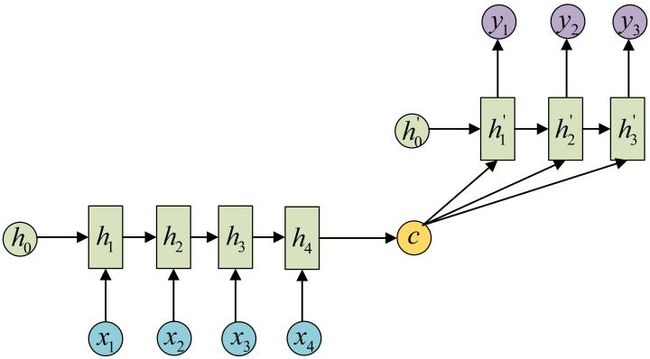
seq2seq架构最早被提出应用于机器翻译, 因为其输入输出不受限制,如今也是应用最广的RNN模型结构. 在机器翻译, 阅读理解, 文本摘要等众多领域都进行了非常多的应用实践.
关于RNN的内部构造进行分类的内容我们将在后面使用单独的小节详细讲解.
二、传统RNN模型
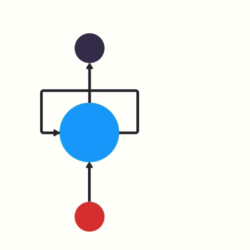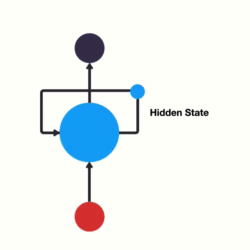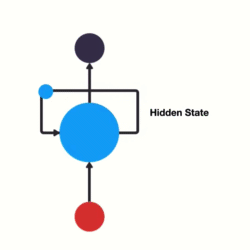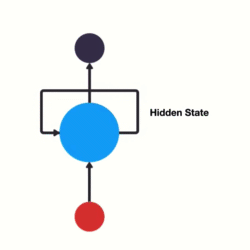
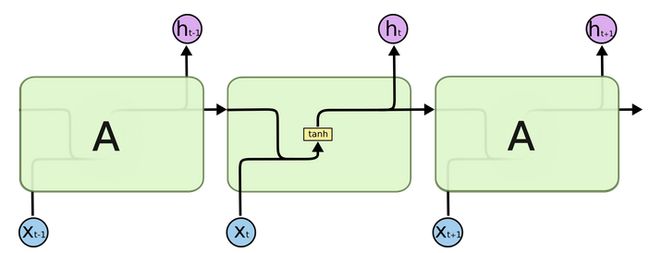
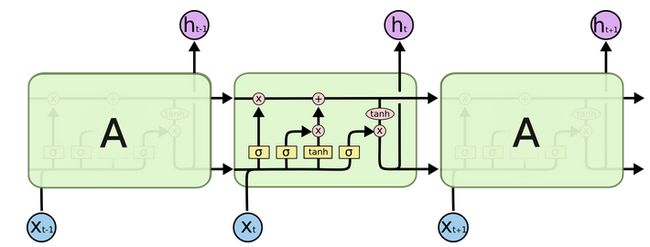
1. 传统RNN的内部结构图
2. 内部结构分析
我们把目光集中在中间的方块部分, 它的输入有两部分, 分别是h(t-1)以及x(t), 代表上一时间步的隐层输出, 以及此时间步的输入, 它们进入RNN结构体后, 会"融合"到一起, 这种融合我们根据结构解释可知, 是将二者进行拼接, 形成新的张量[x(t), h(t-1)], 之后这个新的张量将通过一个全连接层(线性层), 该层使用tanh作为激活函数, 最终得到该时间步的输出h(t), 它将作为下一个时间步的输入和x(t+1)一起进入结构体. 以此类推.
![]()
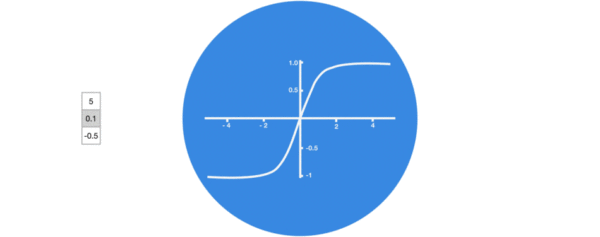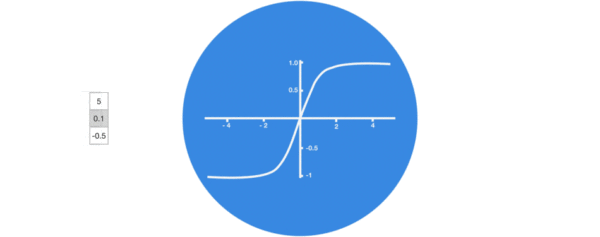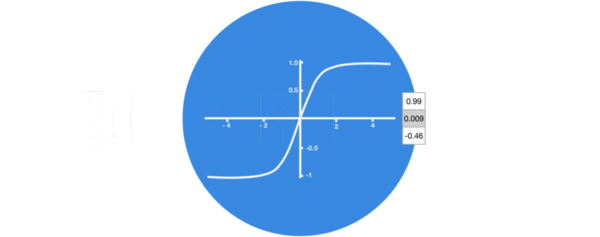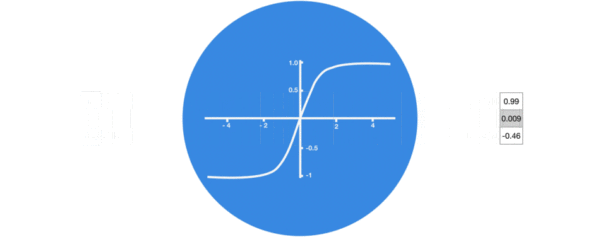
- 激活函数tanh的作用:
用于帮助调节流经网络的值, tanh函数将值压缩在-1和1之间.
3. Pytorch中传统RNN工具的使用
-
位置: 在torch.nn工具包之中, 通过
torch.nn.RNN可调用. -
nn.RNN类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小.
- hidden_size: 隐层张量h中特征维度的大小.
- num_layers: 隐含层的数量.
- nonlinearity: 激活函数的选择, 默认是tanh.
-
nn.RNN类实例化对象主要参数解释:
- input: 输入张量x.
- h0: 初始化的隐层张量h.
nn.RNN使用示例:
# 导入工具包
>>> import torch
>>> import torch.nn as nn
>>> rnn = nn.RNN(5, 6, 1)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(1, 3, 6)
>>> output, hn = rnn(input, h0)
>>> output
tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357, 0.1252],
[ 0.5758, -0.2823, 0.4822, -0.4485, -0.7362, 0.0084],
[ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637, 0.4938]]],
grad_fn=<StackBackward>)
>>> hn
tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357, 0.1252],
[ 0.5758, -0.2823, 0.4822, -0.4485, -0.7362, 0.0084],
[ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637, 0.4938]]],
grad_fn=<StackBackward>)
关于执行过程及更详细解释可参考:https://blog.csdn.net/weixin_41744192/article/details/115270178
4. 输出output和hn的区别
- ouput保存了最后一层所有时间节点(time step)的输出h
- hn保存了每一层最后一个时间节点(time step)的输出h
5. 优缺点
- 传统RNN的优势:
由于内部结构简单, 对计算资源要求低, 相比之后我们要学习的RNN变体:LSTM和GRU模型参数总量少了很多, 在短序列任务上性能和效果都表现优异. - 传统RNN的缺点:
传统RNN在解决长序列之间的关联时, 通过实践,证明经典RNN表现很差, 原因是在进行反向传播的时候, 过长的序列导致梯度的计算异常, 发生梯度消失或爆炸.
- 什么是梯度消失或爆炸呢?
根据反向传播算法和链式法则, 梯度的计算可以简化为以下公式:
![]()
其中sigmoid的导数值域是固定的, 在[0, 0.25]之间, 而一旦公式中的w也小于1, 那么通过这样的公式连乘后, 最终的梯度就会变得非常非常小, 这种现象称作梯度消失. 反之, 如果我们人为的增大w的值, 使其大于1, 那么连乘够就可能造成梯度过大, 称作梯度爆炸.
- 梯度消失或爆炸的危害:
如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败; 梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN值).
三、LSTM模型
LSTM(Long Short-Term Memory)也称长短时记忆结构, 它是传统RNN的变体, 与经典RNN相比能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核心结构可以分为四个部分去解析:
- 遗忘门
- 输入门
- 细胞状态
- 输出门
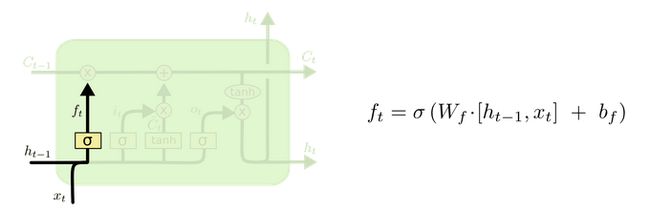
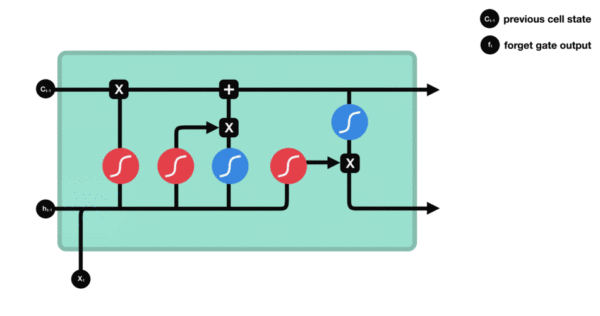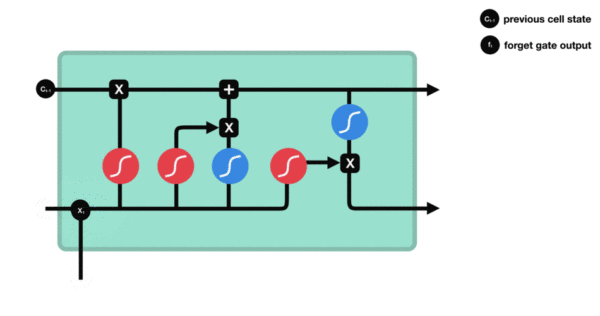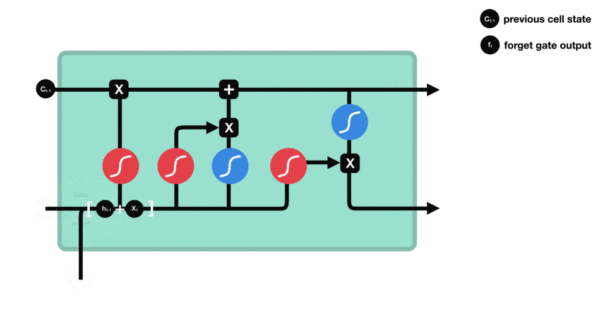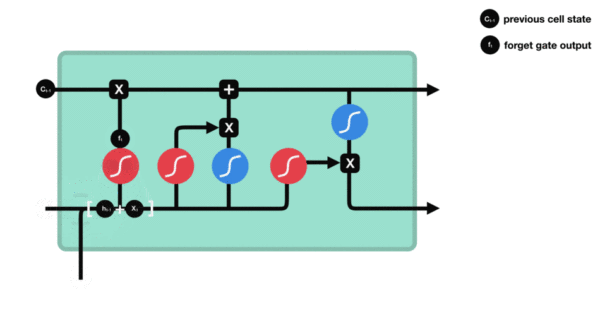
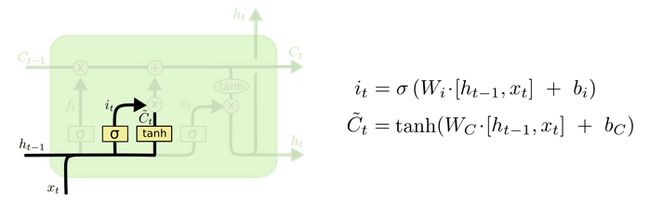
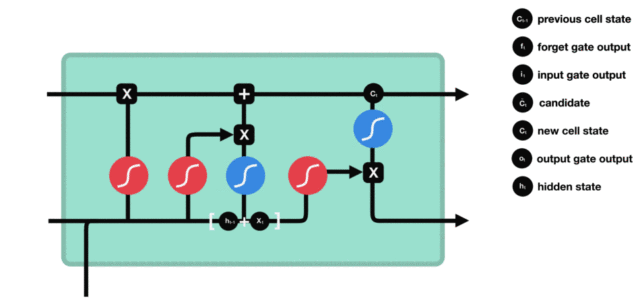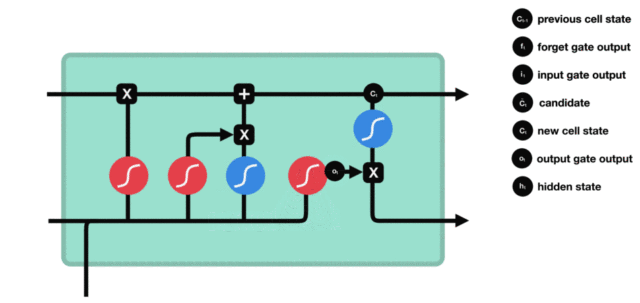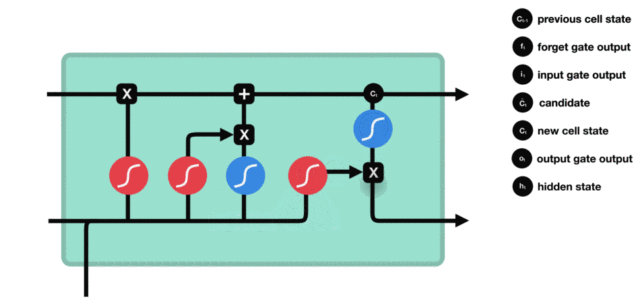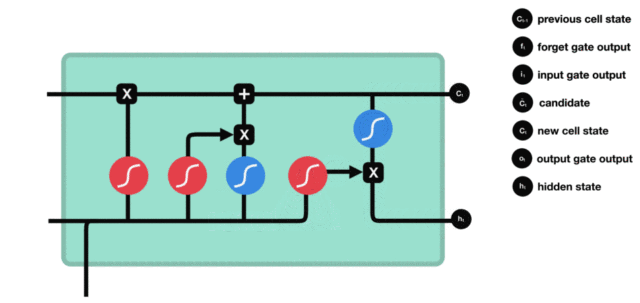
1. LSTM的内部结构图
结构解释图:
2. 遗忘门
-
遗忘门结构分析:
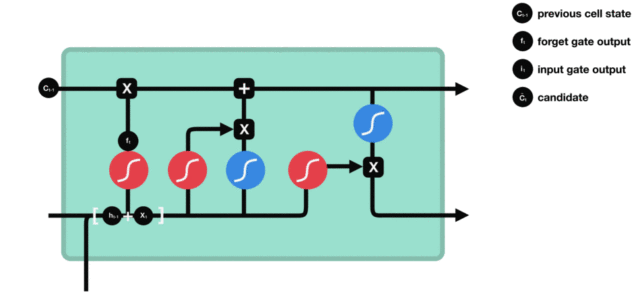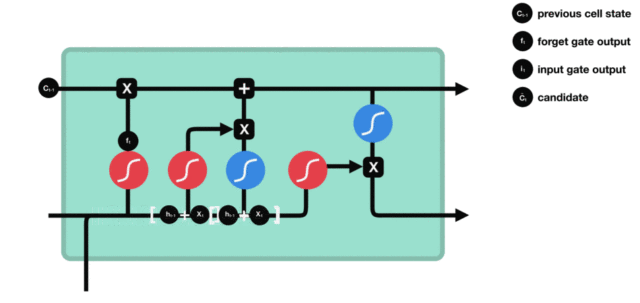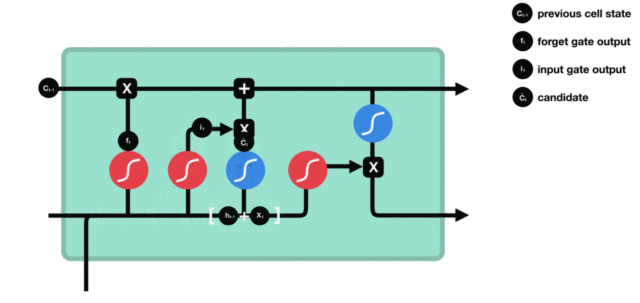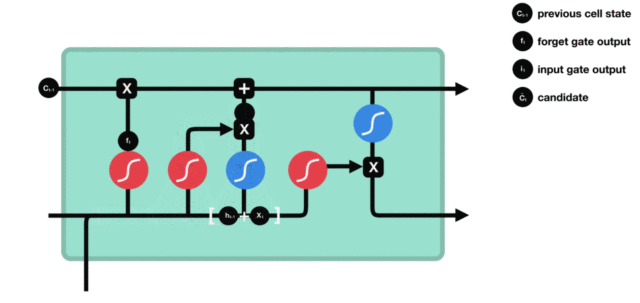
- 与传统RNN的内部结构计算非常相似, 首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接, 得到[x(t), h(t-1)], 然后通过一个全连接层做变换, 最后通过sigmoid函数进行激活得到f(t), 我们可以将f(t)看作是门值, 好比一扇门开合的大小程度, 门值都将作用在通过该扇门的张量, 遗忘门门值将作用的上一层的细胞状态上, 代表遗忘过去的多少信息, 又因为遗忘门门值是由x(t), h(t-1)计算得来的, 因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息.
3. 输入门
-
输入门结构分析:
- 我们看到输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 这个公式意味着输入信息有多少需要进行过滤. 输入门的第二个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.
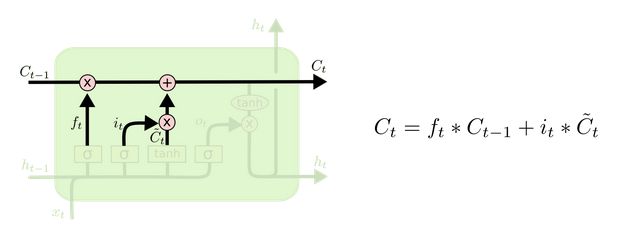
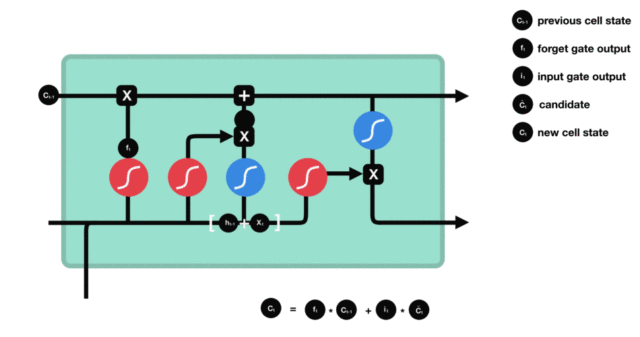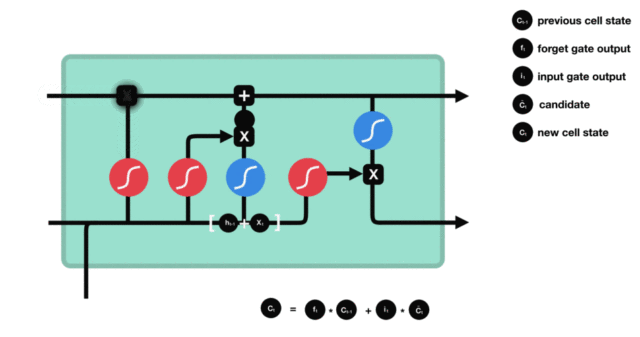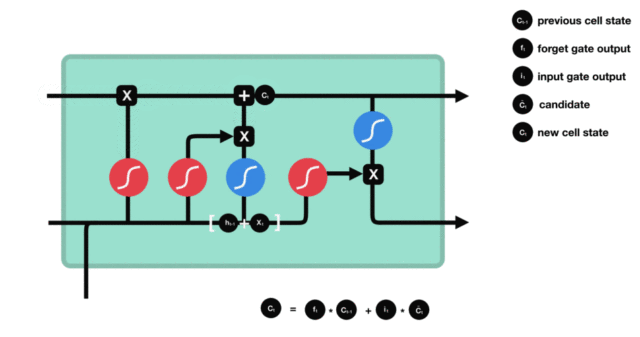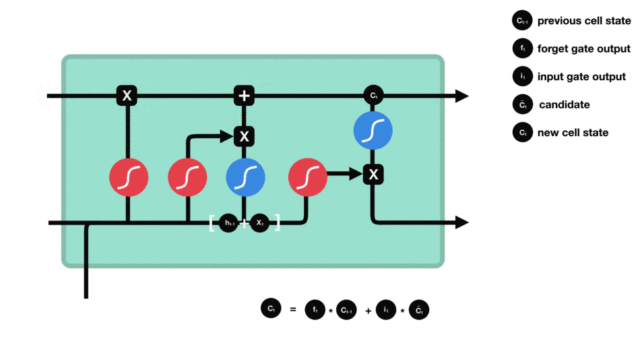
4. 细胞状态
-
细胞状态更新分析:
- 细胞更新的结构与计算公式非常容易理解, 这里没有全连接层, 只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘, 再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果. 最终得到更新后的C(t)作为下一个时间步输入的一部分. 整个细胞状态更新过程就是对遗忘门和输入门的应用.
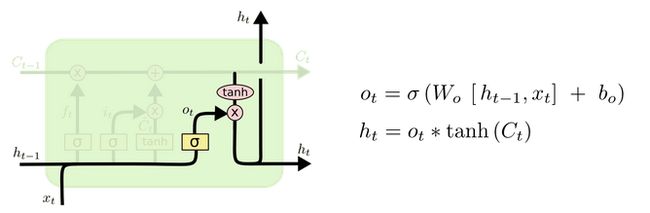
5. 输出门
-
输出门结构分析:
- 输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门,输入门计算方式相同. 第二个即是使用这个门值产生隐含状态h(t), 他将作用在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态h(t).
6. Bi-LSTM
- 什么是Bi-LSTM ?
Bi-LSTM即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出.
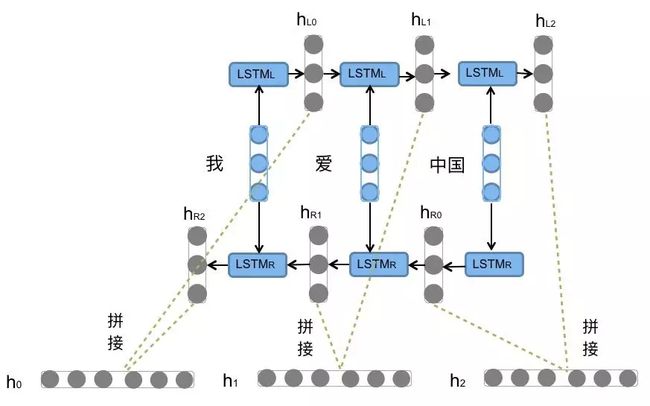
- Bi-LSTM结构分析:
我们看到图中对"我爱中国"这句话或者叫这个输入序列, 进行了从左到右和从右到左两次LSTM处理, 将得到的结果张量进行了拼接作为最终输出. 这种结构能够捕捉语言语法中一些特定的前置或后置特征, 增强语义关联,但是模型参数和计算复杂度也随之增加了一倍, 一般需要对语料和计算资源进行评估后决定是否使用该结构.
7. Pytorch中LSTM工具的使用:
-
位置: 在torch.nn工具包之中, 通过
torch.nn.LSTM可调用. -
nn.LSTM类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小.
- hidden_size: 隐层张量h中特征维度的大小.
- num_layers: 隐含层的数量.
- bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
-
nn.LSTM类实例化对象主要参数解释:
- input: 输入张量x.
- h0: 初始化的隐层张量h.
- c0: 初始化的细胞状态张量c.
nn.LSTM使用示例:
# 定义LSTM的参数含义: (input_size, hidden_size, num_layers)
# 定义输入张量的参数含义: (sequence_length, batch_size, input_size)
# 定义隐藏层初始张量和细胞初始状态张量的参数含义:
# (num_layers * num_directions, batch_size, hidden_size)
>>> import torch.nn as nn
>>> import torch
>>> rnn = nn.LSTM(5, 6, 2)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(2, 3, 6)
>>> c0 = torch.randn(2, 3, 6)
>>> output, (hn, cn) = rnn(input, (h0, c0))
>>> output
tensor([[[ 0.0447, -0.0335, 0.1454, 0.0438, 0.0865, 0.0416],
[ 0.0105, 0.1923, 0.5507, -0.1742, 0.1569, -0.0548],
[-0.1186, 0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
grad_fn=<StackBackward>)
>>> hn
tensor([[[ 0.4647, -0.2364, 0.0645, -0.3996, -0.0500, -0.0152],
[ 0.3852, 0.0704, 0.2103, -0.2524, 0.0243, 0.0477],
[ 0.2571, 0.0608, 0.2322, 0.1815, -0.0513, -0.0291]],
[[ 0.0447, -0.0335, 0.1454, 0.0438, 0.0865, 0.0416],
[ 0.0105, 0.1923, 0.5507, -0.1742, 0.1569, -0.0548],
[-0.1186, 0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
grad_fn=<StackBackward>)
>>> cn
tensor([[[ 0.8083, -0.5500, 0.1009, -0.5806, -0.0668, -0.1161],
[ 0.7438, 0.0957, 0.5509, -0.7725, 0.0824, 0.0626],
[ 0.3131, 0.0920, 0.8359, 0.9187, -0.4826, -0.0717]],
[[ 0.1240, -0.0526, 0.3035, 0.1099, 0.5915, 0.0828],
[ 0.0203, 0.8367, 0.9832, -0.4454, 0.3917, -0.1983],
[-0.2976, 0.7764, -0.0074, -0.1965, -0.1343, -0.6683]]],
grad_fn=<StackBackward>)
关于执行过程及更详细解释可参考:https://blog.csdn.net/weixin_41744192/article/details/115270178
8. 优缺点
- LSTM优势:
LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸, 虽然并不能杜绝这种现象, 但在更长的序列问题上表现优于传统RNN. - LSTM缺点:
由于内部结构相对较复杂, 因此训练效率在同等算力下较传统RNN低很多.
四、GRU模型
GRU(Gated Recurrent Unit)也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:
- 更新门
- 重置门
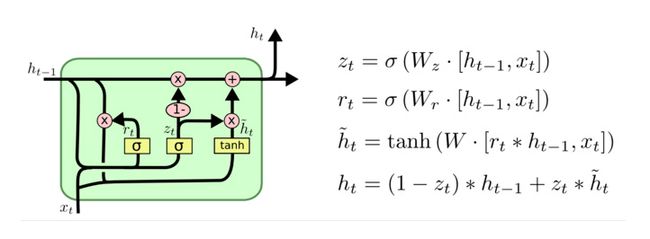
1. GRU的内部结构图和计算公式
结构解释图:
内部结构分析:
和之前分析过的LSTM中的门控一样, 首先计算更新门和重置门的门值, 分别是z(t)和r(t), 计算方法就是使用X(t)与h(t-1)拼接进行线性变换, 再经过sigmoid激活. 之后重置门门值作用在了h(t-1)上, 代表控制上一时间步传来的信息有多少可以被利用. 接着就是使用这个重置后的h(t-1)进行基本的RNN计算, 即与x(t)拼接进行线性变化, 经过tanh激活, 得到新的h(t). 最后更新门的门值会作用在新的h(t),而1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t), 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1).
Bi-GRU与Bi-LSTM的逻辑相同, 都是不改变其内部结构, 而是将模型应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出. 具体参见上小节中的Bi-LSTM.
2. Pytorch中GRU工具的使用:
-
位置: 在torch.nn工具包之中, 通过torch.nn.GRU可调用.
-
nn.GRU类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小.
- hidden_size: 隐层张量h中特征维度的大小.
- num_layers: 隐含层的数量.
- bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
-
nn.GRU类实例化对象主要参数解释:
- input: 输入张量x.
- h0: 初始化的隐层张量h.
nn.GRU使用示例:
>>> import torch
>>> import torch.nn as nn
>>> rnn = nn.GRU(5, 6, 2)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(2, 3, 6)
>>> output, hn = rnn(input, h0)
>>> output
tensor([[[-0.2097, -2.2225, 0.6204, -0.1745, -0.1749, -0.0460],
[-0.3820, 0.0465, -0.4798, 0.6837, -0.7894, 0.5173],
[-0.0184, -0.2758, 1.2482, 0.5514, -0.9165, -0.6667]]],
grad_fn=<StackBackward>)
>>> hn
tensor([[[ 0.6578, -0.4226, -0.2129, -0.3785, 0.5070, 0.4338],
[-0.5072, 0.5948, 0.8083, 0.4618, 0.1629, -0.1591],
[ 0.2430, -0.4981, 0.3846, -0.4252, 0.7191, 0.5420]],
[[-0.2097, -2.2225, 0.6204, -0.1745, -0.1749, -0.0460],
[-0.3820, 0.0465, -0.4798, 0.6837, -0.7894, 0.5173],
[-0.0184, -0.2758, 1.2482, 0.5514, -0.9165, -0.6667]]],
grad_fn=<StackBackward>)
3. 优缺点
- GRU的优势:
GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小. - GRU的缺点:
GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.
五、注意力机制(简略介绍)
可参考:
- 邱锡鹏《神经网络与深度学习》
- https://blog.csdn.net/sophicchen/article/details/107907624
-
什么是注意力:
我们观察事物时,之所以能够快速判断一种事物(当然允许判断是错误的), 是因为我们大脑能够很快把注意力放在事物最具有辨识度的部分从而作出判断,而并非是从头到尾的观察一遍事物后,才能有判断结果. 正是基于这样的理论,就产生了注意力机制. -
什么是注意力计算规则:
它需要三个指定的输入Q(query), K(key), V(value), 然后通过计算公式得到注意力的结果, 这个结果代表query在key和value作用下的注意力表示. 当输入的Q=K=V时, 称作自注意力计算规则. -
常见的注意力计算规则:
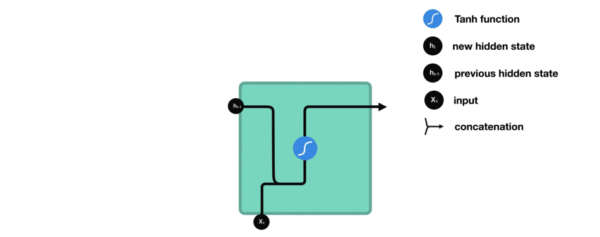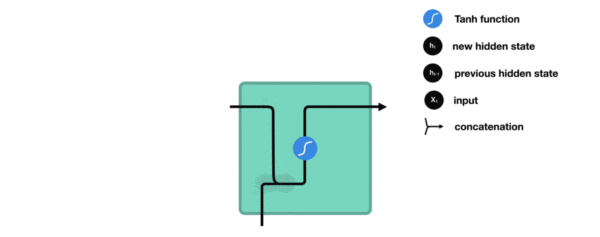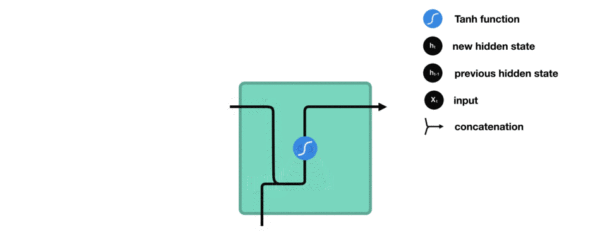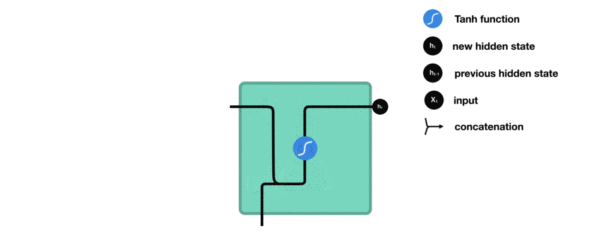
将Q,K进行纵轴拼接, 做一次线性变化, 再使用softmax处理获得结果最后与V做张量乘法.
avatar![]()
将Q,K进行纵轴拼接, 做一次线性变化后再使用tanh函数激活, 然后再进行内部求和, 最后使用softmax处理获得结果再与V做张量乘法.
![]()
将Q与K的转置做点积运算, 然后除以一个缩放系数, 再使用softmax处理获得结果最后与V做张量乘法.
![]()
说明:当注意力权重矩阵和V都是三维张量且第一维代表为batch条数时, 则做bmm运算.bmm是一种特殊的张量乘法运算.
- bmm运算演示:
# 如果参数1形状是(b × n × m), 参数2形状是(b × m × p), 则输出为(b × n × p)
>>> input = torch.randn(10, 3, 4)
>>> mat2 = torch.randn(10, 4, 5)
>>> res = torch.bmm(input, mat2)
>>> res.size()
torch.Size([10, 3, 5])
- 什么是注意力机制
注意力机制是注意力计算规则能够应用的深度学习网络的载体, 同时包括一些必要的全连接层以及相关张量处理, 使其与应用网络融为一体. 使用自注意力计算规则的注意力机制称为自注意力机制.
说明: NLP领域中, 当前的注意力机制大多数应用于seq2seq架构, 即编码器和解码器模型.
-
注意力机制的作用
- 在解码器端的注意力机制: 能够根据模型目标有效的聚焦编码器的输出结果, 当其作为解码器的输入时提升效果. 改善以往编码器输出是单一定长张量, 无法存储过多信息的情况.
- 在编码器端的注意力机制: 主要解决表征问题, 相当于特征提取过程, 得到输入的注意力表示. 一般使用自注意力(self-attention).
-
注意力机制实现步骤
- 第一步: 根据注意力计算规则, 对Q,K,V进行相应的计算.
- 第二步: 根据第一步采用的计算方法, 如果是拼接方法,则需要将Q与第二步的计算结果再进行拼接, 如果是转置点积, 一般是自注意力, Q与V相同, 则不需要进行与Q的拼接.
- 第三步: 最后为了使整个attention机制按照指定尺寸输出, 使用线性层作用在第二步的结果上做一个线性变换, 得到最终对Q的注意力表示.
常见注意力机制的代码分析:
import torch
import torch.nn as nn
import torch.nn.functional as F
class Attn(nn.Module):
def __init__(self, query_size, key_size, value_size1, value_size2, output_size):
"""初始化函数中的参数有5个, query_size代表query的最后一维大小
key_size代表key的最后一维大小, value_size1代表value的导数第二维大小,
value = (1, value_size1, value_size2)
value_size2代表value的倒数第一维大小, output_size输出的最后一维大小"""
super(Attn, self).__init__()
# 将以下参数传入类中
self.query_size = query_size
self.key_size = key_size
self.value_size1 = value_size1
self.value_size2 = value_size2
self.output_size = output_size
# 初始化注意力机制实现第一步中需要的线性层.
self.attn = nn.Linear(self.query_size + self.key_size, value_size1)
# 初始化注意力机制实现第三步中需要的线性层.
self.attn_combine = nn.Linear(self.query_size + value_size2, output_size)
def forward(self, Q, K, V):
"""forward函数的输入参数有三个, 分别是Q, K, V, 根据模型训练常识, 输入给Attion机制的
张量一般情况都是三维张量, 因此这里也假设Q, K, V都是三维张量"""
# 第一步, 按照计算规则进行计算,
# 我们采用常见的第一种计算规则
# 将Q,K进行纵轴拼接, 做一次线性变化, 最后使用softmax处理获得结果
attn_weights = F.softmax(
self.attn(torch.cat((Q[0], K[0]), 1)), dim=1)
# 然后进行第一步的后半部分, 将得到的权重矩阵与V做矩阵乘法计算,
# 当二者都是三维张量且第一维代表为batch条数时, 则做bmm运算
attn_applied = torch.bmm(attn_weights.unsqueeze(0), V)
# 之后进行第二步, 通过取[0]是用来降维, 根据第一步采用的计算方法,
# 需要将Q与第一步的计算结果再进行拼接
output = torch.cat((Q[0], attn_applied[0]), 1)
# 最后是第三步, 使用线性层作用在第三步的结果上做一个线性变换并扩展维度,得到输出
# 因为要保证输出也是三维张量, 因此使用unsqueeze(0)扩展维度
output = self.attn_combine(output).unsqueeze(0)
return output, attn_weights
调用:
query_size = 32
key_size = 32
value_size1 = 32
value_size2 = 64
output_size = 64
attn = Attn(query_size, key_size, value_size1, value_size2, output_size)
Q = torch.randn(1,1,32)
K = torch.randn(1,1,32)
V = torch.randn(1,32,64)
out = attn(Q, K ,V)
print(out[0])
print(out[1])
输出效果:
tensor([[[ 0.4477, -0.0500, -0.2277, -0.3168, -0.4096, -0.5982, 0.1548,
-0.0771, -0.0951, 0.1833, 0.3128, 0.1260, 0.4420, 0.0495,
-0.7774, -0.0995, 0.2629, 0.4957, 1.0922, 0.1428, 0.3024,
-0.2646, -0.0265, 0.0632, 0.3951, 0.1583, 0.1130, 0.5500,
-0.1887, -0.2816, -0.3800, -0.5741, 0.1342, 0.0244, -0.2217,
0.1544, 0.1865, -0.2019, 0.4090, -0.4762, 0.3677, -0.2553,
-0.5199, 0.2290, -0.4407, 0.0663, -0.0182, -0.2168, 0.0913,
-0.2340, 0.1924, -0.3687, 0.1508, 0.3618, -0.0113, 0.2864,
-0.1929, -0.6821, 0.0951, 0.1335, 0.3560, -0.3215, 0.6461,
0.1532]]], grad_fn=<UnsqueezeBackward0>)
tensor([[0.0395, 0.0342, 0.0200, 0.0471, 0.0177, 0.0209, 0.0244, 0.0465, 0.0346,
0.0378, 0.0282, 0.0214, 0.0135, 0.0419, 0.0926, 0.0123, 0.0177, 0.0187,
0.0166, 0.0225, 0.0234, 0.0284, 0.0151, 0.0239, 0.0132, 0.0439, 0.0507,
0.0419, 0.0352, 0.0392, 0.0546, 0.0224]], grad_fn=<SoftmaxBackward>)