【学习机器学习】实验——神经网络
matlab实现神经网络
-
-
- 前言
- 一、实验目的
- 二、实验内容
-
- 1、导入数据
- 2、划分训练集与测试集
- 3、构建神经网络
-
- 3.1 函数参数分析
- 3.2 输入、输出矩阵
- 3.3 调用newff()
- 4、BP训练算法
- 5、网络仿真
- 三、实验结果
- 四、拓展实验
- 五、实验总结
-
前言
越难的理论往往有着最简单的实践,因为老师也知道我们的水平真要写至少也得给一个月时间,所以干脆允许你们使用内建函数了哈。神经网络就是最典型的例子,三个函数,正确调用即可,代码实在没什么可写的所以我把函数的参数意义比较完整的写了出来。代码的部分参考了这篇博客
一、实验目的
-
实现神经网络算法编程
-
采用提供的几个函数(newff()建立模型;train()BP训练;sim()网络仿真)编写代码训练一个单隐层的神经网络。
二、实验内容
1、导入数据
按照惯例,本次实验我选择调用matlab自带的fisheriris数据集。
load fisheriris;
types=tag2num(species);
iris=[meas,types];
2、划分训练集与测试集
考虑到我们需要比较大量的数据做多次训练,因此这次就不采用K折交叉验证来划分数据集了。我们通过随机生成下标,来随机的获取训练集和测试集,具体操作如下:
% 划分数据集。这里通过随机选取下标来划分训练集与测试集
train_index=randsample(150,120,false);
test_index=randsample(150,30,false);
trainData1=iris(train_index,:);
testData1=iris(test_index,:);
save('trainData1.txt','trainData1','-ascii'); % 将其保存至文件是为了更容易划分特征值
save('testData1.txt','testData1','-ascii');
3、构建神经网络
3.1 函数参数分析
我们先分析一下newff()函数的参数,方便确定需要哪些变量。
net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF); % 新版定义
P:输入参数矩阵。(RxQ1),其中Q1代表R元的输入向量。其数据意义是矩阵P有Q1列,每一列都是一个样本,而每个样本有R个属性(特征)。一般矩阵P需要归一化,即P的每一行都归一化到[0 1]或者[-1 1]。
T:目标参数矩阵。(SNxQ2),Q2代表SN元的目标向量。
S:N-1个隐含层的数目(S(i)到S(N-1)),默认为空矩阵[]。输出层的单元数目SN取决于T。返回N层的前馈BP神经网络
TF:相关层的传递函数,默认隐含层为tansig函数,输出层为purelin函数。
BTF:BP神经网络学习训练函数,默认值为trainlm函数。
BLF:权重学习函数,默认值为learngdm。
PF:性能函数,默认值为mse,可选择的还有sse,sae,mae,crossentropy。
IPF:输入处理函数,一般取默认值
OPF:输出处理函数,一般取默认值
DDF:验证数据划分函数,一般取默认值
不过我们不需要那么多的参数设定,所以可以用下面的老版函数:
% newff函数的另一种形式
net=newff(PR,[S1 S2 ... SN],{TF1 TF2 ... TFN},BTF,BLF,PF)
区别就在于,PR:Rx2的矩阵以定义R个输入向量的最小值和最大值。这样我们只需要使用输入矩阵就可以建立模型了,也即:
net = newff(minmax(input),[一层神经元个数,二层神经元个数...],{隐层的传输函数,...,输出层的传输函数},'反向传播的训练函数');
接下来先获取输入与输出矩阵
3.2 输入、输出矩阵
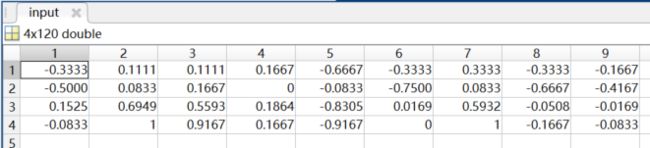
输入矩阵也就是特征值矩阵,iris数据集有4个特征,1个标签,因此我们应该获取一个4行Q1列的input矩阵。下面先从一开始保存的训练集数据中读取每个特征值的数据f1-f4,和标签数据class:
% 读取划分结果,得到四个特征值,与分类标签
[f1,f2,f3,f4,class]=textread('trainData1.txt','%f%f%f%f%f',150);
然后我们用归一化函数,premnmx获得输入矩阵:(注意f1-f4是列向量,需要转置)
% 下面将特征值归一化,保存到输入矩阵input中
[input,minl_train,maxl_train]=premnmx([f1,f2,f3,f4]');
然后是输出矩阵,iris数据集有3个可能的标签值,我们可以用1、2、3来表示,但是这样在计算精度时需要设定阈值,相对比较麻烦。我们用另一种方法来表示输出:
% 构造输出矩阵
s=length(class);
output=zeros(s,3); % 生成s行3列的全零阵
for i=1:s
output(i,class(i))=1; % 第i行,class(i)列为1。表示归为class(i)类
end
可以看到,我构建了一个s行3列的矩阵。每一行数据中,所属标签列为1,其他的为0,这样一来我们计算精度时只需要求预测最大值所在列的下标即可。
3.3 调用newff()
% 调用newff,生成单隐层神经网络
net = newff(minmax(input), [3], {'logsig' }, 'traingdx');
% minmax(input)的作用是确定输入特征的范围,取输入矩阵的最大最小值
% logsig是隐层和输出层使用S形传输函数
% traindx表示使用梯度下降学习法
4、BP训练算法
我们调用train()对神经网络进行训练
net = train(net, input, output');
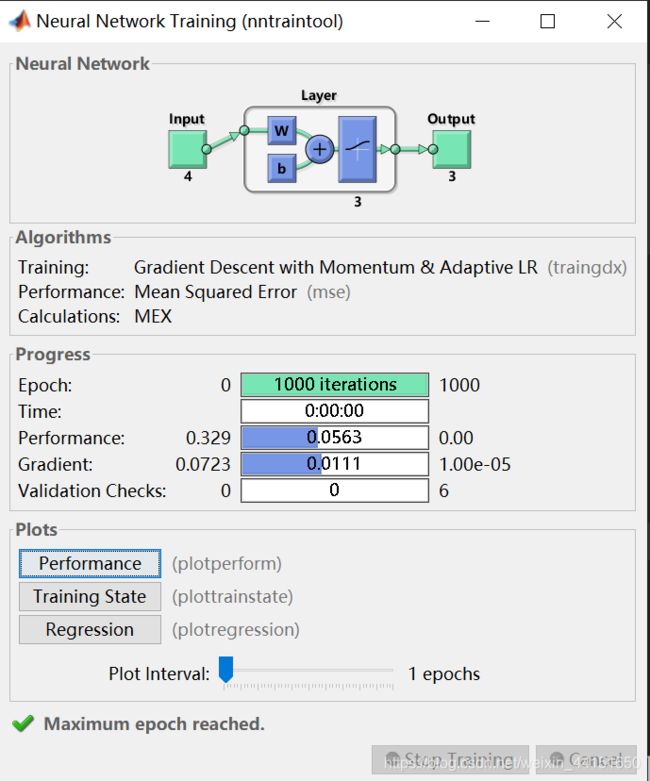
在这个界面中,Neural Network是我们构建的神经网络拓扑图,可以看到本次实验构造的是一个隐层有3个神经元的单隐层神经网路。
Algorithms里面描写了本神经网络的一些算法。Training是训练的算法,上图显示的是自适应动量梯度下降法(也就是traindx)。Performance是性能检测算法,我们使用的是默认的MSE。
Progress进度,描述了训练的过程。Epoch训练次数,最右边的1000是最大训练次数,如果没有特殊情况,训练的次数都会达到最大的训练次数才会停止训练。Time训练时间。Performance,与Algorithms中的算法对应,此处为MSE的最大值。Gradient梯度,进度条中显示的是当前的梯度值,如果梯度值达到最右侧的设定值也会停止训练。Validation Checks校验检查。
Plot,绘图中提供了三种分析图,分别是性能图、训练状态和回归分析。
5、网络仿真
所谓的网络仿真,也就是用测试集检验。我们也需要按照之前获取训练集输入矩阵的步骤,来获取测试集的输入矩阵:
% 读取测试特征值,及ground_truth
[t1,t2,t3,t4,c]=textread('testData1.txt','%f%f%f%f%f',150);
% 测试特征值归一化
[testInput,minl_test,maxl_test]=premnmx([t1,t2,t3,t4]');
之后调用sim()函数,获取预测结果:
% 网络仿真
Y=sim(net,testInput);
三、实验结果
我们对预测结果和真实值进行比较,求一下神经网络的精度:
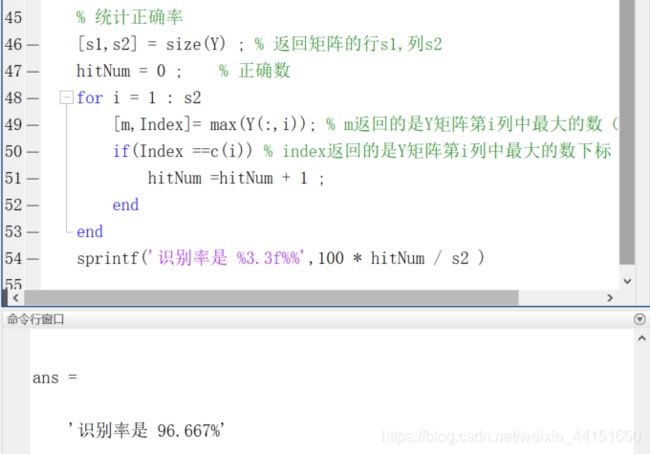
% 统计正确率
[s1,s2] = size(Y) ; % 返回矩阵的行s1,列s2
hitNum = 0 ; % 正确数
for i = 1 : s2
[m,Index]= max(Y(:,i)); % m返回的是Y矩阵第i列中最大的数(归为类)
if(Index ==c(i)) % index返回的是Y矩阵第i列中最大的数下标
hitNum =hitNum + 1 ;
end
end
sprintf('识别率是 %3.3f%%',100 * hitNum / s2 )
四、拓展实验
接下来我们可以尝试使用一些其他的参数设置,看看对神经网络的影响,比如增加隐层,并且在层间使用不同的传递函数:
net = newff(minmax(input),[100 50 10 3] , {'tansig' 'purelin' 'logsig' 'tansig'} , 'traingdx' );
通过对比可以发现,增加隐层后,在Progress部分的Performance得到了明显的提升(MSE值越小越好,这里0.01小于单隐层时的0.05)。不过这对于我们精度的提升是不明显的,因为计算精度后可以看到依旧是90%-100%之间(多次训练可以发现100%的次数提高了,并且下限要高于单隐层时的70%),并且训练时间有明显的增长。因此多层神经网络是否有必要,取决于问题的复杂程度和对精度的要求,iris数据集对于单隐层而言都很简单,没有必要增加隐层去徒增时间。
五、实验总结
本次实验对神经网络从构建、训练、到测试的完整流程进行了实践操作,对于神经网络部分的理论学习进行了补充。