matlab：快速傅里叶（反）变换 FFT&IFFT
文章目录
- 前言
- 一、傅里叶变换的离散性与周期性
- 二、MATLAB 实现快速傅里叶变换 FFT (DFT) 的计算
- 三，FFT 频谱的对称性
- 四，FFT 频谱的频率刻度
- 五，频谱图的绘制（半谱图&全谱图）
- 六 练习 绘制cos信号的频谱图
-
- 半谱图
- 全谱图
- 七，IFFT反傅里叶变换
- 八，采样规则
- 九，二维傅里叶变换
前言
傅里叶变换就是信号的分解过程
即把时域（空域）信号分解成一系列频率下的正弦信号。
傅立叶变换之后的正弦信号每个点都是复数，如a+bi
幅值是：根号下a平方＋b平方
相位是：arctan(b/a)
实部是：a
虚步是：b
幅度和相位结合在一起，就能完全表示傅立叶变换的结果；实部和虚步结合在一起也能完全表示。但是并不是说相位等于虚部。
频谱图：频域和幅值图像&频域和相位图像统称频谱图
◼ 傅里叶变换的好处
✓ 正弦信号比原信号更简单 → 已被充分地研究
✓ 处理正弦信号 → 比处理原信号更简单
✓ 线性系统 → 正弦信号的频率保持性
➢ 输入为正弦信号 → 输出仍是同频率的正弦信号
➢ 幅值和相位可能发生变化 → 但频率与输入信号保持一致
➢ 频率保持性具有很高的工程实用价值
提示：以下是本篇文章正文内容，下面案例可供参考
一、傅里叶变换的离散性与周期性
计算机只能处理有限长度的离散数据序列，所以只有DFS可以通过计算机进行计算
FFT只是加速 DFT 运算的一种快速算法， 在信号理论上没有新的贡献 。其计算的结果和本质内容仍然是离散傅里叶变换 (DFT)
二、MATLAB 实现快速傅里叶变换 FFT (DFT) 的计算
MATLAB 函数的调用格式 → X = fft (x) // X = fft (x, n)
x 是一个时域序列 → 通常为时域信号的采样值
n 用于定义 → 进行 FFT 计算的数据个数
➢ 如果 n 大于 x 的长度 → 自动在 x 的末尾添加 0 → 使得 x 的长度等于 n
➢ 如果 n 小于 x 的长度 → 自动截取 x 中的前 n 个数来进行 FFT 计算
X 返回 FFT 的计算结果 → 通常是一个复数序列
三，FFT 频谱的对称性
从实部和虚部角度分析：
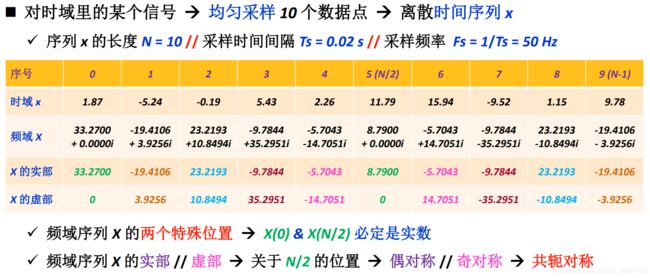
从幅值和相位角度分析
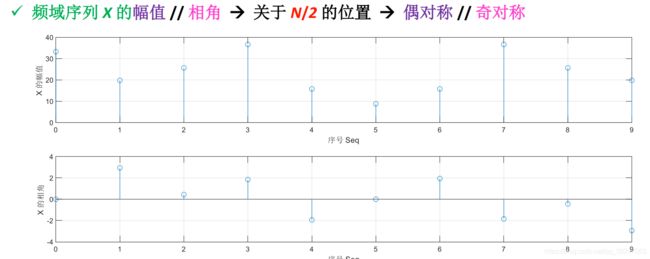
即，两个角度关于N/2都是共轭对称的。
四，FFT 频谱的频率刻度
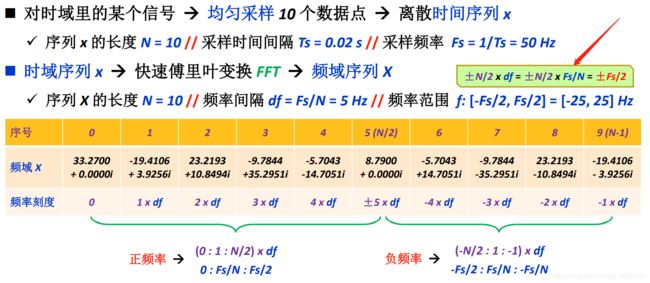
这里解释一下绿框文字。其实是奈奎斯特采样定理（Nyquist sampling theorem），解释了采样率和所测信号频率之间的关系：
采样率Fs必须大于被测信号频率范围的两倍。
另外，有必要解释一下负频率是怎么一回事：
先说结论，所有具有实际物理意义的信号（即实信号，比如f（x）=cos（t））经过傅里叶变换之后的频谱图都是左右对称的（幅频图关于Y轴偶对称，相频图奇对称）。也就是说实信号都是同时有正负频率的，那种只有正频率或负频率的信号（比如f（x）=e^jt）现实中是不存在的，只有数学上的抽象意义。因此无论采样前后，信号都是有负频率的。next，好好的信号为什么会有负频率，该如何理解？下面我们从傅里叶级数的角度理解一下（比较好解释，傅里叶变换大同小异）。傅里叶级数的物理意义很明确：把一个周期信号表示为一系列不同频率的复指数信号的线性组合。上公式：
注意！这个公式的最小组成单位是复指数信号，也就是这个
![[公式]](http://img.e-com-net.com/image/info8/4b8b45aa4d61457b9500d9042f9e5550.jpg){kind=small}
我们知道，复指数信号不是实信号，它在现实中是不存在的，因为它带有虚部j。
那如何用复指数信号合成实信号呢？
答案很简单：只要两个复数共轭就好，实部相加，虚部相抵。也就是欧拉公式:
所以我们在傅里叶级数分析信号的时候，频谱绝对是对称的，用很多对指数相反的复指数信号，就可以合成实信号，也就是说：有k，那必然有-k，否则无法合成实信号。综上，出现负频率的根本原因就是傅里叶级数（变换）的最小单位是复指数信号，如果用傅里叶级数的另一种形式，把信号表示为一系列正余弦信号的组合，就不存在负频率了。
五，频谱图的绘制（半谱图&全谱图）
半谱图（没有负频率）
序列 Y 对应的频率刻度 → (0 : 1 : N/2) x df
→ 0 : Fs/N : Fs/2
全谱图：由于频率刻度正频率在左，负频率在右不符合我们的计算习惯，所以通过ffshift函数进行交换。
针对一维信号， 一般情况下， 更习惯于绘制半谱图
六 练习 绘制cos信号的频谱图
半谱图
clear;clc;close all
%% 定义时域采样信号 x
Fs=100; % 信号采样频率
Ts=1/Fs; % 采样时间间隔
N=200; % 采样信号的长度
t=(0:1:N-1)*Ts; % 定义信号采样的时间点 t
t=t'; % 为了方便查看, 将行向量 t 转置成列向量
f1=16; % 第一个余弦信号的频率
f2=45; % 第二个余弦信号的频率
x=4.5+2.7*cos(2*pi*f1*t+pi/4)+8.2*cos(2*pi*f2*t-pi/6); % 定义时域采样信号 x
%% 对时域采样信号, 执行快速傅里叶变换 FFT
X=fft(x); % 执行 FFT 计算, 结果保存在 X 里
%% 提取 X 里正频率的部分, 并且将 X 里负频率的部分合并到正频率
Y=X(1:N/2+1); % 提取 X 里正频率的部分
Y(2:end-1)=2*Y(2:end-1); % 将 X 里负频率的部分合并到正频率
%% 计算频域序列 Y 的幅值和相角
A=abs(Y); % 计算频域序列 Y 的幅值
Pha=angle(Y); % 计算频域序列 Y 的相角 (弧度制)
R = real(Y); % 计算频域序列 Y 的实部
I = imag(Y); % 计算频域序列 Y 的虚部
%% 定义序列 Y 对应的频率刻度
df=Fs/N; % 频率间隔
f=(0:1:N/2)*df; % 频率刻度
f=f'; % 为了方便查看, 将行向量 f 转置成列向量
%% 绘制时域采样信号 x 的波形
figure
plot(t,x)
xlabel('时间 [s]')
ylabel('信号值 x(t)')
%% 绘制频域序列 Y 的幅频图 & 相频图
figure
subplot(2,1,1)
plot(f,A) % 绘制频域序列 Y 的幅频图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的幅值')
subplot(2,1,2)
plot(f,Pha) % 绘制频域序列 Y 的相频图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的相角')
%% 绘制频域序列 Y 的实部图 & 虚部图
figure
subplot(2,1,1)
plot(f,R) % 绘制频域序列 Y 的实部图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的实部')
subplot(2,1,2)
plot(f,I) % 绘制频域序列 Y 的虚部图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的虚部')
结果如下
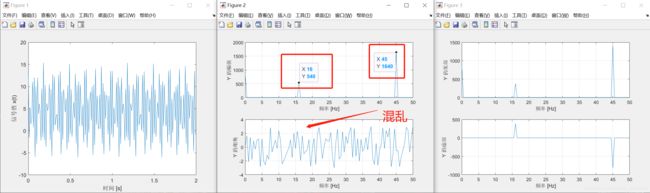
我们发现频率16hz和45hz正好对应，但是幅值过大（540,1640）并且相位混乱。这是因为MATLAB计算误差导致的（fft变换后的虚部大多数极为接近0的小数，我们需要设置一个阈值将这些小数置0来解决相位混乱）。至于幅值只需要/N即可。代码如下
%% 消除相位混乱
X(abs(X)<1e-8)=0; % 将频域序列 X 中, 幅值小于 1e-8 的数值置零
%% 修正频域序列的幅值, 使得 FFT 变换的结果有明确的物理意义
X=X/N; % 将频域序列 X 除以序列的长度 N
最终结果如下：
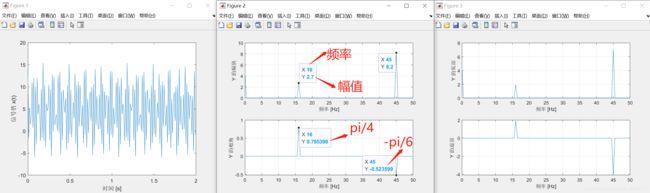
x=4.5+2.7cos(2pif1t+pi/4)+8.2cos(2pif2t-pi/6);
全谱图
%% 定义时域采样信号 x
Fs=100; % 信号采样频率
Ts=1/Fs; % 采样时间间隔
N=200; % 采样信号的长度
t=(0:1:N-1)*Ts; % 定义信号采样的时间点 t
t=t'; % 为了方便查看, 将行向量 t 转置成列向量
f1=16; % 第一个余弦信号的频率
f2=45; % 第二个余弦信号的频率
x=4.5+2.7*cos(2*pi*f1*t+pi/4)+8.2*cos(2*pi*f2*t-pi/6); % 定义时域采样信号 x
%% 对时域采样信号, 执行快速傅里叶变换 FFT
X=fft(x); % 执行 FFT 计算, 结果保存在 X 里
%% 消除相位混乱
X(abs(X)<1e-8)=0; % 将频域序列 X 中, 幅值小于 1e-8 的数值置零
%% 修正频域序列的幅值, 使得 FFT 变换的结果有明确的物理意义
X=X/N; % 将频域序列 X 除以序列的长度 N
%% 将 X 重新排列, 把负频率部分搬移到序列的左边, 把正频率部分搬移到序列的右边
Y=fftshift(X); % 新的频域序列 Y
%% 计算频域序列 Y 的幅值和相角
A=abs(Y); % 计算频域序列 Y 的幅值
Pha=angle(Y); % 计算频域序列 Y 的相角 (弧度制)
R = real(Y); % 计算频域序列 Y 的实部
I = imag(Y); % 计算频域序列 Y 的虚部
%% 定义序列 Y 对应的频率刻度
df=Fs/N; % 频率间隔
f=(-N/2:1:N/2-1)*df; % 频率刻度
f=f'; % 为了方便查看, 将行向量 f 转置成列向量
%% 绘制时域采样信号 x 的波形
figure
plot(t,x)
xlabel('时间 [s]')
ylabel('信号值 x(t)')
%% 绘制频域序列 Y 的幅频图 & 相频图
figure
subplot(2,1,1)
plot(f,A) % 绘制频域序列 Y 的幅频图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的幅值')
subplot(2,1,2)
plot(f,Pha) % 绘制频域序列 Y 的相频图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的相角')
%% 绘制频域序列 Y 的实部图 & 虚部图
figure
subplot(2,1,1)
plot(f,R) % 绘制频域序列 Y 的实部图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的实部')
subplot(2,1,2)
plot(f,I) % 绘制频域序列 Y 的虚部图
grid on
xlabel('频率 [Hz]')
ylabel('Y 的虚部')
七，IFFT反傅里叶变换
我们可以通过ifft函数将频域信号X反变换回原本的空域信号
IX = ifft(X);
%% 绘制频域信号 x 的反傅里叶变换波形
figure
plot(t,IX)
xlabel('时间 [s]')
ylabel('信号值 x(t)')
这里注意，ifft之后结果又从频域的复数变成了空域里的实数，即结果的虚部为0.
八，采样规则
采样频率 Fs // 频率刻度间隔 df = Fs/N
采样定理： 采样频率 Fs ≥ 2Fc（ Fc 为信号里的最高频率成分）
设信号含有 60 Hz 和 72 Hz 两个频率成分 → 采样频率 Fs = 2000 Hz
➢ 时域里采集 N = 100 个数据点 → 频率刻度间隔 df = Fs/N = 20 Hz > (72 – 60 = 12 Hz)
不满足采样定理，此时分不开数据
➢ 时域里采集 N = 500 个数据点 → 频率刻度间隔 df = Fs/N = 4 Hz < (72 – 60 = 12 Hz)
九，二维傅里叶变换
附神贴链接link！！！！！！！！！！！！！！！