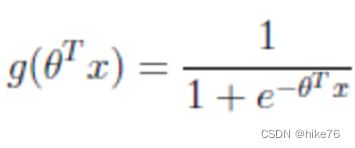机器学习【逻辑回归算法】

一 介绍

逻辑回归（Logistic Regression）是机器学习中的一种分类模型，逻辑回归是一种分类算法，它与回归之间有一定的联系，逻辑回归的输入就是线性回归的输出。由于算法的简单和高效，在实际中应用非常广泛。

1 应用场景

• 广告点击率
• 是否为垃圾邮件
• 是否患病
• 金融诈骗
• 虚假账号

看到上面的例子，可以发现其中的特点，那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器

2 逻辑回归的原理

要想掌握逻辑回归，必须掌握两点：

逻辑回归中，其输入值是什么

如何判断逻辑回归的输出

2.1 输入

逻辑回归的输入就是一个线性回归的结果

2.2 激活函数

sigmoid函数：

判断标准

• 将线性回归的结果输入到sigmoid函数当中
• 输出结果：[0, 1]区间中的一个概率值，默认为0.5为阈值

逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。（方便损失计算）

输出结果解释(重要)：假设有两个类别A，B，并且假设概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.6，那么这个概率值超过0.5，意味着训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别。

之前的线性回归预测结果用均方误差衡量，那如果对于逻辑回归，预测的结果不对该怎么去衡量这个损失呢？有这样一张图

判断思路：使A的预测值靠近1，B的预测值靠近0

3 损失以及优化

3.1 损失

逻辑回归的损失，称之为对数似然损失，公式如下：

分开类别：

怎么理解单个的式子呢？这个要根据log的函数图像来理解

综合完整损失函数

带入上面那个例子计算一遍

3.2 优化

同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于1类别的概率，降低原本是0类别的概率。

二 API介绍

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)
	solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，
		默认: 'liblinear'；用于优化问题的算法。
		对于小数据集来说，“liblinear”是个不错的选择，而“sag”和'saga'对于大型数据集会更快。
		对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
	penalty：正则化的种类
	C：正则化力度

默认将类别数量少的当做正例

LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=" ")，SGDClassifier实现了一个普通的随机梯度下降学习。而使用LogisticRegression(实现了SAG)

三 案例

原始数据的下载地址：https://archive.ics.uci.edu/ml/machine-learning-databases/

数据描述

（1）699条样本，共11列数据，第一列用语检索的id，后9列分别是与肿瘤相关的医学特征，最后一列表示肿瘤类型的数值。

（2）包含16个缺失值，用”?”标出。

1 分析

1.获取数据
2.基本数据处理
2.1 缺失值处理
2.2 确定特征值,目标值
2.3 分割数据
3.特征工程(标准化)
4.机器学习(逻辑回归)
5.模型评估

2 代码

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
# 出现证书安全问题需要加上以下两行代码
import ssl
ssl._create_default_https_context = ssl._create_unverified_context
# 1.获取数据
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin','Normal Nucleoli', 'Mitoses', 'Class']

data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",names=names)
data.head()
# 2.基本数据处理
# 2.1 缺失值处理
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.2 确定特征值,目标值
x = data.iloc[:, 1:10]
x.head()
y = data["Class"]
y.head()
# 2.3 分割数据
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 3.特征工程(标准化)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.机器学习(逻辑回归)
estimator = LogisticRegression()
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 模型基本评估
y_predict = estimator.predict(x_test)
print("预测值是：\n",y_predict)
score= estimator.score(x_test, y_test)
print("准确率是：\n",score)

在很多分类场景当中不一定只关注预测的准确率！

比如以这个癌症举例子，并不关注预测的准确率，而是关注在所有的样本当中，癌症患者有没有被全部预测（检测）出来。

四 分类评估方法

1.分类评估方法

1.1 精确率与召回率

1.1.1 混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

1.1.2 精确率(Precision)与召回率(Recall)

精确率：预测结果为正例样本中真实为正例的比例，也称查准率

准确率 = （TP + TN） / （TP + TN + FP + FN）

精确率 = TP / (TP + FP)

召回率：真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力），也称查全率

召回率 = TP / （TP + FN）

1.2 F1-score

还有其他的评估标准，F1-score，反映了模型的稳健型

1.3 分类评估报告api

sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
	y_true：真实目标值
	y_pred：估计器预测目标值
	labels:指定类别对应的数字
	target_names：目标类别名称
	return：每个类别精确率与召回率

from sklearn.metrics import classification_report
# 5.2 其他评估
ret = classification_report(y_test, y_predict, labels=(2,4), target_names=("良性", "恶性"))
print(ret)

假设这样一个情况，如果99个样本癌症，1个样本非癌症，不管怎样将这100个人全都预测为正例(默认癌症为正例)，准确率就为99%但是这样效果并不好，这就是样本不均衡下的评估问题

那么如何衡量样本不均衡下的评估？

2 ROC曲线与AUC指标

2.1 TPR与FPR

TPR = TP / (TP + FN)

所有真实类别为1的样本中，预测类别为1的比例，正确预测

FPR = FP / (FP + TN)

所有真实类别为0的样本中，预测类别为1的比例，错误预测

2.2 ROC曲线

通过TPR和FPR进行图像绘制，绘制完成之后，形成指标AUC

ROC曲线的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5

2.3 AUC指标

• AUC的概率意义是随机取一对正负样本，正样本得分大于负样本的概率
• AUC的最小值为0.5，最大值为1，取值越高越好
• AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5

最终AUC的范围在[0.5, 1]之间，并且越接近1越好

2.4 AUC计算API

from sklearn.metrics import roc_auc_score
	sklearn.metrics.roc_auc_score(y_true, y_score)
		计算ROC曲线面积，即AUC值
		y_true：每个样本的真实类别，必须为0(反例),1(正例)标记
		y_score：预测得分，可以是正类的估计概率、置信值或者分类器方法的返回值

# 不平衡二分类问题评估方法
# 0.5~1之间，越接近于1约好
y_test = np.where(y_test > 2.5, 1, 0)
print("AUC指标：", roc_auc_score(y_test, y_predict)）

AUC只能用来评价二分类

AUC非常适合评价样本不平衡中的分类器性能

五 ROC曲线的绘制

• 构建模型，把模型的概率值从大到小进行排序

• 从概率最大的开始取值，进行TPR和FPR计算，之后构建整体模型，得到结果

• 本质是在求解积分（面积）

下面是分别构建三个模型，进而得到最终的ROC曲线

关于ROC曲线的绘制过程，通过以下举例进行说明

假设有6次展示记录，有两次被点击了，得到一个展示序列（1:1, 2:0, 3:1, 4:0, 5:0, 6:0），前面的表示序号，后面的表示点击（1）或没有点击（0）。

然后在这6次展示的时候都通过model算出了点击的概率序列。

下面看三种情况

1 曲线绘制

1.1 概率序列1

如果概率的序列是（1:0.9, 2:0.7, 3:0.8, 4:0.6, 5:0.5, 6:0.4）

与原来的序列一起，得到序列（从概率从高到低排）

序号	1	3	2	4	5	6
预测	1	1	0	0	0	0
概率	0.9	0.8	0.7	0.6	0.5	0.4

上表说明：序号1有百分之90概率被点击，序号3有百分之80概率被点击，序号2,4,5,6,分别有百分之70,60,50,40概率没有被点击，现有阈值，高于百分之75被点击，否则没被点击

全部预测正确

绘制的步骤是：

1）把概率序列从高到低排序，得到顺序（1:0.9, 3:0.8, 2:0.7, 4:0.6, 5:0.5, 6:0.4）；

2）从概率最大开始取一个点作为正类，取到点1，计算得到TPR=0.5，FPR=0.0；

上例中正例有2个（1,3），负例有4个（2,4,5,6）

现取到一个点1，共一个点，假设只有1个正例，TP为1（概率大于阈值且真实结果为1），FP为0，因为正例有2个，可以推断出FN为1，TPR = 1 / 2，FPR = 0 / 4

3）从概率最大开始，再取一个点作为正类，取到点3，计算得到TPR=1.0，FPR=0.0；

再取到一个点3，现有2个点，假设有2个正例，TP为2（概率都大于阈值且真实结果为1），FP为0，因为正例有2个，可以推断出FN为0，TPR = 2 / 2，FPR = 0 / 4

4）再从最大开始取一个点作为正类，取到点2，计算得到TPR=1.0，FPR=0.25;

再取到一个点2，现有3个点，假设有3个正例，TP为2，FP为1（有一个预测错了），因为正例有2个，可以推断出FN为0，TPR = 2 / 2，FPR = 1 / 4

5）以此类推，得到6对TPR和FPR。

然后把这6对数据组成6个点(0,0.5),(0,1.0),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)。

这6个点在二维坐标系中能绘出来，就是ROC曲线

1.2 概率序列2

如果概率的序列是（1:0.9, 2:0.8, 3:0.7, 4:0.6, 5:0.5, 6:0.4）

与原来的序列一起，得到序列（从概率从高到低排）

1	0	1	0	0	0
0.9	0.8	0.7	0.6	0.5	0.4

阈值同样为百分之75，有一个预测错了

绘制的步骤是：

1）把概率序列从高到低排序，得到顺序（1:0.9,2:0.8,3:0.7,4:0.6,5:0.5,6:0.4）；

2）从概率最大开始取一个点作为正类，取到点1，计算得到TPR=0.5，FPR=0.0；

3）从概率最大开始，再取一个点作为正类，取到点2，计算得到TPR=0.5，FPR=0.25；

4）再从最大开始取一个点作为正类，取到点3，计算得到TPR=1.0，FPR=0.25;

5）以此类推，得到6对TPR和FPR。

然后把这6对数据组成6个点(0,0.5),(0.25,0.5),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)。

这6个点在二维坐标系中能绘出来，就是ROC曲线

1.3 概率序列3

与原来的序列一起，得到序列（从概率从高到低排）

0	0	0	0	1	1
0.9	0.8	0.7	0.6	0.5	0.4

两个都预测错了

绘制的步骤是：

1）把概率序列从高到低排序，得到顺序（6:0.9,5:0.8,4:0.7,2:0.6,3:0.5,1:0.4）；

2）从概率最大开始取一个点作为正类，取到点6，计算得到TPR=0.0，FPR=0.25；

3）从概率最大开始，再取一个点作为正类，取到点5，计算得到TPR=0.0，FPR=0.5；

4）再从最大开始取一个点作为正类，取到点4，计算得到TPR=0.0，FPR=0.75;

5）以此类推，得到6对TPR和FPR。

然后把这6对数据组成6个点(0.25,0.0),(0.5,0.0),(0.75,0.0),(1.0,0.0),(1.0,0.5),(1.0,1.0)。

这6个点在二维坐标系中能绘出来

2 意义解释

如上图的例子，总共6个点，2个正样本，4个负样本，取一个正样本和一个负样本的情况总共有8种

上面的第一种情况，从上往下取，无论怎么取，正样本的概率总在负样本之上，所以分对的概率为1，AUC=1。再看那个ROC曲线，它的积分也是1，ROC曲线的积分与AUC相等

上面第二种情况，如果取到了样本2和3，那就分错了，其他情况都分对了；所以分对的概率是0.875，AUC=0.875。再看那个ROC曲线，它的积分也是0.875，ROC曲线的积分与AUC相等

上面的第三种情况，无论怎么取，都是分错的，所以分对的概率是0，AUC=0.0。再看ROC曲线，它的积分也是0.0，ROC曲线的积分与AUC相等

其实AUC的意思是——Area Under roc Curve，就是ROC曲线的积分，也是ROC曲线下面的面积

绘制ROC曲线的意义很明显，不断地把可能分错的情况扣除掉，从概率最高往下取的点，每有一个是负样本，就会导致分错排在它下面的所有正样本，所以要把它下面的正样本数扣除掉（1-TPR，剩下的正样本的比例）。总的ROC曲线绘制出来了，AUC就定了，分对的概率也能求出来了