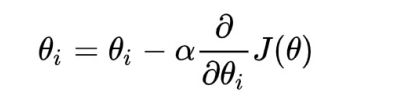机器学习中的线性回归(Python)
写在前面:很久没有更新博客,今年刚考上研究生,现在在校了,有很多时间研究技术了,接下来将会不断的写出更多高质量的文章,希望大家会喜欢,同时欢迎大家能给我提出宝贵意见。
1. 性回归的定义
线性回归:是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
其表达形式为:y = w’x+e,e为误差服从均值为0的正态分布。回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
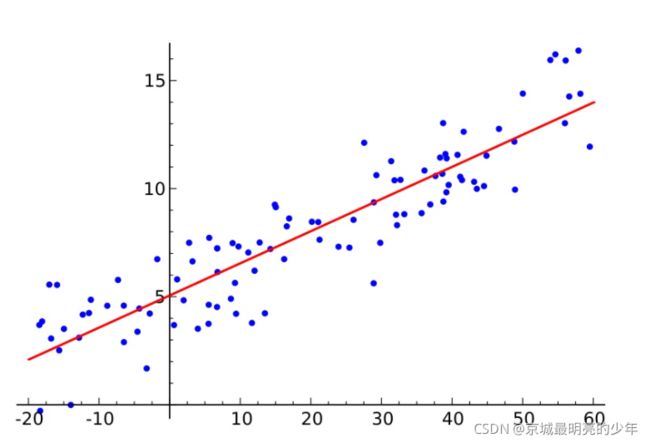
【标哥通俗话】:线性回归的就是在一堆数据里面找到一个规律,也就是一个函数模型,是的能够大概预测里面数据的走向趋势,就像上面的直线表明了一个大概方向。
举例:
最终成绩(y) = 平时成绩(x1)x 0.3 + 期末成绩(x2 ) X 0.7
这个就是最简单的一种线性回归
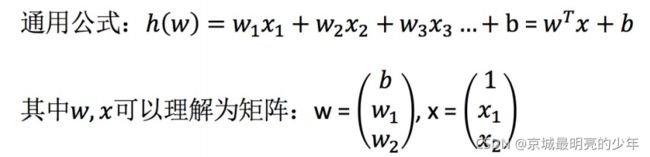
2. 特征与目标
几种回归类别:

单变量的线型回归
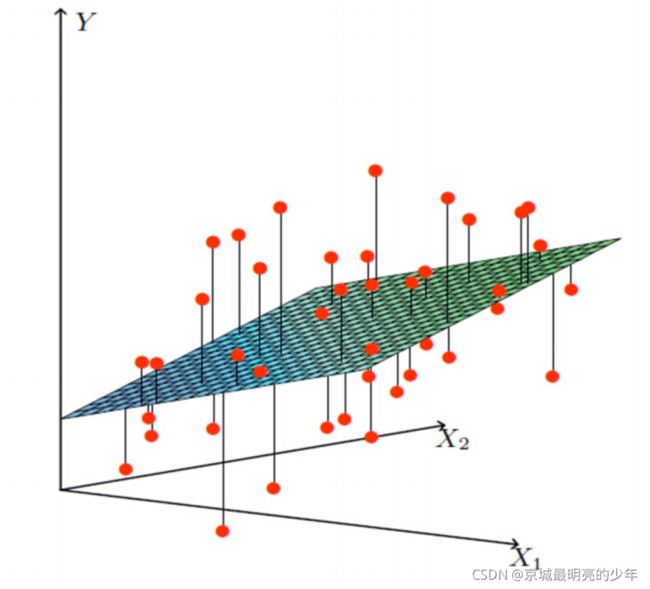
多变量的线性回归
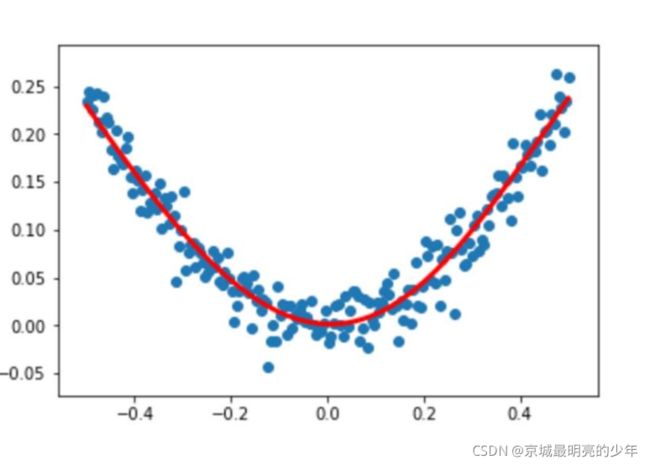
非线性回归
这种非线性回归可以理解为 y = w1x1+w2x22+ w3x33
3. 线性回归API示例
- sklearn.linear_model.LinearRegression()
- LinearRegression.coef_:回归系数
以学生的成绩为例子:
| 学生 | 平时成绩 | 期末成绩 | 最终成绩 |
|---|---|---|---|
| 1 | 80 | 86 | 84.2 |
| 2 | 82 | 80 | 80.6 |
| 3 | 85 | 78 | 80.1 |
| 4 | 90 | 90 | 90 |
| 5 | 86 | 82 | 83.2 |
| 6 | 82 | 90 | 87.6 |
| 7 | 78 | 80 | 79.4 |
通过上面的数据,我们怎么判断最终的成绩是通过什么样的一个比例算出总成绩的呢? 将设我们知道平时成绩和期末成绩,怎么计算出最终成绩呢,很多想到了解方程,没错这里其实就是一个二元一次方程,但是今天我们这里用Python的机器学习来计算这个问题。
from sklearn.linear_model import LinearRegression
def linner_model():
# 1、导入模块
# 2、创建数据
# x中存储的是平时成绩和期末成绩也就是特征值
x = [[80, 86],[82, 80], [85, 78], [90, 90], [86, 82], [82, 90], [78, 80], [92, 94]]
# y中存储的是最终成绩,也就是最终成绩
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
# 3、机器学习
# 3.1 创建API类
estimator = LinearRegression()
# 3.2 使用已有的数据训练一个模型出来
estimator.fit(x, y)
print("建模后的系数为:\n", estimator.coef_)
# 4、分数预测也就是对模型的使用
predict = estimator.predict([[80, 100]])
print("预测的值: \n", predict)
if __name__ == '__main__':
linner_model()
结果:

通过上面简单的例子我们可以建立这样数据模型,有人说这个很简单啊,是很简单,但是复杂的模型都是从这样一步步来的,基本原理没有变
4. 线性回归损失和优化

在上面这个图中我们可以看到,回归系数没有计算好就会出现较大的偏差,特别当数据大的时候,我们很可能就会出现偏差,那么怎么解决这个问题,就需要我们来计算损失进行优化了。
总损失为:

参数:yi表示第i个样本的真实值
hw(xi) 表示的是建模后预测的值
它还有一个最美的名字 【最小二乘法】,如果我们的预测模型hw(xi) 不准确,就会导致这个总损失函数的值变的非常大。
如果减小这个损失函数就是我们需要做的是,也就是有优化。
5. 优化算法
【1、正规⽅程】

理解:X为特征值矩阵,y为⽬标值矩阵。直接求到最好的结果 缺点:当特征过多过复杂时,求解速度太慢并且得不到结果。
这里的W是什么呢?很多人不理解,其实就是回归的系数
【标哥通俗话】:其实就是把总损失函数求最小值进而得到他的系数就是我们需要。

正规方程推导

6. 梯度下降(Gradient Descent)
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。

梯度是微积分中⼀个很重要的概念 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率。其实就是说沿着下降最快的方向走,直到走到山地,读者可以想一下,如果有个悬崖,那里的梯度肯定是最快的,这也就是梯度下降算法的特点。我们需要到达⼭底,就需要在每⼀步观测到此时最陡峭的地⽅,梯 度就恰巧告诉了我们这个⽅向。
6. 梯度下降举例
我们假设这样一个函数:J(θ) = θ2
函数的微分:J’(θ) = 2θ
初始化,起点为: θ(0) = 1
学习率:α = 0.4 就是系数
我们开始进⾏梯度下降的迭代计算过程:


上面介绍的是单变量,还有多变量的梯度算法,其实原理是一样的,只是多变量可以理解为平面,立体的情况,如:
J(θ) = θ12 + θ22
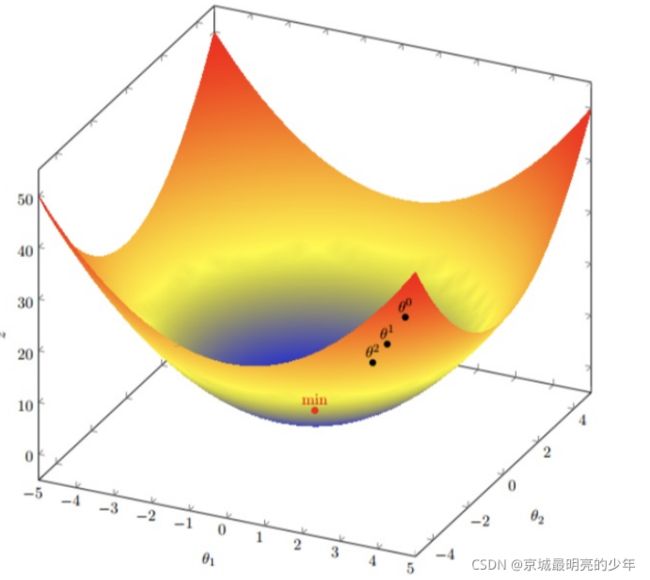
分析梯度下降算法的公式:
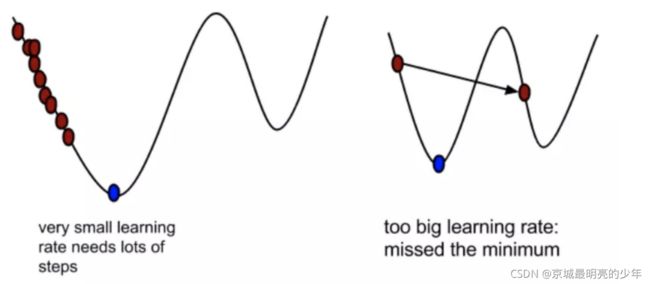
α :学习的步长,变化率,可以这么理解,意味着我们可以改变步长,但是又不能过分的改变步长,否者会出现下面这种情况
梯度下降算法和正规方程的对比
| 梯度下降 | 正规⽅程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | ⼀次运算得出 |
| 特征数量较⼤可以使⽤ | 需要计算⽅程,时间复杂度⾼O(n3) |
7. 梯度下降算法
1. 全梯度下降算法(Full gradient descent),
2. 随机梯度下降算法(Stochastic gradient descent),
3. 随机平均梯度下降算法(Stochastic average gradient descent)
4. 小批量梯度下降算法(Mini-batch gradient descent
它们都是为了正确地调节权重向量,通过为每个权重计算⼀个梯度,从⽽更新权值,使⽬标函数尽可能最⼩化。其差别 在于样本的使⽤⽅式不同。
1、全梯度下降算法
训练所有的样本误差,对其求和再取平均值作为目标函数
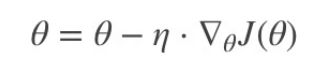
全体都下降算法就是全部的数据参加运算,这样就保证了每次都能朝这正确的方向进行,但是缺点就是所有的数据参加运算,消耗比较大,如果原始数据比较大,就不太现实用这个方法来实现
2. 随机梯度下降算法(Stochastic gradient descent)

因为是随机下降,每次就只训练一个数据,这样就会导致损失函数变化、波动比较大从而不能很好的判断损失函数是否收敛。
3. 小批量梯度下降算法(Mini-batch gradient descent

小批量梯度下降算法,就兼顾了上面两种算法的优点,克服了他们的缺点。
4. 随机平均梯度下降算法(Stochastic average gradient descent)
小批量梯度算法克服了成本和损失函数波动太大的问题,但是如果对于大数量的数据而言,每一份小批量数据之间还是区别很大的。那么随机平均梯度算法就克服了这个缺点。在内存中为每⼀个样本都维护⼀个旧的梯度,随机选择第i个样本来更新此样本的梯 度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进⽽更新了参数。
比较:
(1)FG⽅法由于它每轮更新都要使⽤全体数据集,故花费的时间成本最多,内存存储最⼤。
(2)SAG在训练初期表现不佳,优化速度较慢。这是因为我们常将初始梯度设为0,⽽SAG每轮梯度更新都结合了上 ⼀轮梯度值。
(3)综合考虑迭代次数和运⾏时间,SG表现性能都很好,能在训练初期快速摆脱初始梯度值,快速将平均损失函数降 到很低。但要注意,在使⽤SG⽅法时要慎重选择步⻓,否则容易错过最优解。
(4)mini-batch结合了SG的“胆⼤”和FG的“⼼细”,从6幅图像来看,它的表现也正好居于SG和FG⼆者之间。在⽬前 的机器学习领域,mini-batch是使⽤最多的梯度下降算法,正是因为它避开了FG运算效率低成本⼤和SG收敛效果不稳 定的缺点。
8. 线性回归API介绍
sklearn.linear_model.LinearRegression(fit_intercept=True) #通过正规⽅程优化
# fit_intercept:是否计算偏置
# LinearRegression.coef_:回归系数
# LinearRegression.intercept_:偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
# SGDRegressor类实现了随机梯度下降学习,它⽀持不同的loss函数和正则化惩罚项来拟合线性回归模型。
# loss:损失类型
# loss=”squared_loss”: 普通最⼩⼆乘法
# fit_intercept:是否计算偏置
# learning_rate : string,
# optional 学习率填充
'constant': eta = eta0
'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
'invscaling': eta = eta0 / pow(t, power_t)
power_t=0.25:存在⽗类当中 对于⼀个常数值的学习率来说,可以使⽤ learning_rate=’constant’ , 并使⽤eta0来指定学习率。
# SGDRegressor.coef_:回归系数
# SGDRegressor.intercept_:偏置
9.房价预测案例
使用均方误差来评估
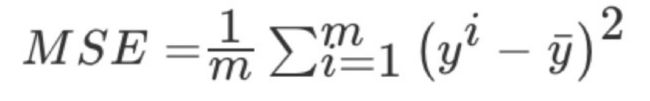
sklearn.metrics.mean_squared_error(y_true, y_pred)
均⽅误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
'''
正规方程
'''
def linner_model():
# 1、获取数据
boston = load_boston()
# 2、数据的基本处理
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)
# 3、特征工程,数据的标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4、机器学习,线性回归(正规方程)
estimator = LinearRegression()
estimator.fit(x_train, y_train)
# 5、模型评估
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 6 均方误差评价
error = mean_squared_error(y_test,y_predict)
print("误差为:\n",error)
'''
梯度下降算法
'''
def linner_model2():
# 1、获取数据
boston = load_boston()
# 2、数据的基本处理
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)
# 3、特征工程,数据的标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4、机器学习,线性回归(特征方程)
# max_iter 迭代次数
# eta0 学习率 0~1
# tol 终止条件
estimator = SGDRegressor(max_iter=1000)
estimator.fit(x_train, y_train)
# 5、模型评估
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 6 均方误差评价
score = estimator.score(x_test,y_test)
print("准确度为:\n",score)
error = mean_squared_error(y_test,y_predict)
print("误差为:\n",error)
if __name__ == '__main__':
linner_model2()
好了线性回归就讲这么多,其实这个应该是基础