Python机器学习13——主成分分析
本系列所有的代码和数据都可以从陈强老师的个人主页上下载:Python数据程序
参考书目:陈强.机器学习及Python应用. 北京:高等教育出版社, 2021.
本系列基本不讲数学原理,只从代码角度去让读者们利用最简洁的Python代码实现机器学习方法。
无监督学习就是没有y,让算法从特征变量x里面自己寻找特征。
本节开始无监督学习的方法,经典统计学的主成分分析,可以将数据进行线性变化从而进行降维,用少数几个变量代替原始的很多的变量。但是主成分不能进行变量筛选,因为新的变量是原始变量的线性组合,失去了原有的含义。而和主成分很像的因子分析可以进行部分解释。
主成分分析的Python案例
采用一个听力的数据集,导入包和数据:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d
audiometric = pd.read_csv('audiometric.csv')
audiometric.shape
audiometric.head()数据长这样
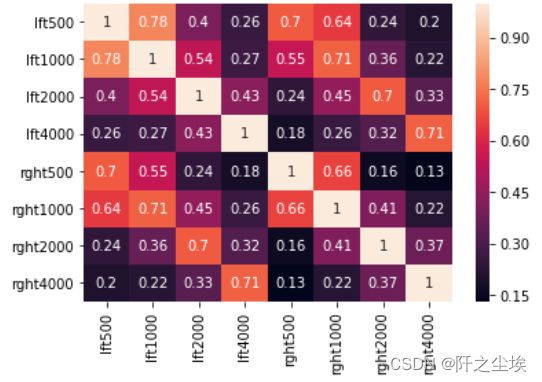
计算其相关系数
pd.options.display.max_columns = 10
round(audiometric.corr(), 2)画出相关系数矩阵热力图
sns.heatmap(round(audiometric.corr(), 2),annot=True)数据标准化
scaler = StandardScaler()
scaler.fit(audiometric)
X = scaler.transform(audiometric)主成分pca拟合
model = PCA()
model.fit(X)
#每个主成分能解释的方差
model.explained_variance_
#每个主成分能解释的方差的百分比
model.explained_variance_ratio_
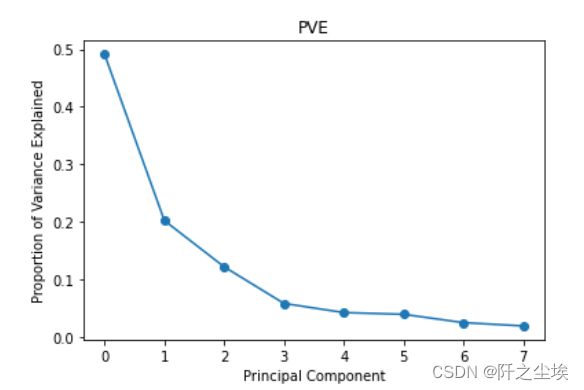
#可视化
plt.plot(model.explained_variance_ratio_, 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Proportion of Variance Explained')
plt.title('PVE')
画累计百分比,这样可以判断选几个主成分
plt.plot(model.explained_variance_ratio_.cumsum(), 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Cumulative Proportion of Variance Explained')
plt.axhline(0.9, color='k', linestyle='--', linewidth=1)
plt.title('Cumulative PVE')
4个主成分能解释到90%以上了
主成分核载矩阵
#主成分核载矩阵
model.components_
columns = ['PC' + str(i) for i in range(1, 9)]
pca_loadings = pd.DataFrame(model.components_, columns=audiometric.columns, index=columns)
round(pca_loadings, 2)该矩阵展示了每个主成分是原始数据的线性组合,以及线性的系数
画图展示
# Visualize pca loadings
fig, ax = plt.subplots(2, 2)
plt.subplots_adjust(hspace=1, wspace=0.5)
for i in range(1, 5):
ax = plt.subplot(2, 2, i)
ax.plot(pca_loadings['PC' + str(i)], 'o-')
ax.axhline(0, color='k', linestyle='--', linewidth=1)
ax.set_xticks(range(8))
ax.set_xticklabels(audiometric.columns, rotation=30)
ax.set_title('PCA Loadings for PC' + str(i))
计算每个样本的主成分得分
# PCA Scores
pca_scores = model.transform(X)
pca_scores = pd.DataFrame(pca_scores, columns=columns)
pca_scores.shape
pca_scores.head()
#前两个主成分的可视化
# visualize pca scores via biplot
sns.scatterplot(x='PC1', y='PC2', data=pca_scores)
plt.title('Biplot')
三个主成分的可视化,三维图
# Visualize pca scores via triplot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pca_scores['PC1'], pca_scores['PC2'], pca_scores['PC3'], c='b')
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
利用K均值聚类对三个主成分聚类,可视化
from sklearn.cluster import KMeans
model = KMeans(n_clusters=3, random_state=1, n_init=20)
model.fit(X)
model.labels_
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pca_scores['PC1'], pca_scores['PC2'], pca_scores['PC3'],
c=model.labels_, cmap='rainbow')
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
主成分回归Python案例
使用中国香港的季度增长率的数据集进行主成分回归,读取数据,考察形状
growth = pd.read_csv('growth.csv')
growth.shape
growth.head(3)
growth.tail(3)
x为和中国香港相邻或有密切来往的24个国家的经济增长率。
#设置时间索引
growth.index = growth['Quarter']
growth = growth.drop(columns=['Quarter'])
#计算香港和其他地区的相关系数
# Correlation between HK's growth rate and other countries
growth.corr().iloc[:, 0]划分训练测试集,手工划分,前44个数据作为训练集,后面测试集。然后标准化
X_train = growth.iloc[:44, 1:]
X_train.shape
X_test = growth.iloc[44:, 1:]
X_test.shape
y_train = growth.iloc[:44, 0]
y_test = growth.iloc[44:, 0]
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)使用留一交叉验证选择误差最小的时候的主成分个数
scores_mse = []
for k in range(1, 24):
model = PCA(n_components=k)
model.fit(X_train)
X_train_pca = model.transform(X_train)
loo = LeaveOneOut()
mse = -cross_val_score(LinearRegression(), X_train_pca, y_train,
cv=loo, scoring='neg_mean_squared_error')
scores_mse.append(np.mean(mse))
min(scores_mse)
index = np.argmin(scores_mse)
index
plt.plot(range(1, 24), scores_mse)
plt.axvline(index + 1, color='k', linestyle='--', linewidth=1)
plt.xlabel('Number of Components')
plt.ylabel('Mean Squared Error')
plt.title('Leave-one-out Cross-validation Error')
plt.tight_layout()主成分个数为6时最小,下面使用六个主成分回归
model = PCA(n_components = index + 1)
model.fit(X_train)
#得到主成分得分
X_train_pca = model.transform(X_train)
X_test_pca = model.transform(X_test)
X_train_pca
#进行线性回归拟合
reg = LinearRegression()
reg.fit(X_train_pca, y_train)
#全样本预测
X_pca = np.vstack((X_train_pca, X_test_pca))
X_pca.shape
pred = reg.predict(X_pca)
y = growth.iloc[:, 0]
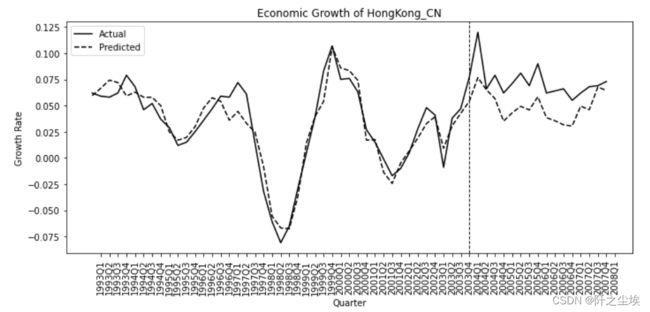
#可视化
plt.figure(figsize=(10, 5))
ax = plt.gca()
plt.plot(y, label='Actual', color='k')
plt.plot(pred, label='Predicted', color='k', linestyle='--')
plt.xticks(range(1, 62))
ax.set_xticklabels(growth.index, rotation=90)
plt.axvline(44, color='k', linestyle='--', linewidth=1)
plt.xlabel('Quarter')
plt.ylabel('Growth Rate')
plt.title("Economic Growth of HongKong_CN")
plt.legend(loc='upper left')
plt.tight_layout()
在44之前没有政策,曲线拟合效果好,44之后开始 政策实施,真实值大于拟合值,说明政策有效,促进了中国香港经济的发展。