【数据竞赛】基于LSTM模型实现共享自行车需求预测

公众号：尤而小屋
作者：Peter
编辑：Peter

今天给大家带来一篇新的kaggle数据分析实战案例：基于长短期记忆网络（LSTM）模型的伦敦自行车需求预测分析。本文的两个亮点：

• 高级可视化：本文使用seaborn进行了可视化探索分析，图表精美，分析维度多样化，结论清晰

• 使用LSTM模型：长短期网络模型的使用，使得结果更具价值和参考性

这是一个排名第三的方案：

感兴趣的可以参考原notebook地址进行学习：

https://www.kaggle.com/yashgoyal401/advanced-visualizations-and-predictions-with-lstm/notebook

还有一篇类似文章：

https://www.kaggle.com/geometrein/helsinki-city-bike-network-analysis

本文步骤

下面是原文中的主要步骤：数据信息、特征工程、数据EDA、预处理、模型构建、需求预测和评价模型

LSTM模型

本文重点是使用了LSTM模型。LSTM是一种时间递归神经网络，适合于处理和预测时间序列中间隔和延迟相对较长的重要事件。

小编实力有限，关于模型的原理详细讲解参考书籍和文章：

1、优秀书籍：《Long Short Term Memory Networks with Python》是澳大利亚机器学习专家Jason Brownlee的著作

2、知乎文章：https://zhuanlan.zhihu.com/p/24018768

3、B站：搜索李沐大神关于LSTM的讲解

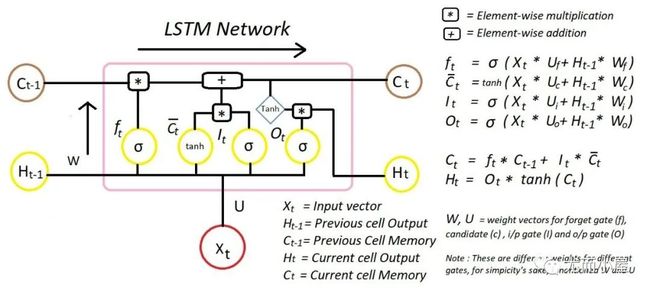
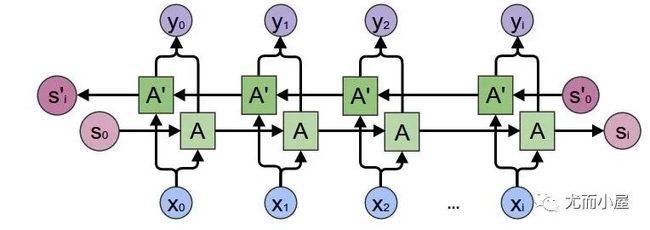
以后有实力了，肯定写一篇关于LSTM原理的文章！一起学习吧！卷！

数据

导入库

import pandas as pd
import numpy as np

# seaborn可视化
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(context="notebook", style="darkgrid", 
        palette="deep", font="sans-serif", 
        font_scale=1, color_codes=True)

# 忽略警告
import warnings
warnings.filterwarnings("ignore")

读取数据

基本信息：

# 1、数据量
data.shape

(17414, 10)

# 2、数据字段类型
data.dtypes

timestamp        object
cnt               int64
t1              float64
t2              float64
hum             float64
wind_speed      float64
weather_code    float64
is_holiday      float64
is_weekend      float64
season          float64
dtype: object

数据中没有缺失值：

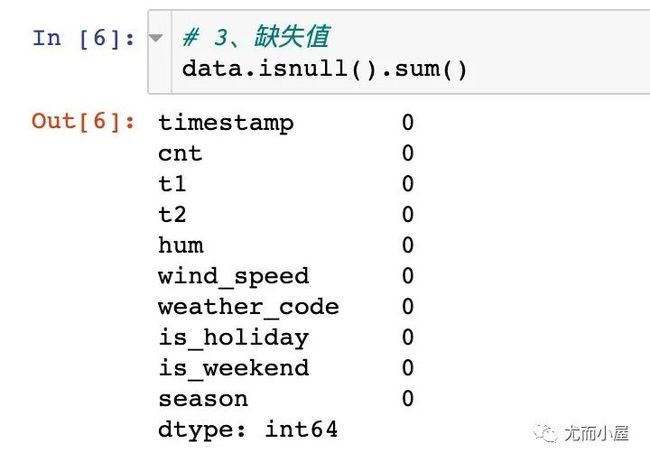
字段含义

解释下数据中字段的含义：

• timestamp：用于将数据分组的时间戳字段

• cnt：新自行车份额的计数

• t1：以C为单位的实际温度

• t2：C中的温度“感觉像”，主观感受

• hum：湿度百分比

• windspeed：风速，以km / h为单位

• weathercode：天气类别；（具体的取值见下图中的最后）

• isholiday：布尔字段，1-假期，0-非假期

• isweekend：布尔字段，如果一天是周末，则为1

• Season：类别气象季节：0-春季；1-夏；2-秋；3-冬

TensorFlow基本信息

TensorFlow的GPU信息和版本查看：

特征工程

下面介绍本文中特征工程的实现：

数据信息

一个DataFrame的info信息能够显示出字段名、非空数量、数据类型等多个基本信息

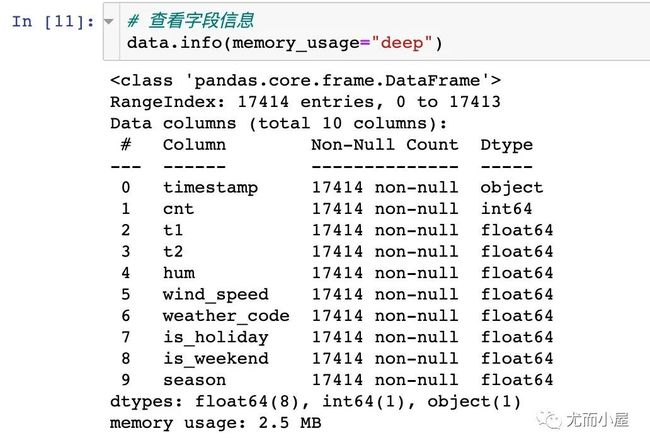
时间字段处理

对原始数据中的时间相关字段进行处理：

1、将时间戳转成时间类型

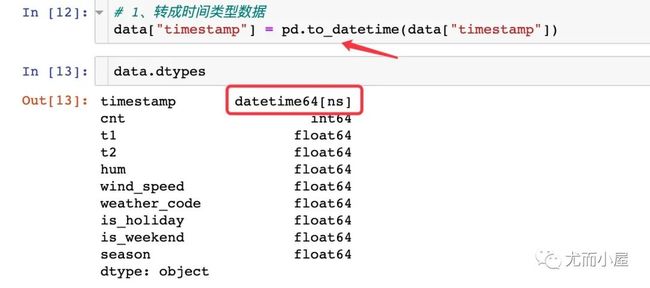
2、转成索引

使用set_index方法将timestamp属性转成索引

3、提取时、一个月中的第几天、第几周、月份等信息

提取时间相关的多个信息，同时查看数据的shape

相关系数分析

1、相关系数求出绝对值

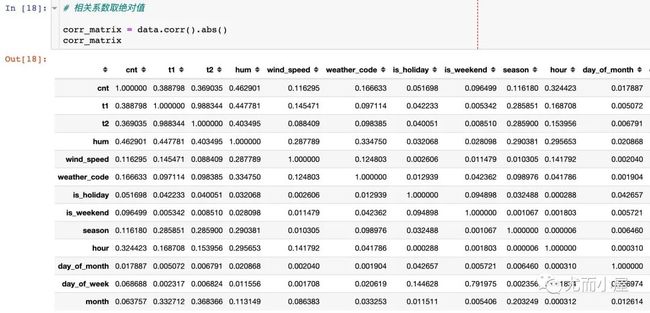
2、筛选两个属性之间的相关系数大于0.8

数据EDA

相关系数热力图

plt.figure(figsize=(16,6))

sns.heatmap(data.corr(),
            cmap="YlGnBu",  # 色系
            square=True,  # 方形
            linewidths=.2,
            center=0,
            linecolor="red"  # 线条颜色
           )

plt.show()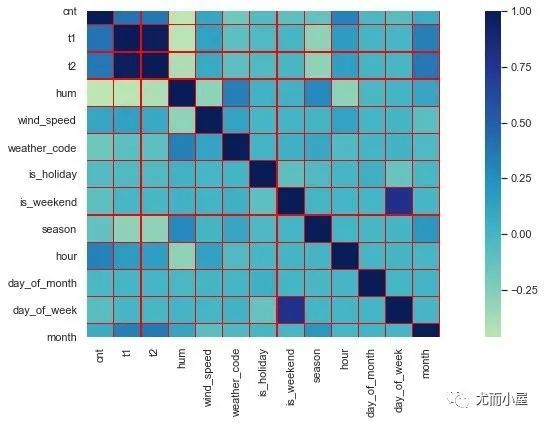

通过热力图我们发现：t1和t2的相关系数是比较高的，和上面的“属性之间的系数大于0.8”的结论是吻合的

空值判断

关于如何判断一份数据中是否存在空值，小编常用的方法：

文章中使用的方法是：基于热力图显示。图形中没有任何信息，表明数据是不存在空值的

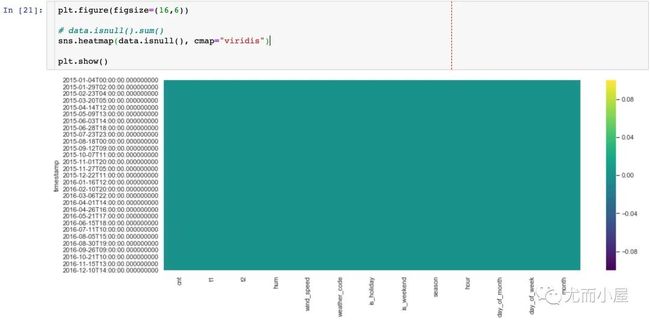
需求量变化

整体的需求量cnt随着时间变化的关系：

plt.figure(figsize=(15,6))

sns.lineplot(data=data,  # 传入数据
             x=data.index,  # 时间
             y=data.cnt  # 需求量
            )

plt.xticks(rotation=90)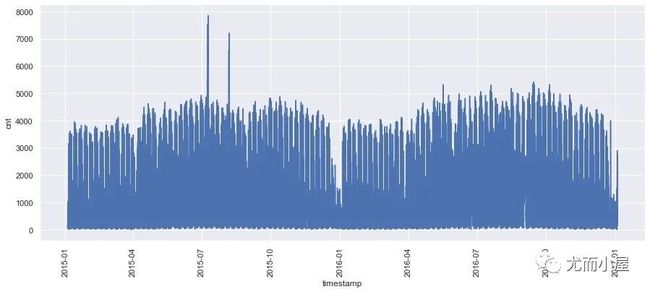

从上面的图形，我们能够看到整体日期下的需求量变化情况。

按月采样resample

pandas中的采样函数使用的是resample，频率可以是天、周、月等

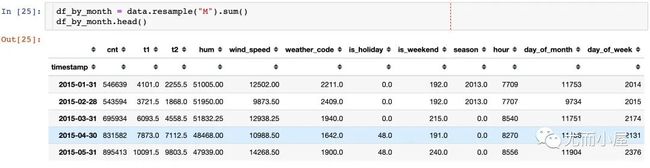
查看随着时间的变化，每月的需求量变化情况：

plt.figure(figsize=(16,6))

sns.lineplot(data=df_by_month,
             x=df_by_month.index,
             y=df_by_month.cnt,
             color="red"
            )

plt.xticks(rotation=90)

plt.show()

可以从图中观察到以下3点结论：

1. 年初到7、8月份需求量呈现上升趋势

2. 差不多在8月份达到一定的峰值

3. 8月份过后需求量开始降低

每小时需求量

plt.figure(figsize=(16,6))

sns.pointplot(data=data,  # 数据
              x=data.hour,  # 小时
              y=data.cnt,  # 需求量
              color="red"  # 颜色
             )

plt.show()

每月的需求量对比

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.month,
              y=data.cnt,
              color="red"
             )
plt.show()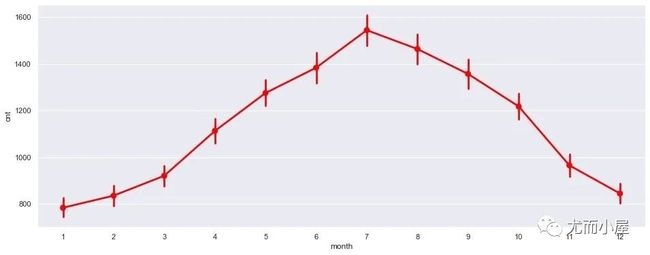

明显的结论：7月份是需求的高峰期

按照星期统计

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.day_of_week,
              y=data.cnt,
              color="black")

plt.show()

从图中观察到：

• 周1到周五的需求是明显高于周末两天；

• 同时在周五的时候已经呈现下降趋势

按照自然日

plt.figure(figsize=(16,6))

sns.lineplot(
  data=data,
  x=data.day_of_month,  # 一个月中的某天
  y=data.cnt,  # 需求量
  color="r")

plt.show()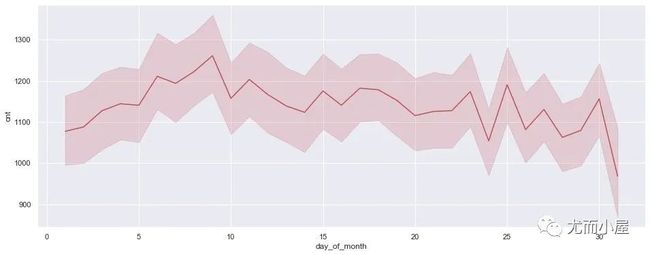

3点结论：

• 前10天需求量在逐步增加

• 中间10天存在一定的小幅波动

• 最后10天波动加大，呈现下降趋势

多个维度下的可视化化效果

基于是否节假日下的小时

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.hour,  # 按照小时统计
              y=data.cnt,
              hue=data.is_holiday  # 节假日分组
             )

plt.show()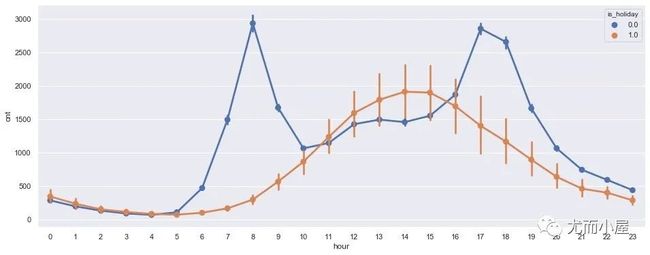

通过上面图形呈现的结果；

• 非节假日下（is_holiday=0）：在8点和下午的17、18点是用车的高峰期，恰好是上下班的时间点

• 到了节假日（1）的情况下：下午的2-3点才是真正的用车高峰期

基于是否节假日的月份

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.month,
              y=data.cnt,
              hue=data.is_holiday
             )

plt.show()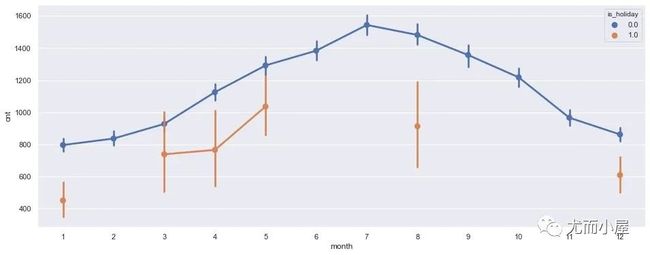

在非节假日，7月份达到了用车的高峰期

3、按照季度统计

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              y=data.cnt,
              x=data.month,
              hue=data.season, # 季度分组
             )

plt.show()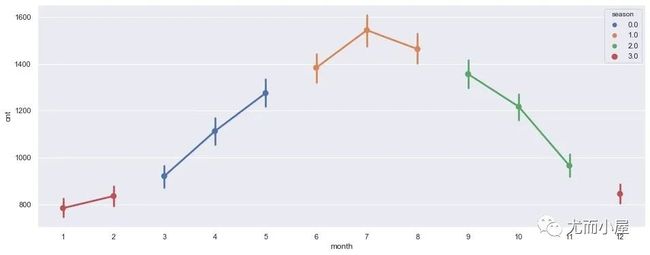

从上图中观察到：第3个季度（6–7-8月份）才是用车需求量最多的时候

4、季度+是否节假日

plt.figure(figsize=(16,6))

# 分组统计数量
sns.countplot(data=data,
              x=data.season,
              hue=data.is_holiday,
             )

plt.show()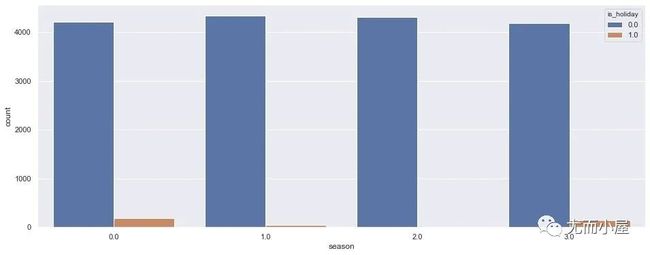

从1-2-3-4季度来看，非节假日中的整体需求量1和2季度是稍高于0和3季度；而节假日中，0-3季度则存在一定的需求

5、是否周末+小时

plt.figure(figsize=(16,6))

sns.lineplot(
    data=data,
    x=data.hour,  # 小时
    y=data.cnt,
    hue=data.is_weekend)  # 分是否周末统计

plt.show()

• 非周末（0）：仍然是上午的7-8点和下午的17-18点是用车高峰期

• 周末（1）：下午的14-15点才是高峰期

这个结论和上面的是吻合的

6、季度+小时

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.hour,
              y=data.cnt,
              hue=data.season # 分季度统计
             )

plt.show()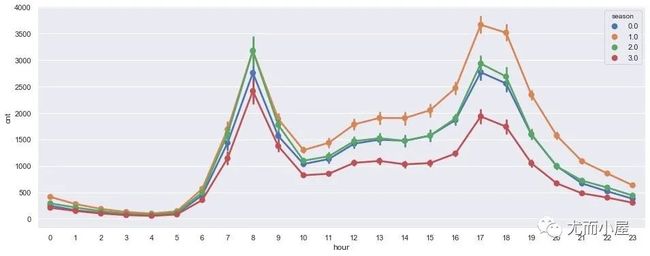

分季度查看每个小时的需求量：整体的趋势大体是相同的，都是在8点左右达到上午的高封期，下午的17-18点（下班的时候）达到另一个高封期

天气因素

湿度和需求量关系

观察不同湿度下，需求量的变化情况：

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.hum,
              y=data.cnt,
              color="black")

plt.xticks(rotation=90)

plt.show()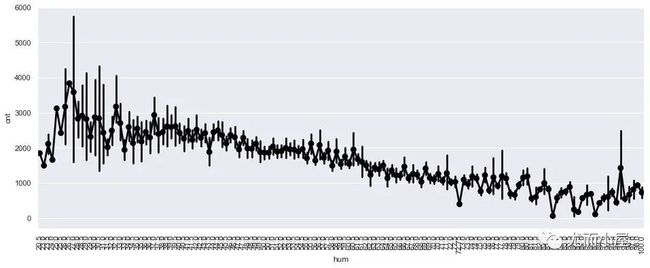

可以看到：空气空气湿度越大，整体的需求量是呈现下降趋势

风速和需求量

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.wind_speed,
              y=data.cnt)

plt.xticks(rotation=90)

plt.show()

风速对需求量的影响：

• 在风速为25.5的时候存在一个局部峰值

• 风速偏高或者偏低的时候需求都有所降低

不同天气情况weather_code

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.weather_code,
              y=data.cnt)

plt.xticks(rotation=90)

plt.show()

结论：可以看到在scattered coluds（weather_code=2）情况下，需求量是最大的

天气情况+小时

plt.figure(figsize=(16,6))

sns.pointplot(data=data,
              x=data.hour,
              y=data.cnt,
              hue=data.weather_code # 分天气统计
             )

plt.show()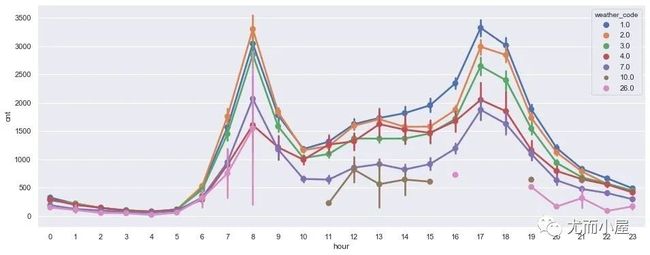

从上午中观察到：不同的天气对小时需求量的趋势影响不大，仍然是在上下班高峰期的时候需求量最大，说明打工人上班出行几乎不受天气影响！！！

自然天+天气情况

plt.figure(figsize=(16,6))

sns.countplot(
    data=data,
    x=data.day_of_week,  # 一周中的第几天
    hue=data.weather_code,  # 天气情况
    palette="viridis")

plt.legend(loc="best")  # 位置选择

plt.show()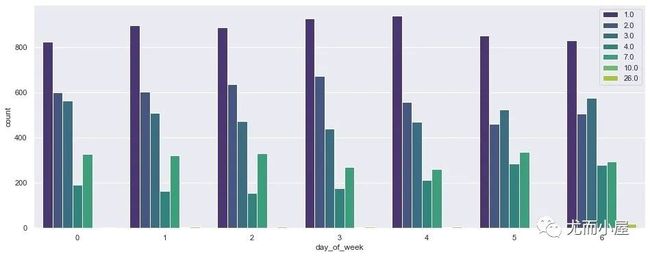

从上图中观察到：

1. 不同的星期日期，code=1下的需求量都是最大的

2. 礼拜1到礼拜5：满足code=1 > 2 > 3 > 7 > 4 的需求量

3. 到礼拜6和礼拜天：大家出行的时候对天气关注影响偏低，除去code=1，其他天气情况的需求差距也在缩小！

箱型图

箱型图能够反映一组数据的分布情况

按小时

plt.figure(figsize=(16,6))

sns.boxplot(data=data,
            x=data.hour,  # 小时
            y=data.cnt)

plt.show()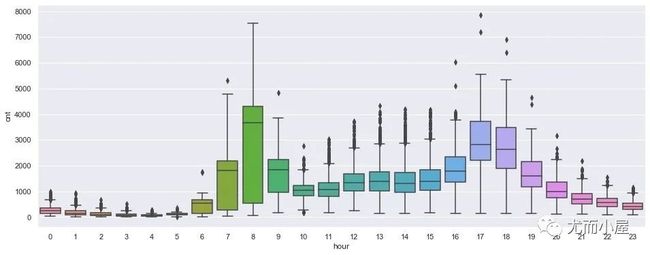

从箱型图的分布观察到：两个重要的时间段：上午7-8点和下午的17-18点

每周星期几

plt.figure(figsize=(16,6))

sns.boxplot(
    data=data,
    x=data["day_of_week"],
    y=data.cnt)

plt.show()

在基于星期的箱型图中，礼拜三的时候存在一定的用车高峰期

月的自然天

plt.figure(figsize=(16,6))

sns.boxplot(data=data,
            x=data["day_of_month"],
            y=data.cnt)

plt.show()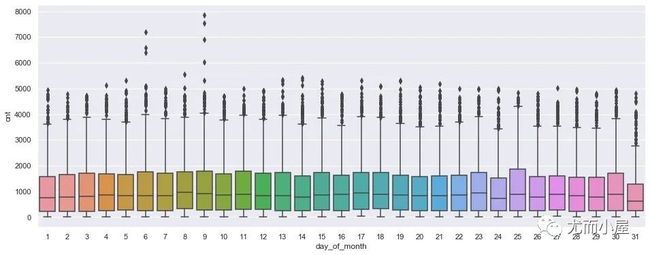

在基于自然日的情况下，9号的存在高峰期

按月

plt.figure(figsize=(16,6))

sns.boxplot(data=data,
            x=data["month"],
            y=data.cnt)

plt.show()

明显观察到：7-8月份存在一定的需求高峰期，两侧月份的需求相对较少些

是否节假日+月的天

# 每月中的天和是否节假日统计

plt.figure(figsize=(16,6))

sns.boxplot(
    data=data,
    x=data["day_of_month"],
    y=data.cnt,
    hue=data["is_holiday"])

plt.show()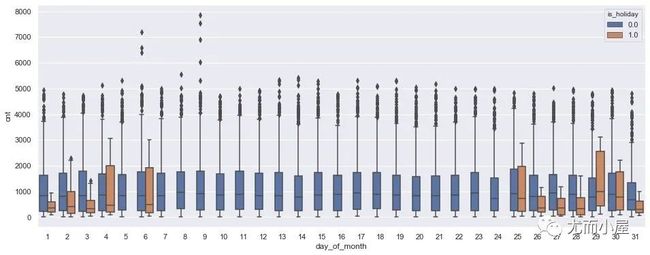

数据预处理

下面开始进行建模，首先进行的是数据预处理工作，主要是包含两点：

• 数据集的切分

• 数据归一化和标准化

切分数据

按照9：1的比例来切分数据集：

# 切分数据集的模块
from sklearn.model_selection import train_test_split
train,test = train_test_split(data,test_size=0.1, random_state=0)
print(train.shape)
print(test.shape)

# ------
(15672, 13)
(1742, 13)

数据归一化

from sklearn.preprocessing import MinMaxScaler
# 实例化对象
scaler  = MinMaxScaler()

# 部分字段的拟合
num_col = ['t1', 't2', 'hum', 'wind_speed']
trans_1 = scaler.fit(train[num_col].to_numpy())

# 训练集转换
train.loc[:,num_col] = trans_1.transform(train[num_col].to_numpy())
# 测试集转换
test.loc[:,num_col] = trans_1.transform(test[num_col].to_numpy())

# 对标签cnt的归一化
cnt_scaler = MinMaxScaler()
# 数据拟合
trans_2 = cnt_scaler.fit(train[["cnt"]])
# 数据转化
train["cnt"] = trans_2.transform(train[["cnt"]])
test["cnt"] = trans_2.transform(test[["cnt"]])

训练集和测试集

# 用于显示进度条
from tqdm import tqdm_notebook as tqdm
tqdm().pandas()

def prepare_data(X, y, time_steps=1):
    Xs = []
    Ys = []
    
    for i in tqdm(range(len(X) - time_steps)):
        a = X.iloc[i:(i + time_steps)].to_numpy()
        Xs.append(a)
        Ys.append(y.iloc[i + time_steps])
        
    return np.array(Xs), np.array(Ys)

steps = 24

X_train, y_train = prepare_data(train, train.cnt, time_steps=steps)
X_test, y_test = prepare_data(test, test.cnt, time_steps=steps)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

LSTM建模

导入库

在建模之前先导入相关的库：

# 1、导入需要的库
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Dropout, LSTM, Bidirectional

# 2、实例化对象并拟合建模
model = Sequential()
model.add(Bidirectional(LSTM(128, 
                             input_shape=(X_train.shape[1],
                                          X_train.shape[2]))))

model.add(Dropout(0.2))
model.add(Dense(1, activation="sigmoid"))
model.compile(optimizer="adam", loss="mse")

模型准备

传入训练集的数据后，进行数据的拟合建模过程：

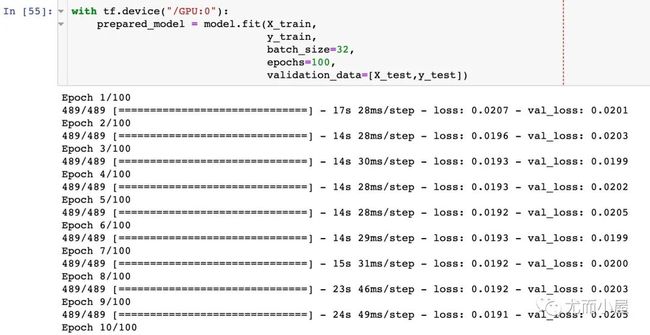
均方差和Epoch的关系

探索在不同的Epoch下均方差的大小：

plt.plot(prepared_model.history["loss"],label="loss")
plt.plot(prepared_model.history["val_loss"],label="val_loss")

# lengend位置选择
plt.legend(loc="best")
# 两个轴的标题
plt.xlabel("No. Of Epochs")
plt.ylabel("mse score")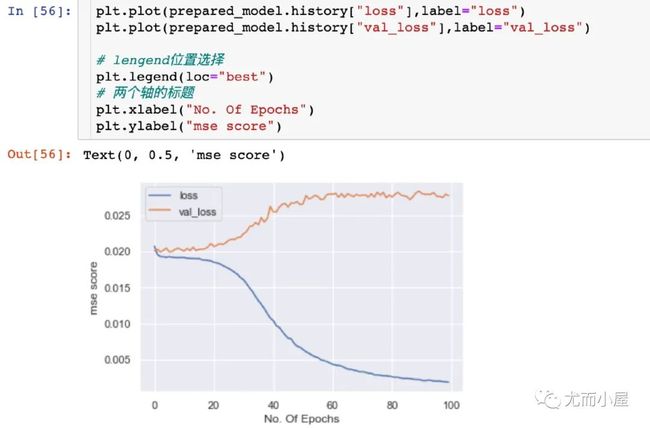

需求量预测

生成真实值和预测值

inverse_transform 函数是将标准化后的数据转换为原始数据。

pred = model.predict(X_test)  # 对测试集预测 
y_test_inv = cnt_scaler.inverse_transform(y_test.reshape(-1,1))  # 转变数据
pred_inv = cnt_scaler.inverse_transform(pred)  # 预测值转换
pred_inv

绘图比较

将测试集转变后的值和基于模型的预测值进行绘图比较：

plt.figure(figsize=(16,6))

# 测试集：真实值
plt.plot(y_test_inv.flatten(), marker=".", label="actual")
# 模型预测值
plt.plot(pred_inv.flatten(), marker=".", label="predicttion",color="r")
# 图例位置
plt.legend(loc="best")
plt.show()

生成数据

将测试集的真实值和预测值进行对比，通过两个指标来进行评估：

1、原文中的方法（个人认为复杂了）：

# 原方法过程复杂了

y_test_actual = cnt_scaler.inverse_transform(y_test.reshape(-1,1))
y_test_pred = cnt_scaler.inverse_transform(pred)

arr_1 = np.array(y_test_actual)
arr_2 = np.array(y_test_pred)

actual = pd.DataFrame(data=arr_1.flatten(),columns=["actual"])
predicted = pd.DataFrame(data=arr_2.flatten(),columns = ["predicted"])

final = pd.concat([actual,predicted],axis=1)
final.head()

2、个人方法

y_test_actual = cnt_scaler.inverse_transform(y_test.reshape(-1,1))
y_test_pred = cnt_scaler.inverse_transform(pred)
final = pd.DataFrame({"actual": y_test_actual.flatten(),
                      "pred": y_test_pred.flatten()})
final.head()

模型评价

通过mse和r2_score指标来评估模型：

# mse、r2_score
from sklearn.metrics import mean_squared_error, r2_score

rmse = np.sqrt(mean_squared_error(final.actual, final.pred))
r2 = r2_score(final.actual, final.pred)

print("rmse is : ", rmse)
print("-------")
print("r2_score is : ", r2)

# 结果
rmse is :  1308.7482342002293
-------
r2_score is :  -0.3951062293743659

下面作者又绘图来对比真实值和预测值：

plt.figure(figsize=(16,6))

# 真实值和预测值绘图
plt.plot(final.actual, marker=".", label="Actual label")
plt.plot(final.pred, marker=".", label="predicted label")
# 图例位置
plt.legend(loc="best")

plt.show()

疑点

Peter个人有个疑点：下面的两幅图有什么区别，除了颜色不同？看了整个源码，作图的数据和代码都是一样的。作者还写了两段话：

Note that our model is predicting only one point in the future. That being said, it is doing very well. Although our model can’t really capture the extreme values it does a good job of predicting (understanding) the general pattern.

说普通话：注意到，我们的模型仅预测未来的一个点。话虽如此，它仍做得很好。虽然我们的模型不能真正捕捉到极值，但它在预测（理解）一般模式方面还是做得很好

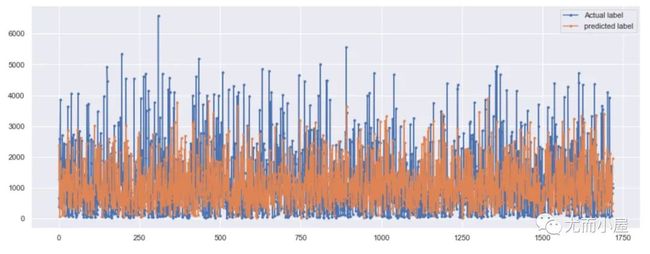
AS you can see that I have used Bidirectional LSTM to train our model and Our model is working quite well.Our model is cap*able to capture the trend and not capturing the Extreme values which is a really good thing. SO, we can say that the overall perfomance is good.

说普通话：如你所见，我使用双向 LSTM 来训练我们的模型，并且我们的模型运行良好。我们的模型能够捕捉趋势而不是捕捉极值，这是一件非常好的事情。所以，我们可以说整体表现不错。

下面是整个建模的源码，请参考学习，也可以讨论上面的疑点：

# 划分数据集
from sklearn.model_selection import train_test_split
train,test = train_test_split(data,test_size=0.1,random_state=0)

# 数据归一化
from sklearn.preprocessing import MinMaxScaler
scaler  = MinMaxScaler()
# 对4个自变量的归一化
num_colu = ['t1', 't2', 'hum', 'wind_speed']
trans_1 = scaler.fit(train[num_colu].to_numpy())
train.loc[:,num_colu] = trans_1.transform(train[num_colu].to_numpy())
test.loc[:,num_colu] = trans_1.transform(test[num_colu].to_numpy())
# 对因变量的归一化
cnt_scaler = MinMaxScaler()
trans_2 = cnt_scaler.fit(train[["cnt"]])
train["cnt"] = trans_2.transform(train[["cnt"]])
test["cnt"] = trans_2.transform(test[["cnt"]])

# 导入建模库和实例化
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Dropout , LSTM , Bidirectional 
# 时序对象的实例化
model = Sequential()
model.add(Bidirectional(LSTM(128,input_shape=(X_train.shape[1],X_train.shape[2]))))
model.add(Dropout(0.2))
model.add(Dense(1,activation="sigmoid")) # 激活函数选择
model.compile(optimizer="adam",loss="mse")  # 优化器和损失函数选择

with tf.device('/GPU:0'):
    prepared_model = model.fit(X_train,
                               y_train,
                               batch_size=32,
                               epochs=100,
                               validation_data=[X_test,y_test])
    
# 两种损失的对比
plt.plot(prepared_model.history["loss"],label="loss")
plt.plot(prepared_model.history["val_loss"],label="val_loss")
plt.legend(loc="best")
plt.xlabel("No. Of Epochs")
plt.ylabel("mse score")

# 测试数据集的预测
pred = model.predict(X_test)  

# cnt数据的还原
y_test_inv = cnt_scaler.inverse_transform(y_test.reshape(-1,1))
pred_inv = cnt_scaler.inverse_transform(pred)

# 绘图1
plt.figure(figsize=(16,6))
plt.plot(y_test_inv.flatten(), marker=".",label="actual")
plt.plot(pred_inv.flatten(), marker=".",label="prediction",color="r")

# cnt数据的还原
y_test_actual = cnt_scaler.inverse_transform(y_test.reshape(-1,1))
y_test_pred = cnt_scaler.inverse_transform(pred)

# 转成数组
arr_1 = np.array(y_test_actual)
arr_2 = np.array(y_test_pred)

# 生成Pandas的DataFrame，合并数据
actual = pd.DataFrame(data=arr_1.flatten(),columns=["actual"])
predicted = pd.DataFrame(data=arr_2.flatten(),columns = ["predicted"])
final = pd.concat([actual,predicted],axis=1)

# 评价指标
from sklearn.metrics import mean_squared_error, r2_score
rmse = np.sqrt(mean_squared_error(final.actual,final.predicted)) 
r2 = r2_score(final.actual,final.predicted) 
print("rmse is : {}\nr2 is : {}".format(rmse,r2))

# 绘图2
plt.figure(figsize=(16,6))
plt.plot(final.actual,label="Actual data")
plt.plot(final.predicted,label="predicted values")
plt.legend(loc="best")

文中数据的获取方式，关注公众号【尤而小屋】，回复 自行车 即可。

或者百度云下载，链接: https://pan.baidu.com/s/1x_ZkXQJIrgyjkJ7Sko8lmA 

提取码: igoc

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载中国大学慕课《机器学习》（黄海广主讲）机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑
AI基础下载机器学习交流qq群955171419，加入微信群请扫码：