Logistic 回归算法原理及python代码实现(二分类模型)
使用场景
通常面临的二分类问题可能是:一封邮件是否为垃圾邮件;那么可以抽象成数字标签:
- y=0 表示负类->垃圾邮件
- y=1 表示正类->正常邮件
模型的提出
这要求数学模型的结果取值要在[0,1]范围内,通常线性回归 h ( θ ) h(\theta) h(θ)的取值范围是实数域,很容易取到 h ( θ ) > 1 h(\theta)>1 h(θ)>1或 h ( θ ) < 0 h(\theta)<0 h(θ)<0。需要一个函数将 h ( θ ) h(\theta) h(θ)的取值范围控制在[0,1]范围内。
sigmoid函数就具有这个良好性质:
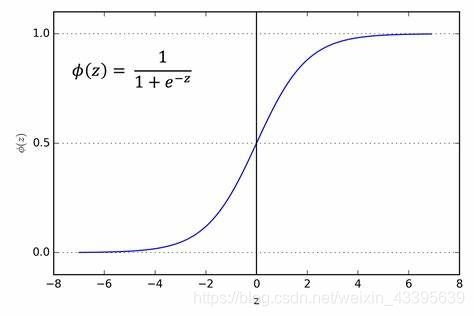
将线性模型 w T x w^{^{T}}x wTx代入sigmoid函数,所以新的假设函数 h ( w T x ) = 1 1 + e − w T x h (w ^{^{T}}x)=\frac{1}{1+e^{-w ^{^{T}}x}} h(wTx)=1+e−wTx1的取值范围是[0,1]。
- h ( w T x ) h (w ^{^{T}}x) h(wTx)>0.5,数据被分为1类。
- h ( w T x ) h (w^{^{T}}x) h(wTx)<0.5,数据被分为0类。
- h ( w T x ) h (w ^{^{T}}x) h(wTx)可以看成是分类的概率有多大。
这里的 w T w ^{^{T}} wT是每个特征的回归系数构成的向量, w T x = w 0 x 0 + w 1 x 1 + . . . w n x n w ^{^{T}}x=w_{0}x_{0}+w_{1}x_{1}+...w_{n}x_{n} wTx=w0x0+w1x1+...wnxn其中 x x x即为输入数据,这里共有n个特征,我们的目的是找到每个特征的最佳 w w w参数。
给定数据x,令其分为1类的概率 P ( Y = 1 ∣ x ) = h ( w T x ) = 1 1 + e − w T x P(Y=1|x)=h (w ^{^{T}}x)=\frac{1}{1+e^{-w ^{^{T}}x}} P(Y=1∣x)=h(wTx)=1+e−wTx1那么分为0类的概率即为 P ( Y = 0 ∣ x ) = 1 − P ( Y = 1 ∣ x ) P(Y=0|x)=1-P(Y=1|x) P(Y=0∣x)=1−P(Y=1∣x):
- P ( Y = 1 ∣ x ) = e w x 1 + e w x P(Y=1|x)=\frac{e^{wx}}{1+e^{wx}} P(Y=1∣x)=1+ewxewx
- P ( Y = 0 ∣ x ) = 1 1 + e w x P(Y=0|x)=\frac{1}{1+e^{wx}} P(Y=0∣x)=1+ewx1
Logistics回归也叫做对数几率回归
- 几率(odd):该事件发生的概率与不发生的概率的比值 p 1 − p \frac{p}{1-p} 1−pp
- 对数几率,即使对几率求对数, l o g i t ( p ) = l o g p 1 − p logit(p)=log\frac{p}{1-p} logit(p)=log1−pp
对logistic回归而言, l o g i t ( p ) = l o g P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w x logit(p)=log\frac{P(Y=1|x)}{1-P(Y=1|x)}=wx logit(p)=log1−P(Y=1∣x)P(Y=1∣x)=wx(将上述P(Y=1|x)带入即可得到,推导略),结果刚好是我们要训练的线性模型。
构建损失函数
模型建好以后,通常要构建损失函数,使最终的模型参数达到最优。损失函数表示估计结果与真实结果之间的差距,这个差距叫做损失,最优的目标是让损失最小,即求得损失函数最小值。
1. 考虑优化目标:
既然模型 h ( w T x ) h (w^{^{T}}x) h(wTx)可以看成是分类的概率,那么目标是让正确分类的概率最大。可以构建似然函数: ∏ i = 1 N [ h ( x i ) ] y i [ 1 − h ( x i ) ] 1 − y i \prod_{i=1}^{N}[h(x_{i})]^{yi}[1-h(x_{i})]^{1-yi} ∏i=1N[h(xi)]yi[1−h(xi)]1−yi
- N表示N个训练数据。
- h ( x i ) h(x_{i}) h(xi)表示给定数据x预测为1类的概率,yi表示训练数据的真实分类。 [ 1 − h ( x i ) ] [1-h(x_{i})] [1−h(xi)]表示给定数据x预测为0类的概率。
- 如果分类正确,则乘积保留正确分类的概率,比如yi=0, h ( x i ) y i = 1 h(x_{i})^{yi}=1 h(xi)yi=1,只保留 [ 1 − h ( x i ) ] 1 − y i = [ 1 − h ( x i ) ] = P ( Y = 0 ∣ x ) [1-h(x_{i})]^{1-yi}=[1-h(x_{i})]=P(Y=0|x) [1−h(xi)]1−yi=[1−h(xi)]=P(Y=0∣x)
这样最终的结果,就是所有正确分类的可能性乘积,数值越大越好。
2.构建损失函数
- 上述似然函数都是连乘,不便于计算,因此对整个结构取对数,将连乘变为连加。
- 另一方面,将上述求最大值问题加负号,就变成了最小化问题。
损失函数:
- J ( w ) = − ∑ i = 1 N [ y i l o g h ( x i ) + ( 1 − y i ) l o g ( 1 − h ( x i ) ) ] J\left ( w \right )=- \sum_{i=1}^{N}\left [y_{i}logh(x_{i})+(1-y_{i})log(1-h(x_{i})) \right ] J(w)=−∑i=1N[yilogh(xi)+(1−yi)log(1−h(xi))]
- J ( w ) = − ∑ i = 1 N [ y i ( w x i ) − l o g ( 1 + e w x i ) ) ] J\left ( w \right )=- \sum_{i=1}^{N}\left [y_{i}(wx_{i})-log(1+e^{wx_{i}})) \right ] J(w)=−∑i=1N[yi(wxi)−log(1+ewxi))]
最终 J ( w ) J\left ( w \right ) J(w)的括号内部,是所有数据正确分类的可能性的总和。这个总和越大,损失函数值越小。
优化
通过梯度下降法,不断优化参数 w w w,X为NxK的矩阵,y为N维列向量,h(X)也为估计列向量。 w w w为K维列向量。(N:训练样本数,K:特征数量)
J ( w ) J\left ( w \right ) J(w)对 w w w求偏导可以得:
-
∂ J ( w ) ∂ w k = ∑ i = 1 N x i k [ h ( x i ) − y i ] \frac{\partial J(w)}{\partial w_{k}}=\sum_{i=1}^{N}x_{ik}[h(x_{i})-y_{i}] ∂wk∂J(w)=∑i=1Nxik[h(xi)−yi]
-
∂ J ( w ) ∂ w = X T [ h ( X ) − y ] \frac{\partial J(w)}{\partial w} = X^{T}[h(X)-y] ∂w∂J(w)=XT[h(X)−y]
-
w n + 1 = w n − α ∂ J ( w ) ∂ w w_{n+1} = w_{n}-\alpha \frac{\partial J(w)}{\partial w} wn+1=wn−α∂w∂J(w)
代码实现
梯度下降方法找到最佳分类参数
# 基础包
import numpy as np
import seaborn as sns #一个基于matplotlib的便捷可视化工具
import pandas as pd
import matplotlib.pyplot as pltdef loadDataSet():
#导入数据集
data = []; label = []
file = open('testSet.txt')
for line in file.readlines():
lineArr = line.strip().split()
data.append([1.0, float(lineArr[0]), float(lineArr[1])])
label.append(int(lineArr[2]))
data = np.array(data)
label = np.array(label)
return data,label数据集情况:前两列为特征,第三列为分类标签
链接:https://pan.baidu.com/s/1169Bc7NWtqdxUxaiaPPaog
提取码:pnqe
def sigmoid(z):
return np.exp(z)/(1.0+np.exp(z))
def gradDcent(features,lable):
# 梯度下降法训练参数
# 初始化
X = np.mat(features)
y = np.mat(lable).T # 将标签处理为列向量
m,n = np.shape(X)
alpha = 0.001 # 步长
maxCycles = 500 # 循环次数
weights = np.ones((n,1)) # 特征参数
# 循环500次后停止迭代
for k in range(maxCycles):
h = sigmoid(X*weights) # 预测值
error = h - y
weights = weights - alpha*X.T*error #
return weightsX,y = loadDataSet()
weights = gradDcent(X,y)def PlotFit(X,y,weights):
# 分类数据可视化
df = pd.Dataframe(np.hstack((X,np.mat(y).transpose()),columns=['X0','X1','X2','Y'])
sns.scatterplot(x='X1',y='X2',hue='Y',data=df)
# 分类线
x_h = np.arange(-3.0,3.0,0.1)
y_h = np.array((-weights[0]-weights[1]*x)/weights[2])[0]
sns.lineplot(x=x_h,y=y_h)
PlotFit(X,y,weights)【小结】
迭代过程都是向量的运算,处理了所有的数据(批处理)X*weights有三个特征与权重相乘,100数据点,一共进行了300次的运算;同理,在权重的更新也是在每次迭代时计算所有数据,当数据量增大时,不便于迭代计算。(迭代次数*样本量)
算法改进
- 随机梯度下降方法:一次仅用一个样本点更新参数(回归系数)。
- 每次迭代,步长 α \alpha α随迭代次数不断变小。
- 这里当迭代次数<<样本个数的时候,alpha不是严格下降的,这样避免局部最优解
- 根据单样本训练模型时,打乱样本,避免周期性波动。
def stocGradDcent(X,y,iterNum=20): #默认迭代20次
m,n = np.shape(X)
weights = np.ones(n)
w0 = []
w1 = []
w2 = []
for j in range(iterNum):
dataIndexs = np.random.permutation(m) #打乱样本
for i in range(m): #根据打乱样本,依次取样,训练参数
alpha = 0.01 +4/(1.0+j+i)
index = dataIndexs[i]
h = sigmoid(np.sum(X[index]*weights))
error = h - y[index]
weights = weights - alpha*error*X[index].T
w0.append(weights[0])
w1.append(weights[1])
w2.append(weights[2])
df = pd.DataFrame({'w0':w0,
'w1':w1,
'w2':w2})
return df,weights X,y = loadDataSet()
weights = stocGradDcent(X,y)
plotFit(X,y,weights=weights)- 之前500次的结果,现在只需要迭代20次,即有较好的分类结果。
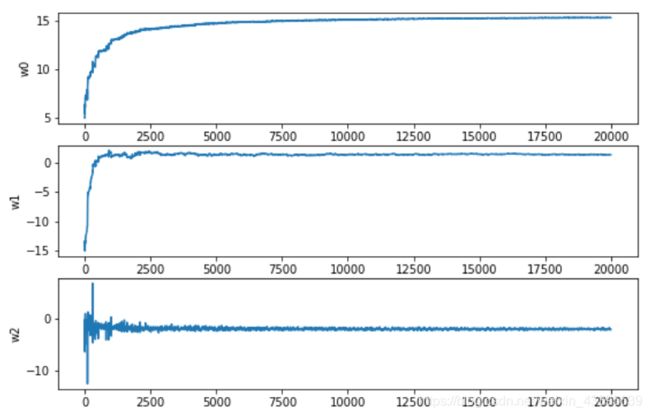
参数的收敛性
plt.figure(figsize=(15,10))
ax1 = plt.subplot2grid((3,1), (0, 0), colspan=1,rowspan=1)
sns.lineplot(x=df.index,y='w0',data=df,ax=ax1)
ax2 = plt.subplot2grid((3,1), (1, 0), colspan=1,rowspan=1)
sns.lineplot(x=df.index,y='w1',data=df)
ax3 = plt.subplot2grid((3,1), (2, 0), colspan=1,rowspan=1)
sns.lineplot(x=df.index,y='w2',data=df) 横坐标为训练次数,大概在2000次(迭代20次)左右,参数已经收敛。
总结
Logistic回归的目的是通过非线性函数sigmoid,找到一条最佳的分类线。优化目标是使预测样本正确分类的概率最大,通过梯度下降算法优化过程。考虑到面对大量数据进行分类时,批处理的计算量大,采用随机梯度下降的方式能够有效的训练回归参数,并降低计算量。