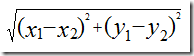k-近邻算法(KNN)
KNN的介绍
kNN(k-nearest neighbors),中文翻译K近邻。我们常常听到一个故事:如果要了解一个人的经济水平,只需要知道他最好的5个朋友的经济能力, 对他的这五个人的经济水平求平均就是这个人的经济水平。这句话里面就包含着kNN的算法思想。
如上图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
中心思想:knn常用于解决二分类问题,找到未分类的测试样本附近K个最相近的2分类的样本,该样本的分类由附近已分类的样本投票决定。
knn算法没有训练过程,相比于贝叶斯分类器,knn算法误差的上界不大于贝叶斯最优分类器误差的两倍。
KNN建立过程
1)给定测试样本,计算它与训练集中的每一个样本的距离。
2)按距离升序排序,取TOPk个最相近的训练数据。
3)取频率最高的类别作为测试数据的预测类别。
k值的选择
k为经验值,通常情况下k取奇数,当样本数量n较小时,k常在(1,10]中取,当样本数量较大时,k常在(1,sqrt(n))
距离度量
1.曼哈顿距离
2.欧氏距离
优缺点以及改进
优点:非常简单,易于实现,适合分类问题,有较高的准确度,对异常值不敏感
缺点:计算复杂,占用空间多,不适合样本数量很大的数据集
缺陷一:计算未分类点与所有已分类的点距离,再进行排序,导致计算量大
改进:使用kd数据结构,优化搜索操作,减少计算量
缺陷二:样本不平衡问题会影响分类结果
改进:采用权值的方法(距离的倒数)
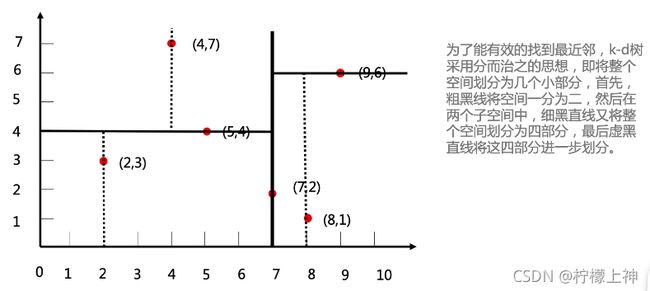
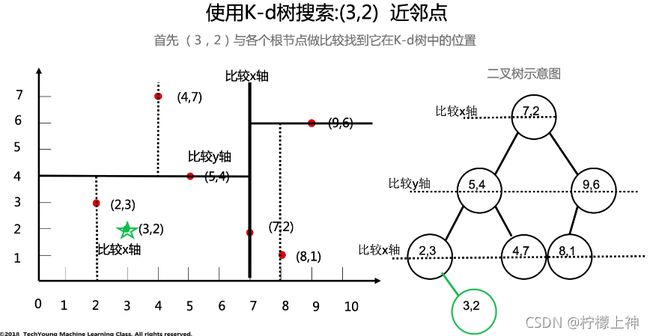
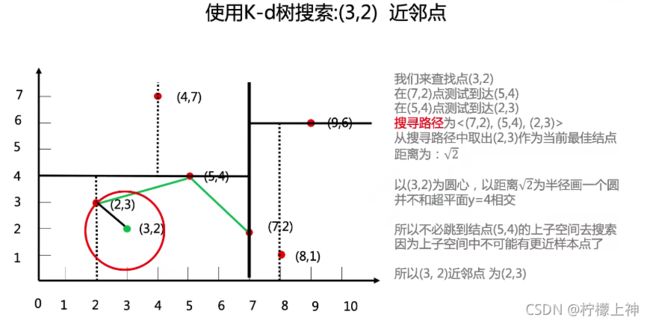
kd树
英文全称:K-Dimension Tree,对数据点在k维空间中划分的一种数据结构
中心思想: k-d树是一种空间划分树,把整个空间划分为特定的几个部分,然后在特定空间的部分内进行相关搜索操作
KNN的应用
KNN虽然很简单,但是人们常说"大道至简",一句"物以类聚,人以群分"就能揭开其面纱,看似简单的KNN即能做分类又能做回归, 还能用来做数据预处理的缺失值填充。由于KNN模型具有很好的解释性,一般情况下对于简单的机器学习问题,我们可以使用KNN作为 Baseline,对于每一个预测结果,我们可以很好的进行解释。推荐系统的中,也有着KNN的影子。例如文章推荐系统中, 对于一个用户A,我们可以把和A最相近的k个用户,浏览过的文章推送给A。
代码实现
import numpy as np
import math
import matplotlib.pyplot as plt
file = open('LRdata.txt')
x = []
y = []
for line in file.readlines():
line = line.strip().split()
x.append([float(line[0]), float(line[1])])
y.append(float(line[-1]))
xmat = np.mat(x)
ymat = np.mat(y).T
file.close()
# 计算距离并排序
k = 5 # 定义k值
t = list(map(int, input("请输入二维坐标:").split()))
t = np.array(t)
a = xmat - t
list1 = []
for i in range(a.shape[0]):
b = math.sqrt(a[i, 0] ** 2 + a[i, 1]**2)
list1.append(b)
# 排序算法
sort = np.array(list1).argsort()
# 提取前k位标签
list2 = []
for i in range(len(sort)):
if sort[i] < k:
list2.append(y[i])
label = max(list2, key=list2.count)
print(label)
# show
plt.scatter(xmat[:, 0][ymat == 0].A, xmat[:, 1][ymat == 0].A, marker='^', s=150)
plt.scatter(xmat[:, 0][ymat == 1].A, xmat[:, 1][ymat == 1].A, marker='o', s=150)
if label == 0:
plt.scatter(t[0], t[1], marker='^', s=150, c='g')
else:
plt.scatter(t[0], t[1], marker='o', s=150, c='g')
plt.show()