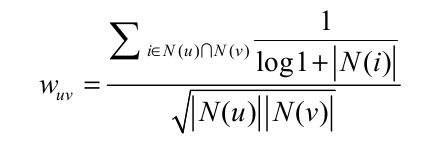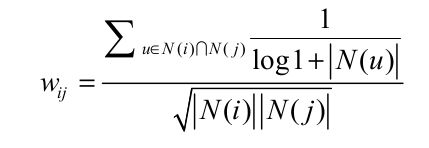第二章 利用用户行为数据
2.1 用户行为简介
用户的行为分为显性反馈行为以及隐性反馈行为.用产生行为的用户和行为的对象、行为的种类、产生行为的上下文、行为的内容和权重六个部分表示用户的行为.安装上述定义可将数据集分为:无上下文的隐性反馈数据集;无上下文信息的显性反馈数据集;有上下文的隐性反馈数据集;有上下文信息的显性反馈数据集.
2.2 用户行为分析
(1) 互联网上的很多数据存在PowerLaw分布($f(x) = ax^k$),也叫长尾分布,意思是小部分个体的值比较小,绝大多数个体的值比较小(比如热门的商品用户量很多,但是热门商品占所有商品很小一部分,大多数商品是不热门的甚至是冷门的).
(2) 仅仅基于用户行为数据设计的推荐算法一般称为协同过滤算法.可以细分为基于用户的协同过滤算法(给用户推荐和他兴趣相似用户感兴趣的商品)以及基于物品的协同过滤算法(给用户推荐其之间喜欢过的商品类似的商品)
2.3 基于领域的算法
(a) 基于用户的协同过滤算法
关键步骤:
1. 找到和目标用户兴趣相似的用户集合.给定用户u,v,我们定义N(u)为用户u有过正反馈的物品集合,同理定义N(v),利用jaccard公式计算u,v之间的相似度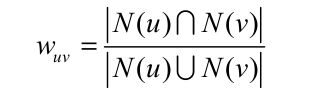
.可以用余弦公式
.
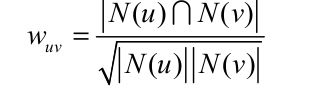2. 找到这个集合中用户喜欢,且目标用户没有接触过的物品推荐给目标用户.得到用户之间的兴趣相似度后, UserCF 算法会给用户推荐和他兴趣最相似的 K 个用户喜欢的物品。如下的公式度量了 UserCF 算法中用户 u 对物品 i 的感兴趣程度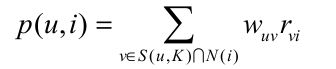
其中, S(u, K) 包含和用户 u 兴趣最接近的 K 个用户, N(i) 是对物品 i 有过行为的用户集合, $W_{uv}$表示用户 u 和用户 v 的兴趣相似度, $r_{vi}$ 代表用户 v 对物品 i 的兴趣.
对计算用户相似度的一个优化--两个用户对冷门物品采取过同样的行为更能说明他们的研究兴趣相同.改进后的用户兴趣相似度如下所示:
其中$\frac{1}{log1+\left|{N(i)}\right|}$惩罚了共同兴趣列表中热门物品对物品相似度的影响.
(b) 基础物品的协同过滤算法
网站的用户增加,计算用户相似度的时间复杂度以及空间复杂度的增长与用户数量的增长显平方的关系.基于用户的推荐系统算法很难对推荐的结果作出合理的解释.主要步骤分为一下两步:计算物品之间的相似度;根据物品的相似度和用户历史行为给用户生成推荐列表.
(1) 计算两个物品之间的相似度公式为: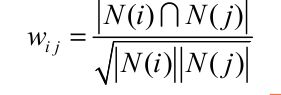 
,N(i)表示喜欢物品i的用户集合.公式可以理解为在喜欢i物品的用户中,有多少用户也喜欢物品j(基于用户的行为分析而不是基于商品的内容分析).分母中的|N(j)|用来惩罚物品j的热度,如果没有该惩罚项,那么一个热门的item会和很多物品都相似,这不是我们想要的效果.
(2) 得到item之间的相似度之后,itemCF通过如下公式计算用户u对一个物品j的兴趣: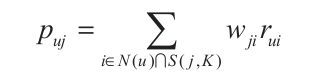
.这里N(u)是用户喜欢的物品的集合,S(j,K)是和物品j最相似的K个物品的集合,$w_{ij}$是物品j和i的相似度,$r_{ui}$是用户u对物品i的兴趣(兴趣通过反馈机制获取).
同uesrCF,这里对物品相似度也做一个修改,John S. Breese在论文中提出IUF ( Inverse User Frequence)参数,即用户活跃度对数的倒数,意义在于活跃用户对物品相似度的贡献应该小于不活跃的用户.公式如下:
(c) 物品相似度的归一化
归一化之后不仅可以增加推荐的准确度,还可以提高推荐的覆盖率和多样性.具体公式为: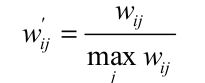
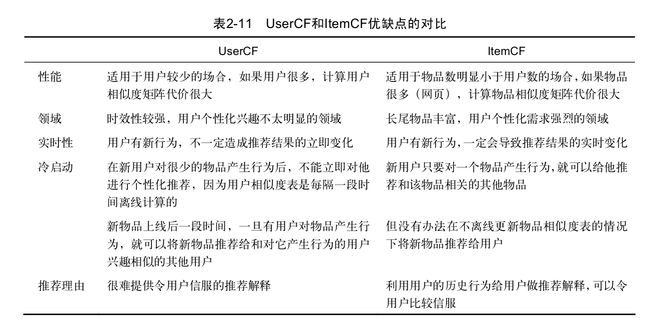
小结:UserCF和ItemCF的比较:
哈利波特问题
亚马逊网的研究人员在设计 ItemCF 算法之初发现 ItemCF 算法计算出的图书相关表存在一个问题,就是大部分图书都和<<哈利波特>>相似,想想之前计算itemCF的公式可以发现,出现这个问题是源于<<哈利波特>>这本书太热门了(即使分母有一定的惩罚项,还是会出现这样的问题).简单概括一下就是另个不同领域最热门物品之间往往具有比较高的相似度.要彻底解决这个问题需要引入物品的内容数据,这个不再协同过滤考虑的范畴之内了.
2.4 隐语义模型
除了itemCF以及userCF,还有按照兴趣分类的方法.对于如何分类?怎么确定用户对哪些物品感兴趣以及感兴趣的程度?对于一个给定的类,选择哪些属于这个类的物品推荐给用户,以及如何确定这些物品在一个类中的权重?是主要要解决的问题,上述三个问题都可以通过LFM(laten factor model)解决(这块的内容根据后续看论文的实际需求去补充吧).
核心思想为通过隐含特征联系用户以及用户兴趣和item.LFM 通过如下公式计算用户 u 对物品 i 的兴趣: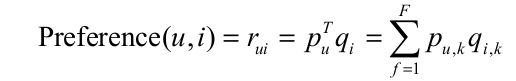
公式中$p_{u,k}$,$q_{i,k}$是模型的两个参数,其中$p_{u,k}$度量了用户u的兴趣和第k个隐类的关系,而$q_{i,k}$度量了第k个隐类和物品i之间的关系.对于计算这个两个参数,我们需要训练集,通过在训练集上进行训练来获得模型的参数.隐性反馈数据集上怎么获取负样本是一个难题.Rong Pan在其发表的论文中对比了以下四个法:
(a) 对于一个用户,用他所有没有过行为的物品作为负样本。
(b) 对于一个用户,从他没有过行为的物品中均匀采样出一些物品作为负样本.
(c) 对于一个用户,从他没有过行为的物品中采样出一些物品作为负样本,但采样时,保证每个用户的正负样本数目相当。
(d) 对于一个用户,从他没有过行为的物品中采样出一些物品作为负样本,但采样时,偏重采样不热门的物品。
(a)方法太随意了.效果是最差的.总体的效果为(c) > (b) > (d) > (a). 后续通过一些比赛总结出获取负样本的原则:对于每个用户,要保证正负样本的平衡(数目上相似);选取那些很热门而用户却没有行为的item.
经过采样可以得到一个用户—物品集 K = {( u , i )} ,其中如果(u, i)是正样本,则有 $r_{ui}=1$ ,否则有 $r_{ui}=0$.有了训练集之后,定义一个损失函数: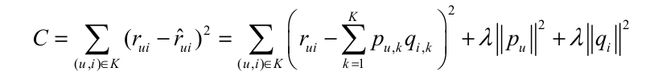
LFM和基于邻域方法的比较:
(1) 理论基础 LFM有个较好的机器学习理论方法,比较完善.
(2) 离线计算的空间复杂度 假设有M个用户以及N个物品,对于itemCF以及userCF空间复杂度为O(m*n)(关系矩阵的存在);对于LFM,假设有F个隐类,那么时间复杂度为O(F*(m+n)).LFM空间复杂度远优于基于领域的方法.
(3) 离线计算时间复杂度 假设有 M 个用户、 N 个物品、 K 条用户对物品的行为记录.UserCF 计算用户相关表的时间复杂度是 O(N * (K/N)^2)(在计算$w_{ij}$的过程中,对于每个物品平均有k/n个用户有过行为.在计算c[i][j]的时候遍历N个物品,然后对于每个物品对有过用户行为的用户计数需要O((K/N)^2)).而对于 LFM ,如果用 F 个隐类,迭代 S 次,那么它的计算复杂度是 O(K * F * S).如果 K/N > F*S ,则代表 UserCF 的时间复杂度低于 LFM.
(4) 在线实时推荐 LFM通过机器学习训练的方式获取喜好矩阵A[i][j])(用户i对物品j的喜好程度),每次加入新的物品之后需要再次训练,然后排序取前k个值.时间复杂度过大,不适合直接用于在线的实时推荐. (关于itemCF为什么可以用来实时推荐 这里后面补一下 暂时不是很清楚)
(5) 推荐解释性质 itemCF有着不错的推荐解释性质,LFM则没有.
2.5 基于图的模型
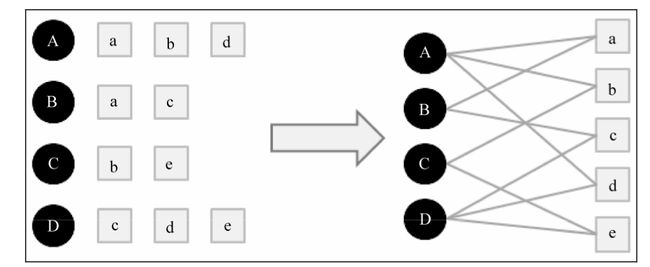
用户行为很容易用二分图表示.令 G ( V , E )表示用户物品二分图,其中 V由用户顶点集合 $V_U$和物品顶点集合 $V_I$组成,对于数据集每一个二元组(u,i)(表示为用户u对item i有行为)可以用边$e(v_u,v_i)$表示,简单的二分图如下所示:
(a) 基于图的推荐算法
在二分图上进行个性化推荐,那么给用户 u 推荐物品的任务就可以转化为度量用户顶点$v_u$和与$v_u$没有边直接相连的物品节点在图上的相关性,相关性越高的物品在推荐列表中的权重就越高.
图中顶点的相关性主要取决于三点:
> 两个顶点之间的路径数
> 两个顶点路径的长度
> 两个顶点之间的路径经过的顶点
相关性高的一对顶点一般有如下特征:
> 两个顶点之间有很多路径可以相连
> 连接两个顶点之间的路径长度都比较短
> 连接两个顶点之间的路径不会经过出度比较大的点
PersonalRank算法
定义PR(i)为节点i的重要性,假设要给用户 u 进行个性化推荐,可以从用户 u 对应的节点 $v_u$开始在用户物品二分图上进行随机游走(PR(i) = 0 ,其余节点PR值为0)。游走到任何一个节点时,首先按照概率 α 决定是继续游走,还是停止这次游走并从 $v_u$节点开始重新游走。如果决定继续游走,那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点b,相应的PR(b)要加上α *PR(a)/|a的出度数|。如果选择停在该点,那么该点的PR(u)要加上(1-α)PR(u)。重复上述过程直到PR值收敛。描述为公式可表示为
其中in(v)表示节点v入边对应的节点集合(除去v本身),out(v)表示节点v的出边对应的节点集合(除去v本身)。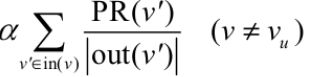
表示从$v^,$转移过来,第二步表示停留在该节点.(个人理解PersonalRank算法通过给定起点的初始值,然后在随机游走的过程中不断的把值按一定规则传给和其相连的节点,这里每次传播值都是减少的.当游走收敛时,节点的值就可以作为该节点和起点之间联系的一个判断值)
PersonalRank 算法迭代的时间复杂度过高,不适合实时的推荐.相应的解决方法有两类,一类是减少迭代次数(牺牲精度),另一类是从矩阵论出发,重新设计算法.