集聚系数global / local Clustering coefficient
Clustering coefficient的定义有两种:全局的和局部的。
triplet是一个三元组=三个节点,其中三个节点有2条边=open triplet 三个节点加3条边=closed
全局集聚系数=closed/(open+closed)
全局的算法基于triplet。triplet分为开放的triplet(open triplet)和封闭的triplet(closed triplet)两种(A triplet is three nodes that are connected by either two (open triplet) or three (closed triplet) undirected ties)。
可以用下面结构定义一个triplet
struct triplet { int key; set pair;};
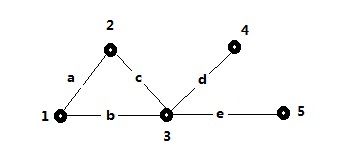
例如下图{1,(2,3)}构成的triplet是封闭的,{3,(4,5)}构成的triplet是开放的
全局的Clustering coefficient比较简单,公式如下:Clustering coefficient(global) = number of closed triplet / number of triplet(closed+open)
以上图为例:
closed triplet ={1,(2,3)},{2,(1,3)},{3,(1,2)}
all triplet = {1,(2,3)},{2,(1,3)},{3,(1,2)},{3,(2,4)},{3,(4,5)},{3,(1,5)},{3,(2,5)},{3,(1,4)}
number of closed triplet = 3
number of triplet = 8
number of triplet / number of triplet = 3/8=0.375
局部的Clustering coefficient的计算方法:
计算当前节点的所有邻居之间的实际连边数/可能有的所有连接数
局部计算是面向节点的,对于节点vi,找出其直接邻居节点集合Ni,计算Ni构成的网络中的边数K,除以Ni集合可能的边数|Ni|(|Ni|-1)/2
例如:
1节点的邻居节点(2,3),他们之间构成的边有1条,可能构成的边1条,因此1/1=1
2节点的邻居节点(1,3),他们之间构成的边有1条,可能构成的边1条,因此1/1=1
3节点的邻居节点(1,2,4,5),他们之间构成的边有1条,可能构成的边(43)/2条,因此1/6=1/6
4节点的邻居节点(3),他们之间构成的边有0条,可能构成的边0条,因此0
5节点的邻居节点(3),他们之间构成的边有0条,可能构成的边0条,因此0
则,5个节点平均local Clustering coefficient = (1+1+1/6)/5=13/30=0.4333
python中的networkx自带的函数,计算的是平均集聚系数,也就是local
# -*- coding: utf-8 -*-
"""
Created on Wed Feb 5 09:57:14 2020
@author: LYN
"""
import numpy as np
import networkx as nx
Gmatrix=np.array([[0,1,1,0,0],[1,0,1,0,0],[1,1,0,1,1],[0,0,1,0,0],[0,0,1,0,0]])
G = nx.from_numpy_matrix(Gmatrix)
c=nx.average_clustering(G)
In[7]: c
Out[7]: 0.4333333333333333
参考
1)https://www.cnblogs.com/startover/p/3141646.html
2)http://blog.csdn.net/pennyliang/article/details/6838956