论文笔记 Reinforced Feature Points: Optimizing Feature Detection and Description for a High-Level Task
代码解读
介绍
\quad 文章的主要思路是使用SuperPint的预训练模型,使用旋转矩阵 R R R和平移矩阵 t t t对SuperPoint进行reinforcement learning, 使其能够估计相机的相对位姿变化。
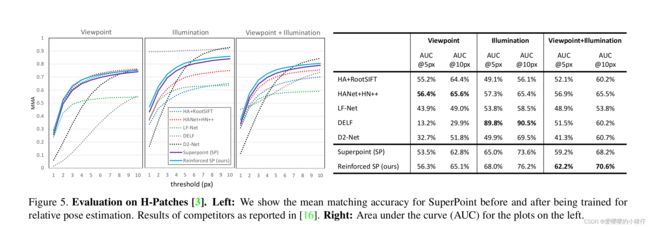
作者指出对神经网络的训练,SuperPoint在匹配任务上取得了比SIFT更好的效果,但其在根据匹配求解本质矩阵上,效果却不如SIFT,同为深度学习网络的LIFT也存在相同的问题,LIFT特征在三维重建任务中的效果不如SIFT,基于深度学习方法的特征点在底层任务(如匹配)中取得很好效果的同时,在高层任务(如视觉重定位、sfm、SLAM)中的效果却不尽如人意。本文中作者希望通过一个训练pipeline,使得深度学习特征在高层任务中用可以获得很好的效果,本文采用的训练方式是最小化相机的位姿误差(即相机真实位姿变换和根据匹配求解的位姿之间的差值)。
方法描述
\quad 主要目的是求解变化矩阵 T = ( R , t ) T=(R,t) T=(R,t),其中 R R R是旋转矩阵, t t t是平移矩阵。记两张待匹配的图像分别为 I I I和 I ′ I' I′,第 i i i个2D特征点为 x i x_i xi,其对应的描述子为 d ( x i ) d(x_i) d(xi)。通过对所求出的描述子做最近邻匹配,得到 I I I和 I ′ I' I′之间的暂定匹配对 m i j = ( x i , x j ′ ) m_{ij}=(x_i,x_j') mij=(xi,xj′)。然后使用这些匹配,通过五点法求解本质矩阵,如果该点通过本质矩阵求得的对应点距离极线的距离小于阈值,则认为该点为内点(相当于用对极约束进行判断),选择使内点数最多的本质矩阵作为待使用的本质矩阵 E E E,然后求得两帧之间的位姿变换矩阵 T ^ \hat{T} T^。
\quad 文本采用了SuperPoint,这是一个可以同时训练特征检测器(产生关键点)和描述器(产生描述子)的网络架构。关键点和选取以及特征的匹配是离散、不可微分的操作,因此不能像传统的监督训练一样,将求得的变换矩阵 T ^ \hat{T} T^反传回来更新网络权重。作者同时指出RANSAC等估计也不是可微的。因此,使用了强化学习的思路来设计损失函数。我们将特征的检测和匹配当成概率事件,假定该事件取决于神经网络的输出。在训练过程中,我们基于神经网络预测的概率分布,采样不同的关键点和匹配实例。我们观察这些特征点和匹配在视觉任务中表现如何,从而调整神经网络的参数,使得网络的输出有尽可能小的损失。
提点
\quad 记特征提取网络针对图片 I I I预测出的heat map为 f ( I ; w ) f(I;w) f(I;w)。特征的具体位置通常选在heat map上局部最大值点,并且通常会用非极大值抑制(NMS)的方法以避免点的过度聚集。为了使得特征点的选取概率化,我们则采用概率分布的思路预测heat map,从而求解特征点的位置 f ( I ; w ) = P ( x ; w ) f(I;w)=P(x;w) f(I;w)=P(x;w)。记图像 I I I的 N N N个特征点集合为 X = { x i } \mathcal{X}=\{{x_i}\} X={xi},假设每个特征是否被选取相互独立,则
P X ; w = ∏ i = 1 N P ( x i ; w ) P{\mathcal{X};w}=\prod^N_{i=1}P(x_i;w) PX;w=i=1∏NP(xi;w)
对于图片 I I I,满足同样的假设,记图像 I ‘ ’ I‘’ I‘’的 N N N个特征点集合为 X ‘ ’ \mathcal{X‘’} X‘’,两张图片上特征点的联合概率分布可以记为:
P ( X ; X ′ ; w ) = P ( X ; w ) P ( X ′ ; w ) P(\mathcal{X};\mathcal{X'};w)=P(\mathcal{X};w)P(\mathcal{X'};w) P(X;X′;w)=P(X;w)P(X′;w)
具体示意可以参照图2左下角。
特征匹配
\quad 记关键点 x x x对应的描述子为 d ( x ; w ) d(x;w) d(x;w),为了记号的简介性,这里用 w w w来代表通过特征提取和匹配学习来的参数,记图片 I I I和 I ′ I' I′的一组关键点匹配为 m i j = ( x i , x j ′ ) m_{ij}=(x_i,x_j') mij=(xi,xj′),这里给出 x i x_i xi和 x j ′ x_j' xj′可以成功匹配上的概率估计:
P ( m i j ∣ X , X ′ ; w ) = e x p [ − ∣ ∣ d ( x i ; w ) − d ( x j ′ ; w ) ∣ ∣ ] ∑ m k k ′ e x p [ − ∣ ∣ d ( x k ; w ) − d ( x k ′ ; w ) ∣ ∣ ] P(m_{ij}|\mathcal{X},\mathcal{X'};w)=\frac{exp[-||d(x_i;w)-d(x_j';w)||]}{\sum_{m_{kk'}}exp[-||d(x_k;w)-d(x_k';w)||]} P(mij∣X,X′;w)=∑mkk′exp[−∣∣d(xk;w)−d(xk′;w)∣∣]exp[−∣∣d(xi;w)−d(xj′;w)∣∣]
该分部使用所有可能的匹配对 m k k ′ = ( x k , x k ′ ) ( 其 中 , x k ∈ X , x k ′ ′ ∈ X ′ ) m_{kk'}=(x_k,x_k')(其中,x_k\in \mathcal{X},x'_{k'} \in \mathcal{X'}) mkk′=(xk,xk′)(其中,xk∈X,xk′′∈X′)进行归一化。从上式可以得知,越类似的描述子匹配上的概率越高,相对未匹配的描述子,网络会减少匹配描述子之间的距离。记 m i j m_{ij} mij的集合为 M \mathcal{M} M,关于 M \mathcal{M} M的概率分布可以写成:
P ( M ∣ X , X ′ ; w ) = ∏ m i j ∈ M P ( m i j ∣ X , X ′ ; w ) P(\mathcal{M}|\mathcal{X},\mathcal{X'};w)=\prod_{m_{ij} \in \mathcal{M}}P(m_{ij}|\mathcal{X},\mathcal{X'};w) P(M∣X,X′;w)=mij∈M∏P(mij∣X,X′;w)
学习策略
\quad 我们学习网络的参数 w w w通过监督的方式,假定训练的数据形式是 ( I , I ′ , T ∗ ) (I,I',T^*) (I,I′,T∗),其中 T ∗ T^* T∗是变换矩阵的真值。这里注意并没有用到关键点位置 X \mathcal{X} X和图像匹配 M \mathcal{M} M的真值。
\quad 我们将特征匹配之后的处理过程设计成黑盒模型,该模型只有一个输出,损失值 ℓ ( M , X , X ′ ) \ell(\mathcal{M},\mathcal{X},\mathcal{X'}) ℓ(M,X,X′),该值取决于挑选出来的特征点 X \mathcal{X} X和 X ′ \mathcal{X'} X′,以及挑选出来的匹配 M \mathcal{M} M。减少 ℓ \ell ℓ使得其尽可能求得两张图像对应的真实的本质矩阵,进而求得相机的相对位姿变换矩阵 T ^ \hat{T} T^, ℓ \ell ℓ的本质就是 T ∗ T^* T∗和 T ^ \hat{T} T^的差。我们只需要损失自身,而不需要损失的梯度。
w w w的概率分布可以写成:
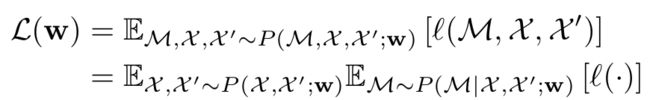
这里简记 ℓ ( M , X , X ′ ) \ell(\mathcal{M},\mathcal{X},\mathcal{X'}) ℓ(M,X,X′)为 ℓ ( ⋅ ) \ell(\cdot) ℓ(⋅)。我们将该期望分解为了特征提取和匹配两部分的乘积。为了避免特征过多,匹配计算量过大,我们使用SuperPoint的预训练模型,这样提取的特征大部分是有效的,可以有效减少无效匹配的计算时间。但这种做法有两个性质:1、特征检测器预测出来的heat map是稀疏的,相对于全体像素,将关键点挑选出来的概率几乎为0。2、不相关特征之间描述子距离很大,对期望几乎不产生影响。
性质1意味着我们可以直接从关键点的heat map中采样,忽略图像的其他位置,性质2表明对于选定的 X \mathcal{X} X中的关键点,我们没有必要用 X ′ \mathcal{X'} X′中每一个关键点与其匹配,可以使用k近邻匹配的策略。
\quad 我们使用上式的梯度来更新参数 w w w:
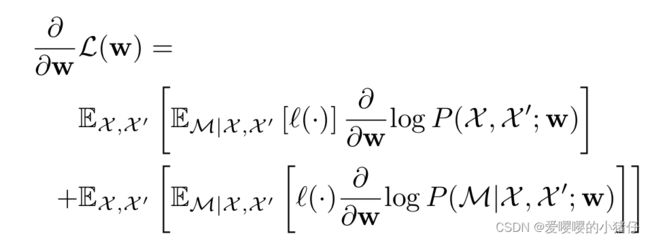
\quad 这里我们只需要计算关键点提取以及特征匹配指数概率的梯度。我们通过采样近似了梯度计算的期望。