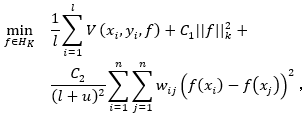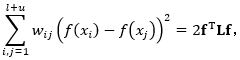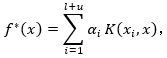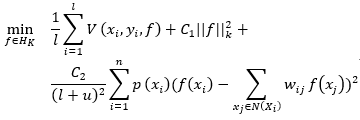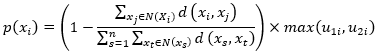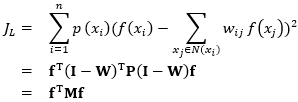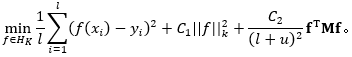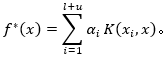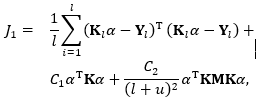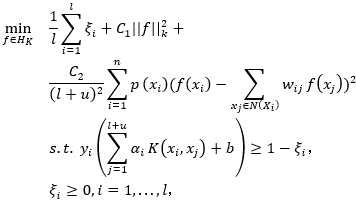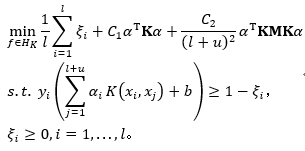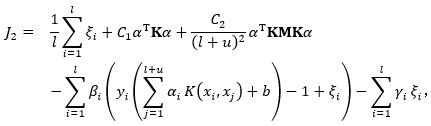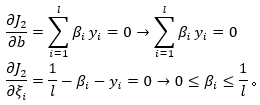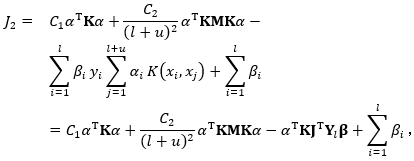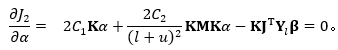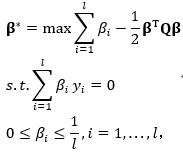逐点流行正则化方法及其在半监督学习上的应用

0、前言        

       在许多实际应用中，未标记的数据可以很容易和廉价地收集，而获取有标记的数据通常是相当昂贵和耗时的，特别是涉及人工工作。半监督学习尝试利用未标记数据所披露的内在数据分布信息，以提升学习效果，引起了广泛的关注。流形正则化是半监督学习常用方法之一。流形正则化通常将每个实例对视为对象，并约束流形图上的相似实例对应该具有相似的分类输出，因此，它是建立在流形图上的成对平滑性之上的。然而，平滑约束在自然界中可以是点态的（即点态平滑），平滑不应该局限于成对平滑。点态平滑将每个点的行为与其近邻的行为联系起来，实际上，基于聚类假设的半监督学习方法通常会实现点态平滑。已有研究者尝试将点态平滑引入流形正则化，提出了一种基于点态平滑的流形正则化方法：逐点流形正则化方法(PW_MR)。本博文介绍PW_MR相关理论，及其在半监督学习中的应用。

1、基于成对平滑性的流形正则化框架（MR）

        流形假设是半监督学习中最常用的数据分布假设之一，它假设在流形结构上的相似实例应该共享相似的分类输出。基于流形假设，流形正则化(MR)近年来已被深入研究且已被应用在不同的领域。

        那么给定一个数据集，已标记数据定义为：

与之相对应的标签：

未标记的数据定义为：

其中每个样本：

且

 该流形图在整个数据集上的构造为：

其中权重表示所连接实例对之间的相似性。基于这样的流形图，基于MR的半监督学习框架表述如下：

 其中：f(x)为决策函数，C1和C2均为正则化参数，是损失函数，例如最小二乘分类器的平方损失（RLSC）：

是在再生核希尔伯特空间（ Reproducing Kernel Hilbert Space）中保证平滑性的一个正则项。第三项则保证了流形图上的点对之间的光滑性，即相似的实例应该在流形结构上共享相似的分类输出。它可以进一步写成：

其中：

L是由L=D-W给出的图拉普拉斯矩阵，W是图G的权重矩阵，D是由组成的对角矩阵 。

 由表示定理（Representer theorem），决策函数有如下形式：

 其中：是一个核函数（Mercer kernel）。

2、基于点态平滑性的流形正则化半监督学习框架（PW_MR)

        流形学习对实例对采用正则化项，以约束流形图上的相似实例对共享相似的分类输出，从而实际实现了点对之间的平滑性。在本节中，作者介绍了一个依据点态平滑度的逐点流形学习框架。通过逐点实现平滑性约束，可以将基于PW_MR的半监督学习框架表述为:

 其中:表示的领域集；表示每个实例周围的局部密度，它可以根据实例与其近邻之间的归一化距离来计算，值越小表示实例周围的分布越密集。但是，当一个实例在类的重叠区域时，那么根据上述的局部密度，周围局部密度将变得很大。因此，在上式的第三项中将受到更重视或更大的处罚，但显然这是意料之中的。因此，在计算局部密度时，应该同时考虑了邻居密度和无监督学习结构，即：

 式中：表示实例与其邻居之间的距离，描述了集群成员关系，或者在某个无监督学习方法如FCM中，属于单个集群的概率。的第一部分考虑每个实例与其近邻之间的归一化距离，值越小表示周围的分布越密集，因此的值越大，最后在上式中的惩罚越大；第二部分考虑了无监督学习方法的结果，因为无监督学习方法通常可以用来检测分布结构的内在边界，的值越大，表示成为非边界实例的概率越大 。

        对比MR半监督学习框架与PW_MR半监督学习框架：MR学习框架的第三项是对实例对有平滑惩罚的正则项（即考虑成对平滑性）；PW_MR学习框架中的第三项考虑了在单个实例上的平滑性（即考虑了点态平滑性），PW_MR通过考虑局部密度来引入每个实例的重要性。我们可以在PW_MR学习框架中进一步重写第三项为：

 其中，W是邻域相似度矩阵，组成元素表示如下：

是一个单位矩阵；是一个对角矩阵且对角分量。

3、PW_MR在半监督学习中的应用

3.1 逐点流形正则最小二乘法

        将PW_MR学习框架与最小二乘法结合，形成具有半监督学习能力的逐点流形正则最小二乘法（PW_LapRlsc）。即PW_MR框架中，我们采用的是平方损失函数。

PW_LapRlsc框架可以表述为：

 同理，在应用了表示定理（Representer theorem）后，转换为如下形式

 因此，最优化函数为：

 由此可以得出：

3.2 逐点流形正则支持向量机（PW_LapSVM）

        同理，将PW_MR学习框架与支持向量机SV，形成具有半监督学习能力的逐点流形正则支持向量机（PW_LapSVM）方法。

        PW_LapSVM框架可以表述为：

基于前述推导，求解公式可以表示为以下形式：

  在应用了拉格朗日乘子法进行优化后，可以得到下式：

 为拉格朗日乘参数；对上述函数求导：

进一步推算：

 其中是一个的矩阵，其中为为单位矩阵,且 

进而：

因此：

将其替换回上式，简化拉格朗日量，可以得到：

其中：

4、总结

        上述描述了 PW_MR学习框架与最小二乘法、SVM的结合，实际上PW_MR学习框架还可以和其他算法结合，例如：与极限学习结合形成逐点流形正则极限学习机（PW_LapELM）。

        思维拓展：PW_MR学习框架只能用于分类吗？答案肯定是：否。完全可以用于回归预测（逐点流形正则最小二乘法就可以用来回归预测啊！)；甚至还可以用来做特征提取（将框架中决策函数理解为特征转换方式呗！损失函数替换为信息损失呗，如方差、信息熵...）；甚至还可以和神经网络的训练结合，将其纳入神经网络的目标函数，引导神经网络能提取到更好的特征。。。。。