数据结构与算法:12种排序全代码
排序
文章目录
- 排序
-
- 1.冒泡排序
-
- 思路:
- 优化:
- 交换过程:
- C语言代码:
- 优化后:
- 2.直接插入排序
-
- 思路:
- 过程:
- 代码:
- 3.折半插入排序
-
- 折半查找
- 代码
- 4.希尔插入排序
-
- 思路:
- 排序过程:
- 代码
- 5.选择排序
-
- 思路:
- 排序过程:
- 代码
- 6.鸡尾酒排序法
-
- 思路:
- 代码
- 7.堆排序
-
- 思路:
- 代码
- 8.归并排序
-
- 思路:
- 代码
- 9.快速排序
-
- 思路:
- 代码
- 10.计数排序
-
- 思想:
- 代码
- 11.桶排序
-
- 思路:
- 代码
- 12.基数排序
-
- 思路
- 过程:
- 代码
- 代码
各种排序算法的时间复杂度和空间复杂度
排序算法比较表格
排序算法 平均时间复杂度 最坏时间复杂度 空间复杂度 是否稳定
冒泡排序 O(n2)O(n2) O(n2)O(n2) O(1)O(1) 是
选择排序 O(n2)O(n2) O(n2)O(n2) O(1)O(1) 不是
直接插入排序 O(n2)O(n2) O(n2)O(n2) O(1)O(1) 是
归并排序 O(nlogn)O(nlogn) O(nlogn)O(nlogn) O(n)O(n) 是
快速排序 O(nlogn)O(nlogn) O(n2)O(n2) O(logn)O(logn) 不是
堆排序 O(nlogn)O(nlogn) O(nlogn)O(nlogn) O(1)O(1) 不是
希尔排序 O(nlogn)O(nlogn) O(ns)O(ns) O(1)O(1) 不是
计数排序 O(n+k)O(n+k) O(n+k)O(n+k) O(n+k)O(n+k) 是
基数排序 O(N∗M)O(N∗M) O(N∗M)O(N∗M) O(M)O(M) 是
1.冒泡排序
| 时间复杂度 | O(n²) |
|---|---|
| 算法稳定性 | 稳定排序算法 |
| 实 质 | 把小(大)的元素往前(后)调 |
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
思路:
1、任何两个相邻的数进行比较 大的放后面 小的放前面
2、如果对数组中的元素进行一次遍历(即从下标为1开始,到数组最后一个元素,每个元素和其前面一个元素比较,大的放后面,小的放前面)经过这样一次遍历之后,最大的元素已经到达最末尾
3、针对所有的元素重复以上的步骤,除了最后一个。第二次遍历 从下标为1开始 到小于 n-1 下标位置
第三次遍历 从下标为1开始 到小于 n-2 下标位置
如果有n个元素,重复n-1遍上面的遍历即可完成排序
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
优化:
当进行一次完整的遍历 没有任何两个数发生交换时数组已经有序
交换过程:
8 6 1 5 4 3 9 0 2 7
i
6 8 1 5 4 3 9 0 2 7
i
6 1 8 5 4 3 9 0 2 7
i
6 1 5 8 4 3 9 0 2 7
i
6 1 5 4 8 3 9 0 2 7
i
6 1 5 4 3 8 9 0 2 7
i
6 1 5 4 3 8 9 0 2 7
i
6 1 5 4 3 8 0 9 2 7
i
6 1 5 4 3 8 0 2 9 7
i
6 1 5 4 3 8 0 2 7 9
1 5 4 3 6 0 2 7 8 9
1 4 3 5 0 2 6 7 8 9
1 3 4 0 2 5 6 7 8 9
1 3 0 2 4 5 6 7 8 9
1 0 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
C语言代码:
#include
void swap(int *pa,int *pb){
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
void bubble(int arr[],int len){
int i,j;
for(i=0;i 优化后:
//冒泡
void bubble_sort(int arr[],size_t n){
size_t i,j;
for(i=1;iarr[j]){
swap(&arr[j-1],&arr[j]);
hasSwap = true;
}
}
if(!hasSwap){
break;
}
}
}
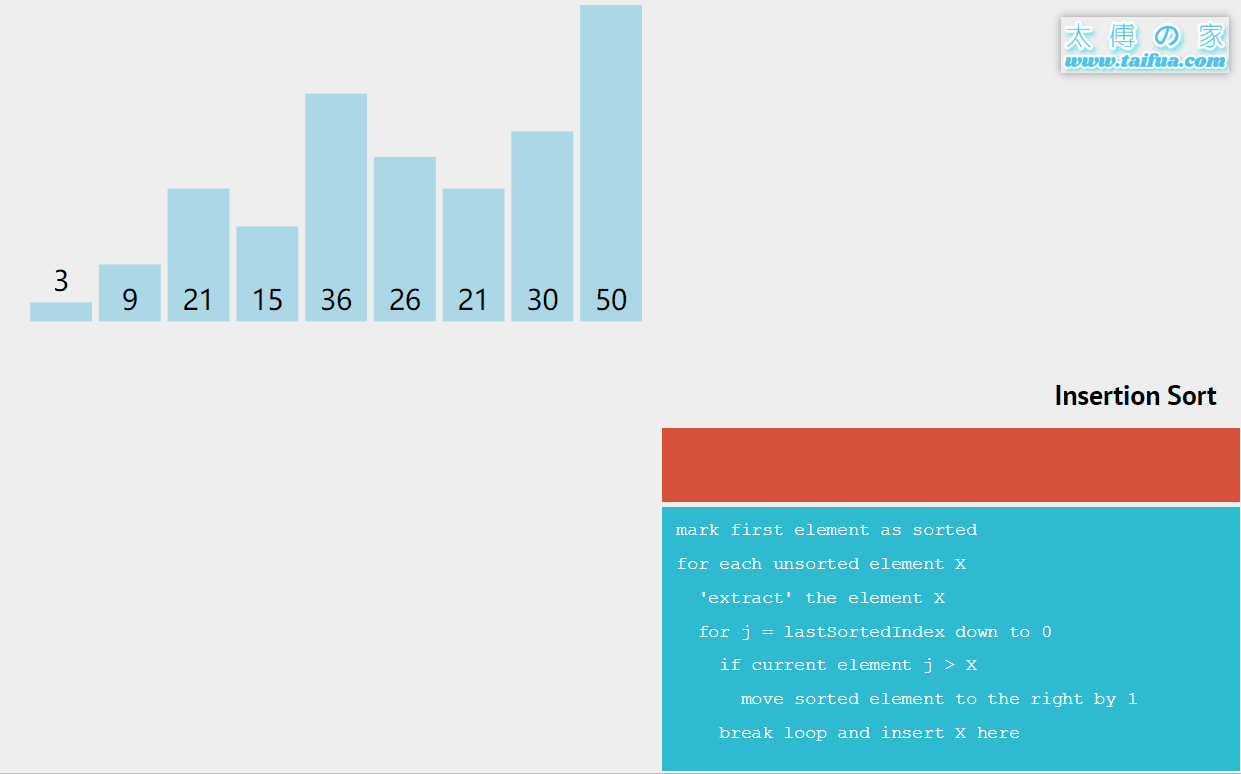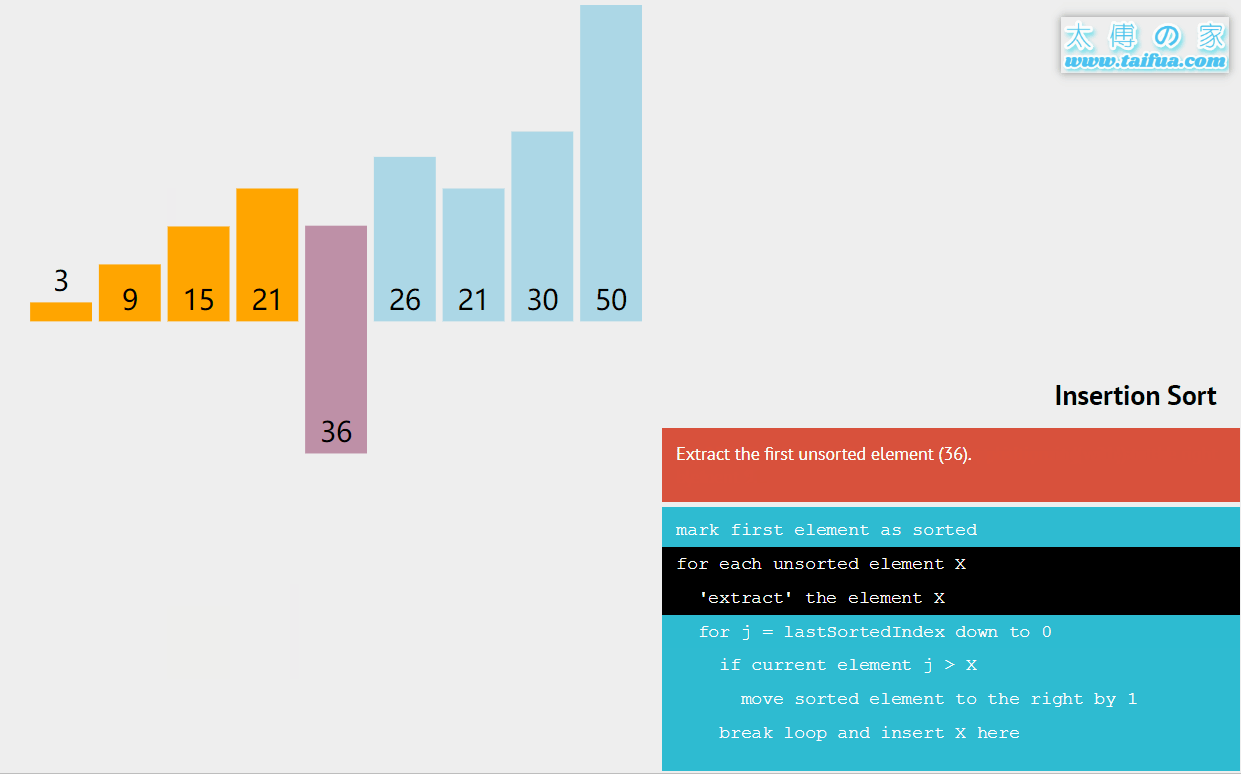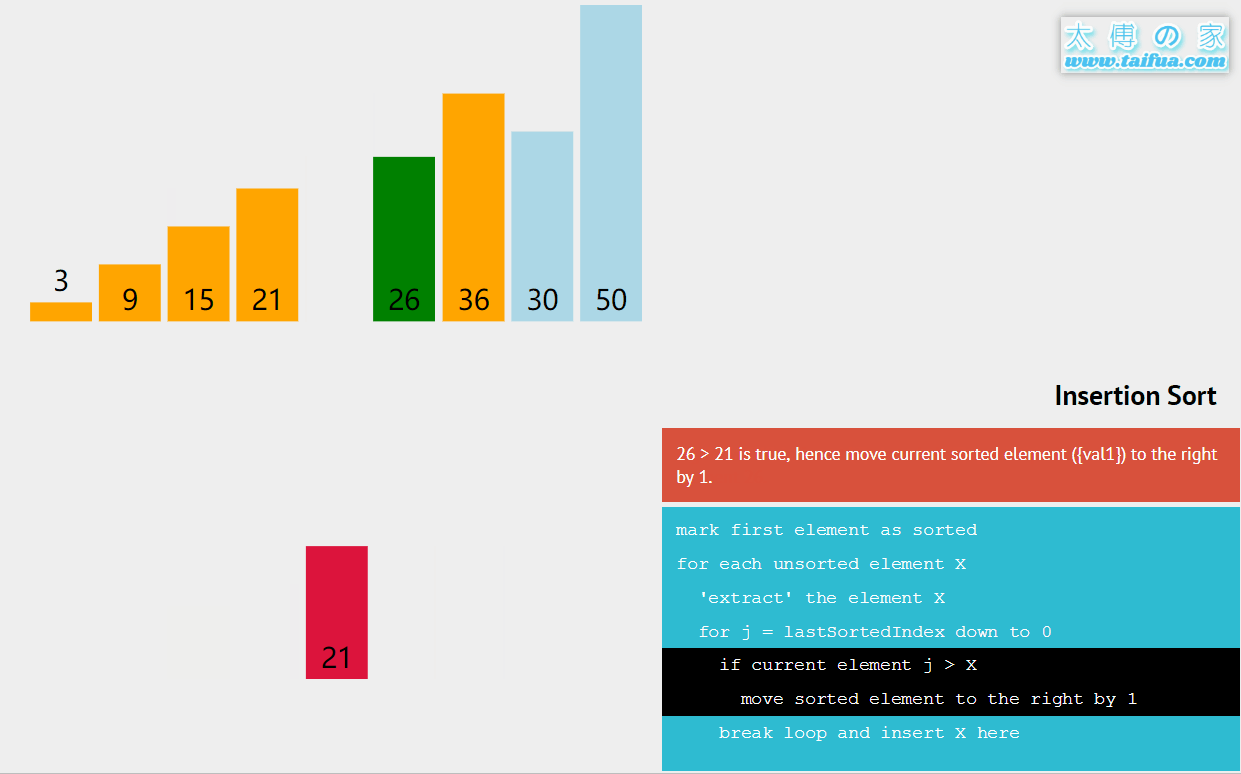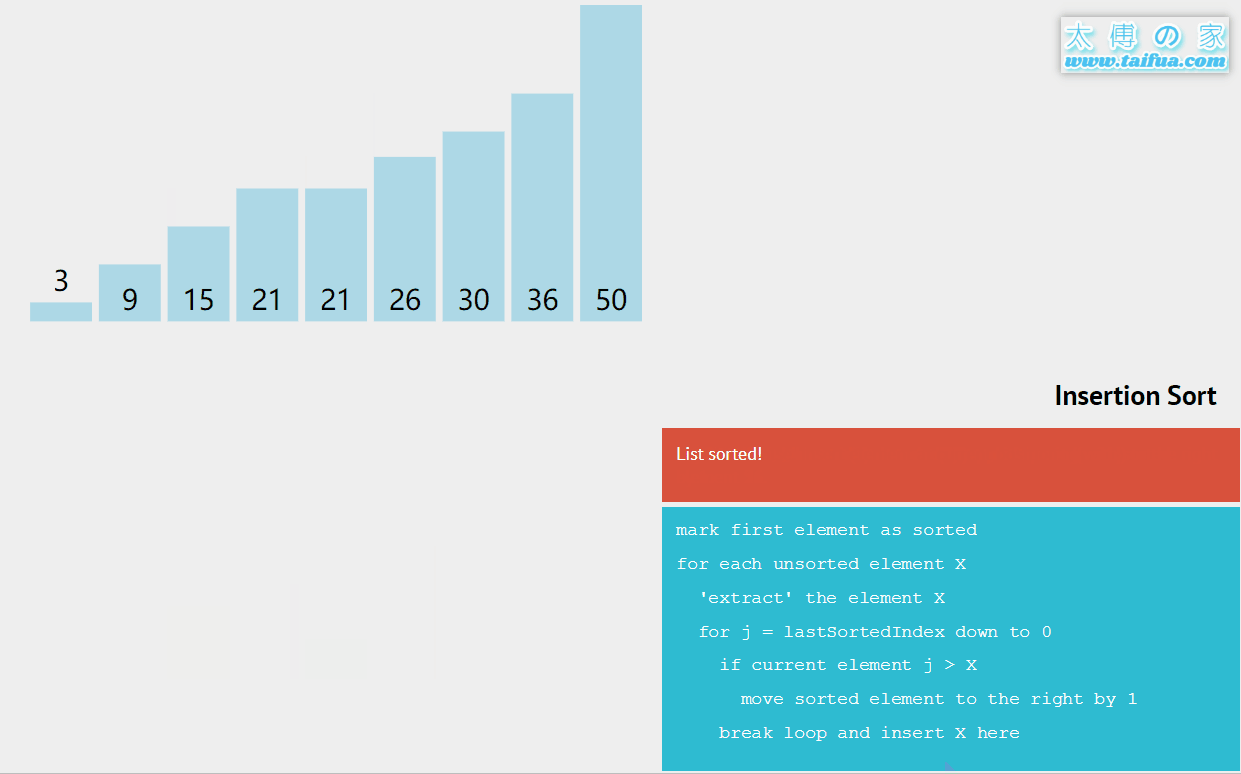
2.直接插入排序
| 时间复杂度 | O(n^2) |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 稳定 |
直接插入排序(Straight Insertion Sort)是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的、记录数量增1的有序表。
思路:
把一个数插入到一个有序的数列中
把数组中的元素逐个插入到一个有序的数列当中
从数组中的第一个元素开始,把这个元素记录为key
把key插入到前面有序的数组中
假设下标为i的元素记录为key,把key插入到arr[0]—arr[i-1]这个数组中使之保持有序
j从i-1开始遍历,如果arr[j]大于key,那么arr[j]往后移一个位置,直到j小于0或者arr[j]比key小 则arr[j+1]的位置放置key元素
过程:
8 6 1 5 4 3 9 0 2 7
i
key = 6
6 8 1 5 4 3 9 0 2 7
i
key = 1
1 6 8 5 4 3 9 0 2 7
i
key = 5
1 5 6 8 4 3 9 0 2 7
i
key = 4
1 4 5 6 8 3 9 0 2 7
i
key = arr[i]; key = 3;
j
j>=0&&arr[j]>key
arr[j+1] = arr[j] --j
1 3 4 5 6 8 9 0 2 7
int key = arr[i];
key插入到 arr[0]-- arr[i-1] 这个有序数组中
代码:
void insert_sort(int arr[],size_t n){
int i,j;
for(i=1;i=0 && arr[j]>key;j--){
arr[j+1] = arr[j];
}
arr[j+1] = key;
}
}
3.折半插入排序
| 时间复杂度 | O(n^2) |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 稳定 |
折半查找
是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中,比直接插入算法明显减少了关键字之间比较的次数。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
代码
void bin_insert_sort(int arr[],size_t n){
int i,j;
for(i=1;i=left;j--){
arr[j+1] = arr[j];
}
arr[left] = key;
}
4.希尔插入排序
| 时间复杂度 | O(n^(1.3—2)) |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
插入排序的优化
避免像直接插入时大量地移动一个数据 把一个数据放到大致的位置
思路:
本质也是插入,实质上是一种分组插入方法
先分组 组内进行插入排序 每次组减小
排序过程:
step = 10/2 10个数 分为5组
8 6 1 5 4 3 9 0 2 7
对每一个分组进行插入排序
arr[0] arr[5] 3 6 1 5 4 8 9 0 2 7
arr[1] arr[6] 3 6 1 5 4 8 9 0 2 7
arr[2] arr[7] 3 6 0 5 4 8 9 1 2 7
arr[3] arr[8] 3 6 0 2 4 8 9 1 5 7
arr[4] arr[9] 3 6 0 2 4 8 9 1 5 7
step = step/2 2
arr[0] arr[2] arr[4] arr[6] arr[8]
3 6 0 2 4 8 9 1 5 7
0 6 3 2 4 8 9 1 5 7
0 6 3 2 4 8 5 1 9 7
arr[1] arr[3] arr[5] arr[7] arr[9]
0 6 3 2 4 8 5 1 9 7
0 2 3 6 4 8 5 1 9 7
0 1 3 2 4 6 5 8 9 7
0 1 3 2 4 6 5 7 9 8
step = step/2 1
0 1 3 2 4 6 5 7 9 8
0 1 2 3 4 5 6 7 8 9
代码
//希尔排序
void shell_sort(int arr[],size_t n){
size_t step;
//分组
for(step = n/2;step > 0; step = step/2){//step步长
size_t i;
//除了每组第一个元素以外 组内每个元素相隔step
//对于后面所有的元素都要进行组内插入排序
for(i=step;i=0 && arr[j]>key;j=j-step){//和组内元素比较
arr[j+step] = arr[j];
}
arr[j+step] = key;
}
}
}
5.选择排序
| 时间复杂度 | O(n^2) |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
思路:
每次在一个区间内找到最大值(记录下标) 把最大值和最末尾元素交换
改变区间重复上面的步骤 即可完成排序
完整遍历一次数组 能找到最大值 (记录下标位置)
把最大值 和 末尾元素交换
不考虑最后一个元素的情况下 遍历一次数组 找到一个最大值
把最大值 和 倒数第二个元素交换位置
存在的问题:在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序是一个不稳定的排序算法。
排序过程:
8 6 1 5 4 3 9 0 2 7
8 6 1 5 4 3 7 0 2 9
2 6 1 5 4 3 7 0 8
2 6 1 5 4 3 0 7
2 0 1 5 4 3 6
2 0 1 3 4 5
2 0 1 3 4
2 0 1 3
1 0 2
0 1
代码
void choice_sort(int arr[],size_t n){
size_t i,j;
for(i=0;iarr[m]){
m = j;
}
}
if(n-i-1 != m){
swap(&arr[n-1-i],&arr[m]);
}
}
}
6.鸡尾酒排序法
| 时间复杂度 | O(n^2) |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 稳定 |
数组中的数字本是无规律的排放,先找到最小的数字,把他放到第一位,然后找到最大的数字放到最后一位。然后再找到第二小的数字放到第二位,再找到第二大的数字放到倒数第二位。
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
思路:
遍历一次能记录最大值和最小值位置
把最大值放到区间末尾
把最小值放到区间开始位置
改变区间大小 左右发生变量
记录的是 下标位置
图解:https://blog.csdn.net/hujingshuang/article/details/48741207
代码
void cocktail_sort(int arr[],size_t n){
size_t i,j;
for(i=0;iarr[max]){
max = j;
}
if(arr[j] void cock_tail_sort(int arr[],size_t n){
size_t right=n-1,left=0;
int i = 0;
while(leftarr[i+1]){
swap(&arr[i],&arr[i+1]);
}
}
right--;
for(i=right;i>left;i--){
if(arr[i] 7.堆排序
| 时间复杂度 | |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
时间复杂度:
O ( n l o g 2 n ) {O(nlog_2{n})} O(nlog2n)
堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7k59kipA-1576213558173)(C:\Users\lenovo\OneDrive\指针信息\ps_ds\队列与堆排序.gif)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-W4qZE5kT-1576213558174)(C:\Users\lenovo\OneDrive\指针信息\ps_ds\03ds\堆排序.gif)]
思路:
把数组调整成大堆
把第一个元素和最后一个元素进行交换
不考虑最后一个元素 重新调整成大堆
重复上面的步骤
在堆的数据结构中,堆中的最大值总是位于根节点(在优先队列中使用堆的话堆中的最小值位于根节点)。堆中定义以下几种操作:
- 最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build Max Heap):将堆中的所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
代码
void reheap(int arr[],size_t index,size_t n){
size_t child = 2*index+1;
int key = arr[index];
while(child < n){
if(child+1 < n && arr[child]< arr[child+1]){
++child;
}
if(keyvoid max_heapify(int arr[], int start, int end)
{
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) //若子节点指标在范围内才做比较
{
if (son + 1 <= end && arr[son] < arr[son + 1])
//先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大於子节点代表调整完毕,直接跳出函数
return;
else //否则交换父子内容再继续子节点和孙节点比较
{
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort1(int arr[], int len)
{
int i;
//初始化,i从最後一个父节点开始调整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
//先将第一个元素和已排好元素前一位做交换,再重新调整,直到排序完毕
for (i = len - 1; i > 0; i--)
{
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
8.归并排序
| 时间复杂度 | |
|---|---|
| 空间复杂度 | O(n) |
| 稳定性 | 稳定 |
时间复杂度:
O ( n l o g 2 n ) {O(nlog_2{n})} O(nlog2n)
思路:
数组数组不断进行分组,直到组内数组只有一个为止,就可以进行合并操作mergArr(arr,left,right) [left,mid] [mid+1,right]有序 合并成 arr[left,right]整体有序
图解:https://www.jianshu.com/p/33cffa1ce613
8 6 1 5 4 3 9 0 2 7
0 9
4
8 6 1 5 4 3 9 0 2 7
8 6 1 5 4
6 8 1 4 5
1 4 5 6 8 0 2 3 7 9
0 1 2 3 4 5 6 7 8 9
调用数组合并的方法
图解:+不一样的思路:https://blog.csdn.net/qq_40907279/article/details/81607634
代码
void mergeArr(int arr[],size_t n){
if(n<=1){
return ;
}
int mid = n/2;
int len =mid;
int *prr = malloc(sizeof(int)*len);
size_t i;
for(i=0;i9.快速排序
| 时间复杂度 | |
|---|---|
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
时间复杂度:
O ( n l o g 2 n ) {O(nlog_2{n})} O(nlog2n)
效果:
思路:
快速排序采用双向查找的策略,每一趟选择当前所有子序列中的一个关键字作为枢纽轴,将子序列中比枢纽轴小的前移,比枢纽轴大的后移,当本趟所有子序列都被枢轴按上述规则划分完毕后将会得到新的一组更短的子序列,他们将成为下趟划分的初始序列集。
时间复杂度:最好情况(待排序列接近无序)时间复杂度为O(nlog2n),最坏情况(待排序列接近有序)时间复杂度为O(n2),平均时间复杂度为O(nlog2n)。
-
找一个基准值 把该基准值放到合适的位置;
-
用一个临时变量去存储基准数据;
-
先从后往前扫,如果扫描到的值大于基准数据就让right减1,如果发现有元素比该基准数据的值小,就将right位置的值赋值给left位置;
-
然后从前往后扫描,如果扫描到的值小于基准数据就让left加1,如果发现有元素大于基准数据的值,就再将left位置的值赋值给right位置的值;
-
再开始从后向前扫描,原理同上;
-
直到left=right,或者right>left;
本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边,这样就找到了该数据在数组中的正确位置
最后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时,整个数组就有序了。
[left,right]
int key = arr[left];
i=left,j=right;
只要i 首先从右边找小于key的值放到arr[i]位置 然后从左边找大于key的值放到arr[j]位置 当i arr[i] = key 它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。理论下线位O(n*log(n)). 扫描整个集合S,对每一个Si∈S,找到在线性表L中小于等于Si的元素的个数T(Si); 扫描整个线性表L,对L中的每一个元素Li,将Li放在输出线性表的第T(Li)个位置上,并将T(Li)减1。 其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 适用:数据比较集中 是计数排序的升级版本 大致对所有数据进行分类 把"类型"相同的放到一块排序,把大量数据分割成了基本有序的数据块(桶),然后只需要对桶中的少量数据做先进的比较排序 桶排序复杂度以及稳定性: 桶排序利用函数的映射关系,减少了几乎所有的比较工作。实际上,桶排序的f(k)值的计算,其作用就相当于快排中划分,已经把大量数据分割成了基本有序的数据块(桶),然后只需要对桶中的少量数据做先进的比较排序。 对N个关键字进行桶排序的时间复杂度分为两个部分: (1) 循环计算每个关键字的桶映射函数,这个时间复杂度是O(N)。 (2) 利用先进的比较排序算法对每个桶内的所有数据进行排序,其时间复杂度为 ∑ O(Ni*logNi) 。其中Ni 为第i个桶的数据量。 很显然,第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到O(N*logN)了)。因此,我们需要尽量做到下面两点: (1) 映射函数f(k)能够将N个数据平均的分配到M个桶中,这样每个桶就有[N/M]个数据量。 (2) 对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为: O(N)+O(M*(N/M)log(N/M))=O(N+N(logN-logM))=O(N+NlogN-NlogM) 当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。 总结: 桶排序的平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。最好的时间复杂度为O(N)。 当然桶排序的空间复杂度 为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价无疑是昂贵的。 桶排序是稳定的。 详解引用:https://blog.csdn.net/s04103037/article/details/9997915 排序快慢是数量 动态划分 把最大数找到,用来判断最高位。同时用于终止循环, 根据位上的数字,来判断大小放到相应的桶里,数放完后,再将每个数提取出放回原来的数组里,同时也知道了每个数的新下标。按照位来依次循环,直到循环结束,按照顺序依次输出。 其他图解,思路,来源于网络:https://cloud.tencent.com/developer/news/326060 7 68 98 388 19 29 199 其他图解,思路,来源于网络:https://cloud.tencent.com/developer/news/326060 图片来自于网络,侵删。代码
void quick(int arr[],int left,int right){
if(left >= right)
return;
int i=left,j=right;
int key = arr[i];
while(ivoid quick_sort(int arr[],size_t n){
if(n<=1){
return;
}
size_t i=0,j=n-1;
int key =arr[i];
while(i10.计数排序
时间复杂度
空间复杂度
O(n)
稳定性
稳定
思想:
代码
void count_sort(int arr[],size_t n){
int max = arr[0];
int min = arr[0];
size_t i;
for(i=0;i11.桶排序
时间复杂度
O(N)
空间复杂度
O(N+M)
稳定性
稳定
思路:
代码
typedef struct Bucket{
int cnt;
int vect[100];
}Bucket;
void bucket_sort(int arr[],size_t n){
int max = arr[0];
int min = arr[0];
size_t i;
for(i=0;ivoid bucketSort(int *arr, int size, int max)
{
int i,j;
int buckets[max];
memset(buckets, 0, max * sizeof(int));
for (i = 0; i < size; i++) {
buckets[arr[i]]++;
}
for (i = 0, j = 0; i < max; i++) {
while((buckets[i]--) >0)
arr[j++] = i;
}
12.基数排序
时间复杂度
O(N*M)
空间复杂度
O(M)
稳定性
不稳定
思路
过程:
低位优先排序 LSD: Least Significant Digist first
高位优先排序 MSD: Most Significant Digist first 递归
19 29 34 100 27 30 37 68 11 7 6 34 98 23 44 32 199
277 343 276 388 291 7 4 5 23
最大只有三位数
个位:
0: 100
1: 11 291
2: 32
3: 23 343 23
4: 34 34 44 4
5: 5
6: 6 276
7: 27 7 277 7
8: 68 98 388
9: 19 29 199
100 11 291 32 23 343 23 34 34 44 4 5 6 276 27 7 277 7 68 98 388 19 29 199
十位:
0: 100 4 5 6 7 7
1: 11 19
2: 23 23 27 29
3: 32 34 34
4: 343 44
5:
6: 68
7: 276 277
8: 388
9: 291 98 199
100 4 5 6 7 7 11 19 23 23 27 29 32 34 34 343 44 68 276 277 388 291 98 199
百位:
0: 4 5 6 7 7 11 19 23 23 27 28 32 34 34 44 68 98
1: 100 199
2: 276 277 291
3: 343 388
4:
5:
6:
7:
8:
9:
4 5 6 7 7 11 19 23 23 27 28 32 34 34 44 68 98 100 199 276 277 291 343 388
代码
void base_sort(int arr[],size_t n){
Bucket bucket[10] = {};
int max = arr[0];
size_t i;
for(i=0;i十位:
0: 100 4 5 6 7 7
1: 11 19
2: 23 23 27 29
3: 32 34 34
4: 343 44
5:
6: 68
7: 276 277
8: 388
9: 291 98 199
100 4 5 6 7 7 11 19 23 23 27 29 32 34 34 343 44 68 276 277 388 291 98 199
百位:
0: 4 5 6 7 7 11 19 23 23 27 28 32 34 34 44 68 98
1: 100 199
2: 276 277 291
3: 343 388
4:
5:
6:
7:
8:
9:
4 5 6 7 7 11 19 23 23 27 28 32 34 34 44 68 98 100 199 276 277 291 343 388
代码
void base_sort(int arr[],size_t n){
Bucket bucket[10] = {};
int max = arr[0];
size_t i;
for(i=0;i