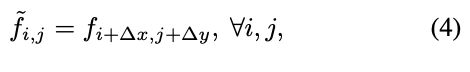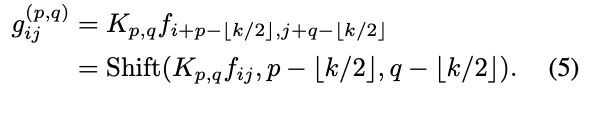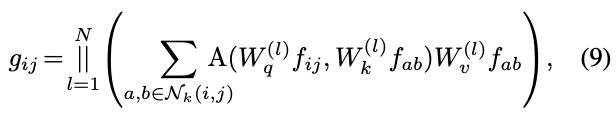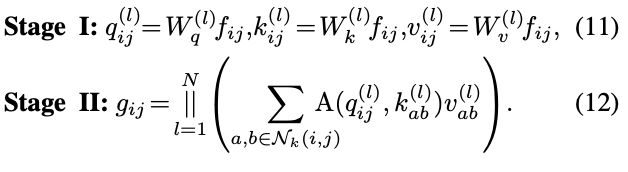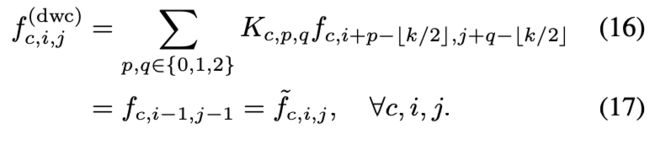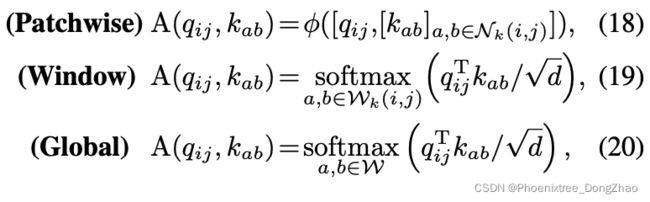自注意力和 CNN 的结合 ACmix : On the Integration of Self-Attention and Convolution

On the Integration of Self-Attention and Convolution

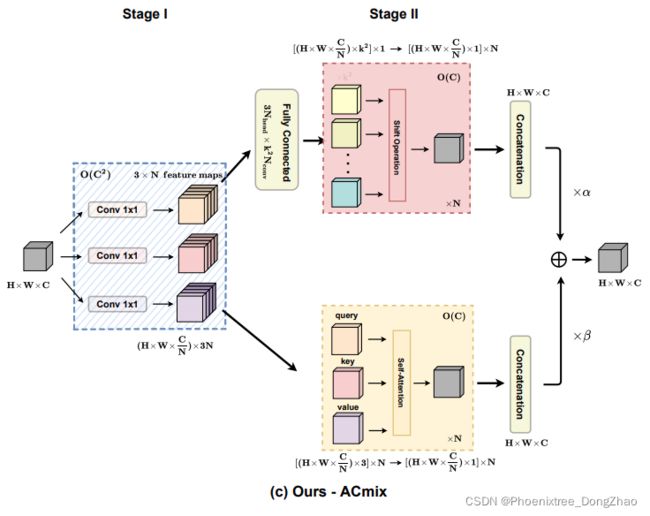
Figure 1. A sketch of ACmix. We explore a closer relationship between convolution and self-attention in the sense of sharing the same computation overhead (1×1 convolutions), and combining with the remaining lightweight aggregation operations. We show the computation complexity of each block w.r.t the feature channel.

[pdf]

Code and pre-trained models will be released at https://github.com/Panxuran/ACmix and models: Models of MindSpore.

目录

Abstract

1. Introduction

3. Revisiting Convolution and Self-Attention

3.1. Convolution

3.2. Self-Attention

3.3. Computational Cost

4. Method

4.1. Relating Self-Attention with Convolution

4.2. Integration of Self-Attention and Convolution

4.3. Improved Shift and Summation

4.4. Computational Cost of ACmix

4.5. Generalization to Other Attention Modes

---

Abstract

Convolution and self-attention are two powerful techniques for representation learning, and they are usually considered as two peer approaches that are distinct from each other.

In this paper, we show that there exists a strong underlying relation between them, in the sense that the bulk of computations of these two paradigms are in fact done with the same operation.

Specifically, we first show that a traditional convolution with kernel size k×k can be decomposed into k^2 individual 1×1 convolutions, followed by shift and summation operations. Then, we interpret the projections of queries, keys, and values in self-attention module as multiple 1×1 convolutions, followed by the computation of attention weights and aggregation of the values. Therefore, the first stage of both two modules comprises the similar operation. More importantly, the first stage contributes a dominant computation complexity (square of the channel size) comparing to the second stage. This observation naturally leads to an elegant integration of these two seemingly distinct paradigms, i.e., a mixed model that enjoys the benefit of both self-Attention and Convolution (ACmix), while having minimum computational overhead compared to the pure convolution or self-attention counterpart.

Extensive experiments show that our model achieves consistently improved results over competitive baselines on image recognition and downstream tasks.

卷积和自注意是表示学习的两种强大技术，它们通常被认为是两种彼此不同的对等方法。

本文证明了它们之间存在着一种强烈的潜在关系，即这两种范式的大部分计算实际上是用相同的操作完成的。

具体来说，本文首先证明了一个传统的核大小为 k x k 的卷积可以分解为 k^2 个单独的卷积，然后进行移位和求和操作。然后，将自注意模块中的 query、key 和 value 的投影解释为多个 1x1 卷积，然后计算注意力权重和值的聚合。因此，这两个模块的第一阶段包含类似的操作。更重要的是，与第二阶段相比，第一阶段的计算复杂度 (通道大小的平方) 占主导地位。这种观察自然地导致了这两个看起来截然不同的范式的优雅集成，也就是说，混合模型 ACmix 可以同时享受自注意和卷积的好处，同时与纯卷积或自注意对应的模型相比，具有最小的计算开销。

大量的实验表明，本文的模型在图像识别和下游任务上取得了比 具有竞争力都 baseline 一致的改进结果。

1. Introduction

Recent years have witnessed the vast development of convolution and self-attention in computer vision. Convolution neural networks (CNNs) are widely adopted on image recognition [20, 24], semantic segmentation [9] and object detection [39], and achieve state-of-the-art performances on various benchmarks. On the other hand, self-attention is first introduced in natural language processing [1, 43], and also shows great potential in the fields of image generation and super-resolution [10, 35]. More recently, with the advent of vision transformers [7,16,38], attention-based modules have achieved comparable or even better performances than their CNN counterparts on many vision tasks.

简述本文两大核心技术的发展情况：

近年来，卷积和自注意技术在计算机视觉中的应用得到了极大的发展。卷积神经网络被广泛应用于图像识别、语义分割和目标检测，并在各种基准上取得了最先进的性能。另一方面，自注意力首先在自然语言处理中被引入，在图像生成和超分辨率领域也显示出巨大的潜力。最近，随着 vision transformer 的出现，基于注意力的模块在许多视觉任务上取得了与 CNN 相当甚至更好的性能。

Despite the great success that both approaches have achieved, convolution and self-attention modules usually follow different design paradigms. Traditional convolution leverages an aggregation function over a localized receptive field according to the convolution filter weights, which are shared in the whole feature map. The intrinsic characteristics impose crucial inductive biases for image processing. Comparably, the self-attention module applies a weighted average operation based on the context of input features, where the attention weights are computed dynamically via a similarity function between related pixel pairs. The flexibility enables the attention module to focus on different regions adaptively and capture more informative features.

简析本文两大核心技术的本质特点：

尽管这两种方法都取得了巨大的成功，卷积和自注意模块通常遵循不同的设计范式。传统的卷积是根据卷积滤波器的权值在局部接受域上利用一个聚合函数，这些权值在整个特征图中共享。内在特性对图像处理有重要的归纳偏差（inductive biases）。相比之下，自注意模块采用基于输入特征上下文的加权平均操作，其中通过相关像素对之间的相似函数动态计算注意权重。这种灵活性使注意力模块能够自适应地聚焦于不同的区域，并捕捉更多的信息特征。

Considering the different and complementary properties of convolution and self-attention, there exists a potential possibility to benefit from both paradigms by integrating these modules. Previous work has explored the combination of self-attention and convolution from several different perspectives.

Researches from early stages, e.g., SENet [23], CBAM [47], show that self-attention mechanism can serve as an augmentation for convolution modules.

More recently, self-attention modules are proposed as individual blocks to substitute traditional convolutions in CNN models, e.g., SAN [54], BoTNet [41].

Another line of research focuses on combining self-attention and convolution in a single block, e.g., AA-ResNet [3], Container [17], while the architecture is limited in designing independent paths for each module.

Therefore, existing approaches still treat self-attention and convolution as distinct parts, and the underlying relations between them have not been fully exploited.

考虑到卷积和自我注意的不同和互补性质，通过集成这些模块，存在从这两种范式中获益的潜在可能性。之前的研究已经从几个不同的角度探讨了自我注意和卷积的结合。

第一种，将自注意机制作为卷积模块的增强，如 SENet、CBAM；

第二种，将自注意模块作为单个块来替代 CNN 模型中的传统卷积，如 SAN、BoTNet。

第三种，将自注意和卷积结合在一个块中，例如 AA-ResNet， Container，但体系结构在为每个模块设计独立路径方面存在局限性。

SAN ：    Exploring self-attention for image recognition. CVPR, 2020.

BoTNet：Bottleneck transformers for visual recognition. CVPR, 2021.

AA-ResNet：Attention augmented convolutional networks. CVPR, 2019.

Container：  Container: Context aggregation network. 2021.

总之，现有的方法仍然将自注意力和卷积视为两个不同的部分，它们之间的内在联系还没有被充分挖掘。

In this paper, we seek to unearth a closer relationship between self-attention and convolution. By decomposing the operations of these two modules, we show that they heavily rely on the same 1×1 convolution operations. Based on this observation, we develop a mixed model, named ACmix, and integrate self-attention and convolution elegantly with minimum computational overhead. Specifically, we first project the input feature maps with 1×1 convolutions and obtain a rich set of intermediate features. Then, the intermediate features are reused and aggregated following different paradigms, i.e, in self-attention and convolution manners respectively. In this way, ACmix enjoys the benefit of both modules, and effectively avoids conducting expensive projection operations twice.

本文试图揭示自注意力和卷积之间的一个更密切的关系。

通过分解这两个模块的运算，作者发现它们在很大程度上依赖于相同的 1x1 卷积运算。

基于这一观察，本文开发了一个名为 ACmix 的混合模型，并以最小的计算开销优雅地集成了自注意力和卷积。

具体来说，首先，用 1x1 卷积投影输入特征映射，得到一个丰富的中间特征集。然后，按照自注意力和卷积两种不同的模式对中间特征进行重用和聚合。

通过这种方式，ACmix 享有了两个模块的好处，并有效地避免了两次执行高复杂度的投影操作。

To summarize, our contributions are two folds:

(1) A strong underlying relation between self-attention and convolution is revealed, providing new perspectives on understanding the connections between two modules and inspirations for designing new learning paradigms.

(2) An elegant integration of the self-attention and convolution module, which enjoys the benefits of both worlds, is presented. Empirical evidence demonstrates that the hybrid model outperforms its pure convolution or selfattention counterpart consistently.

综上所述，本文的贡献有两个方面:

(1) 揭示了自注意力和卷积之间强烈的潜在关系，为理解两个模块之间的联系提供了新的视角，并为设计新的学习范式提供了灵感。

(2) 优雅地集成了自注意力和卷积模块，同时享有两个世界的好处。经验证据表明，混合模型的性能优于纯卷积模型或自注意力的模型。

3. Revisiting Convolution and Self-Attention

3.1. Convolution

Convolution is one of the most essential parts of modern ConvNets. We first review the standard convolution operation and reformulate it from a different perspective. The illustration is shown in Fig.2(a). For simplicity, we assume the stride of convolution is 1.

Consider a standard convolution with the kernel K ∈ , where k is the kernel size and C_in, C_out are the input and output channel size. Given tensors  F∈ , G∈  as the input and output feature maps, where H, W denote the height and width, we denote as the feature tensors of pixel (i, j) corresponding to F and G respectively. Then, the standard convolution can be formulated as:

where ，represents the kernel weights with regard to the indices of the kernel position (p, q).

卷积图示如图 2(a) 所示。为了简单起见，假设卷积的 stride 是 1。

Figure 2. (a) Convolution. The output of a 3×3 convolution can be decomposed as a summation of shifted feature maps, where each feature map is obtained by performing a 1×1 convolution concerning the kernel weights from a certain position. s(x, y) corresponds to the Shift operation defined in Sec.3.1. 

给定一个与核 K∈  的标准卷积，其中 K 是核大小，C_in、C_out 是输入和输出通道大小。给定张量 F∈ , G∈作为输入和输出的特征映射，其中 H, W 表示高度和宽度，用  分别为 F 和 G 对应的像素 (i, j) 的特征张量。那么，标准卷积可以表示为 (1)。其中  ，，表示核在位置 (p, q) 的权重

For convenience, we can rewrite Eq.(1) as the summation of the feature maps from different kernel positions:

To further simplify the formulation, we define the Shift operation, , as: 

 

 where ∆x, ∆y correspond to the horizontal and vertical displacements. Then, Eq.(3) can be rewritten as:

As a result, the standard convolution can be summarized as two stages:

At the first stage, the input feature map is linearly projected w.r.t. the kernel weights from a certain position, i.e., (p, q). This is the same as a standard 1 × 1 convolution. While in the second stage, the projected feature maps are shifted according to the kernel positions and finally aggregated together. It can be easily observed that most of the computational costs are performed in the 1×1 convolution, while the following shift and aggregation are lightweight.

为了方便起见，可以将式 (1) 重写为不同内核位置的特征映射的和，即公式（2）和（3）。

为了进一步简化公式，将移位运算定义为（4）。

其中，∆x，∆y分别对应水平位移和垂直位移。那么，Eq.(3) 可以改写为（5）。

因此，标准卷积可以归纳为两个阶段，即公式（6）、（7）和（8）。

在第一阶段，将输入的 feature map 按照核权重，从某一位置 (p, q) 进行线性投影，这相当于标准的 1 × 1 卷积。而在第二阶段，投影的特征映射根据核位置进行移动，最后进行聚合。可以很容易地看到，大多数计算代价是在 1×1 卷积中执行的，而后面的移位和聚合是轻量级的。

3.2. Self-Attention

Attention mechanism has also been widely adopted in vision tasks. Comparing to the traditional convolution, attention allows the model to focus on important regions within a larger size context. We show the illustration in Fig.2(b).

Consider a standard self-attention module with N heads. Let ， denote the input and output feature. Let denote the corresponding tensor of pixel (i, j). Then, output of the attention module is computed as: 

where || is the concatenation of the outputs of N attention heads, and are the projection matrices for queries, keys and values. represents a local region of pixels with spatial extent k centered around (i, j), and is the corresponding attention weight with regard to the features within .

注意力机制也被广泛应用于视觉任务中。与传统的卷积相比，注意力可以让模型在更大的范围内聚焦于重要区域。如图 2(b) 所示。

Figure 2. (b) Self-Attention. Input feature map is first projected as queries, keys, and values with 1×1 convolutions. The attention weights computed by queries and keys are adopted to aggregate the values. The right figure shows the pipeline of our module.

考虑一个有 N 个 head 的标准自注意力模块。设 ，表示输入和输出特征。设表示像素 (i, j) 对应的张量，则计算注意模块的输出为（9）。

其中 || 是 N 个注意头输出的级联，是query、key 和 value 的投影矩阵。表示以 (i, j) 为中心，空间宽度为 k 的像素的局部区域，为关于对应的权重。

For the widely adopted self-attention modules in [21,38], the attention weights are computed as:

 

where d is the feature dimension of . 

Also, multi-head self-attention can be decomposed into two stages, and reformulated as:

Similar to the traditional convolution in Sec.3.1, 1×1 convolutions are first conducted in stage I to project the input feature as query, key and value. On the other hand, Stage II comprises the calculation of the attention weights and aggregation of the value matrices, which refers to gathering local features. The corresponding computational cost is also proved to be minor comparing to Stage I, following the same pattern as convolution.

广泛采用的自注意模块计算注意力权值为（10）所示。

其中 d 为的特征维数。

同时，多头自注意力可以分解为两个阶段，重新表述为（11）和（12）。

与第 3.1 节中传统的卷积相似，在第一阶段首先进行 1×1 卷积，将输入特征投影为 query、key 和 value。第二阶段包括注意权值的计算和值矩阵的聚合，即收集局部特征。与阶段 I 相比，相应的计算代价也被证明较小，遵循与卷积相同的模式。

​

3.3. Computational Cost

To fully understand the computation bottleneck of the convolution and self-attention modules, we analyse the floating-point operations (FLOPs) and the number of parameters at each stage and summarize in Tab.1. It is shown that theoretical FLOPs and parameters at Stage I of convolution have quadratic complexity with regard to the channel size C, while the computational cost for Stage II is linear to C and no additional training parameters are required.

A similar trend is also found for the self-attention module, where all training parameters are preserved at Stage I. As for the theoretical FLOPs, we consider a normal case in a ResNet-like model where ka = 7 and C = 64, 128, 256, 512 for various layer depths. It is explicitly shown that Stage I consumes a heavier operation as , and the discrepancy is more distinct as channel size grows.

To further verify the validity of our analysis, we also summarize the actual computational costs of the convolution and self-attention modules in a ResNet50 model in Tab.1. We practically add up the costs of all 3×3 convolution (or self-attention) modules to reflect the tendency from the model perspective. It is shown that 99% computation of convolution and 83% of self-attention are conducted at Stage I, which are consistent with our theoretical analysis.

为了充分了解卷积模块和自注意力模块的计算瓶颈，本文分析了各个阶段的浮点运算 (FLOPs) 和参数个数，总结如表 1 所示。结果表明，卷积的理论 FLOPs 和阶段I的参数与通道大小 C 具有二次方复杂度，而阶段 II 的计算代价与 C 呈线性关系，不需要额外的训练参数。

对于理论FLOPs，作者认为在 ResNet-like 模型中是一种正常情况，对于不同层深，k_a = 7, C = 64、128、256、512。可以清楚地看出，阶段 I 消耗了更大的操作，即，并且随着通道尺寸的增大，差异更加明显。

为了进一步验证上述分析的有效性，本文还在表 1 中总结了 ResNet50 模型中卷积模块和自注意力模块的实际计算代价。实际上将所有 3×3 卷积 (或自注意力) 模块的成本相加，以反映从模型角度来看的趋势。结果表明，在第一阶段进行了 99% 的卷积计算和 83% 的自注意力计算，这与前面的理论分析是一致的。
 

4. Method

4.1. Relating Self-Attention with Convolution

The decomposition of self-attention and convolution modules in Sec.3 has revealed deeper relations from various perspectives.

First, the two stages play quite similar roles. Stage I is a feature learning module, where both approaches share the same operations by performing 1×1 convolutions to project features into deeper spaces. On the other hand, stage II corresponds to the procedure of feature aggregation, despite the differences in their learning paradigms.

From the computation perspective, the 1 × 1 convolutions conducted at Stage I of both convolution and selfattention modules require a quadratic complexity of theoretical FLOPs and parameters with regard to the channel size C. Comparably, at stage II both modules are lightweight or nearly free of computation.

As a conclusion, the above analysis shows that (1) Convolution and self-attention practically share the same operation on projecting the input feature maps through 1×1 convolutions, which is also the computation overhead for both modules. (2) Although crucial for capturing semantic features, the aggregation operations at stage II are lightweight and do not acquire additional learning parameters.

第 3 章对自注意力和卷积模块的分解从多个角度，揭示了更深层次的关系。

首先，这两个阶段扮演的角色非常相似。

第一阶段是一个特征学习模块，这两种方法共享相同的操作，通过执行 1×1 卷积将特征投射到更深层的空间。

第二阶段对应特征聚合的过程，两种学习模式存在差异。

其次，从计算的角度来看，

在第一阶段，卷积模块和自注意模块进行的 1 × 1 卷积，都需要在理论上的 FLOPs 和参数量上呈现通道数 C 二次方的复杂度。

在第二阶段，两个模块都是轻量级的或几乎不需要计算。

综上所述，(1) 卷积和自注意力在通过 1×1 卷积投影输入特征映射上实际上有相同的操作，这也是两个模块的计算开销。

(2) 虽然聚合操作对语义特征的获取至关重要，但第二阶段的聚合操作是轻量级的，不需要获取额外的学习参数。

4.2. Integration of Self-Attention and Convolution

The aforementioned observations naturally lead to an elegant integration of convolution and self-attention. As both modules share the same 1×1 convolution operations, we can only perform the projection once, and reuse these intermediate feature maps for different aggregation operations respectively. The illustration of our proposed mixed module, ACmix, is shown in Fig.2(c).

Specifically, ACmix also comprises two stages. At Stage I, the input feature is projected by three 1×1 convolutions and reshaped into N pieces, respectively. Thus, we obtain a rich set of intermediate features containing 3×N feature maps.

At Stage II, they are used following different paradigms. For the self-attention path, we gather the intermediate features into N groups, where each group contains three pieces of features, one from each 1×1 convolution. The corresponding three feature maps serve as queries, keys, and values, following the traditional multi-head self-attention modules (Eq.(12)). For the convolution path with kernel size k, we adopt a light fully connected layer and generate k^2 feature maps. Consequently, by shifting and aggregating the generated features (Eq.(7),(8)), we process the input feature in a convolution manner, and gather information from a local receptive field like the traditional ones.

Finally, outputs from both paths are added together and the strengths are controlled by two learnable scalars:

上述的观察结果自然地导致了卷积和自注意力的优雅集成。由于这两个模块共享相同的 1×1 convolution 操作，本文只能执行一次投影，并重用这些中间特征映射分别用于不同的聚合操作。本文提出的混合模块 ACmix 如图 2(c) 所示。

Figure 2. (c) ACmix. At stage I, the input feature map is projected with three 1×1 convolutions. At stage II, the intermediate features are used following two paradigms respectively. Features from both paths are added together and serve as the final output. The computational complexity of each operation block is marked at the upper corner. 

具体来说，ACmix 还包括两个阶段。在阶段 I，输入特征通过三个 1×1 卷积进行投影，分别重塑成N 个片段。这样，得到了一个包含 3×N feature map 的丰富的中间特征集。

在第 II 阶段，它们是按照不同的范式使用的。对于自注意力路径，本文将中间特征集合成 N 组，每组包含 3 个特征，其中一个来自 1×1 卷积。对应的三个特征映射作为 query、key 和 value，遵循传统的多头自注意力模块 (式 (12))。对于核大小为 k 的卷积路径，采用一个轻全连通层，生成 k^2 个特征图。因此，通过移动和聚合生成的特征 (Eq.(7)，(8))，以卷积的方式处理输入特征，并像传统的接收域一样从局部接收域收集信息。

最后，两条路径的输出相加，强度由两个可学习的标量控制，如公式（13）。

4.3. Improved Shift and Summation

As shown in Sec.4.2 and Fig.2, intermediate features in the convolution path follow the shift and summation operations as conducted in traditional convolution modules. Despite that they are theoretically lightweight, shifting tensors towards various directions practically breaks the data locality and is difficult to achieve vectorized implementation. This may greatly impair the actual efficiency of our module at the inference time.

As a remedy, we resort to applying depthwise convolution with fixed kernels as a replacement of the inefficient tensor shifts, as shown in Fig.3 (b). Take Shift(f, −1, −1) as an example, shifted feature is computed as:

 where c represents each channel of the input feature.

如 4.2 节和图 2 所示，卷积路径中的中间特征遵循传统卷积模块的移位和求和操作。尽管它们在理论上是轻量级的，但将张量向各个方向移动实际上打破了数据局部性，并且难以实现向量化实现。这可能会极大地损害本文模块在推理时的实际效率。

作为补救方法，本文采用固定核的深度卷积来替代无效张量位移，如图 3 (b) 所示。以 Shift (f，−1，−1) 为例，移位特征计算如（14）。

其中 C 表示输入特征的每个通道。

​

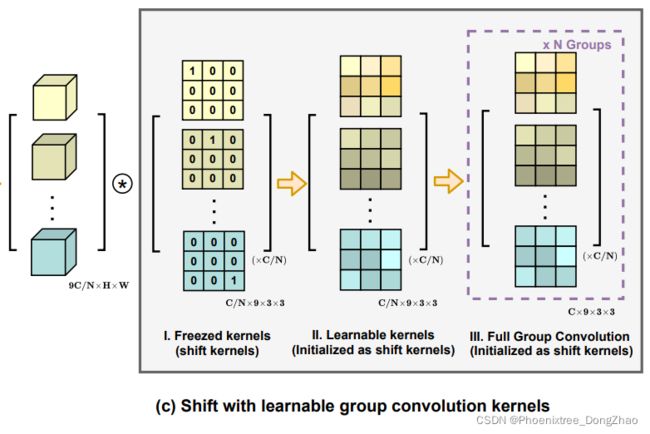
Figure 3. (b) Fast implementation with carefully designed group convolution kernels.

On the other hand, if we denote convolution kernel (kernel size k = 3) as:

 the corresponding output can be formulated as:

Therefore, with carefully designed kernel weights for specific shift directions, the convolution outputs are equivalent to the simple tensor shifts (Eq.(14)). To further incorporate with the summation of features from different directions, we concatenate all the input features and convolution kernels respectively, and formulate shift operation as a single group convolution, as depicted in Fig.3 (c.I). This modification enables our module with higher computation efficiency.

On this basis, we additionally introduce several adaptations to enhance the flexibility of the module. As shown in Fig.3 (c.II), we release the convolution kernel as learnable weights, with shift kernels as initialization. This improves the model capacity while maintaining the ability of original shift operations. We also use multiple groups of convolution kernels to match the output channel dimension of convolution and self-attention paths, as depicted in Fig.3 (c.III).

另一方面，如果将卷积核 (核大小 k = 3) 表示为（15），相应的输出可以表示为（16）和（17）。

因此，对于特定的位移方向，经过精心设计的核权值，卷积输出等价于简单张量位移 (式 (14))。为了进一步结合不同方向特征的总和，本文将所有输入特征和卷积核分别串联起来，将移位操作表示为单个组卷积，如图 3 (c.I) 所示。这一修改使本文的模块具有更高的计算效率。

在此基础上，本文还介绍了几个增强模块灵活性的适配。如图 3 (c.II) 所示，本文展示卷积核为可学习权值，平移核为初始化。这提高了模型容量，同时保持原有的移位操作能力。本文还使用多组卷积核来匹配卷积和自注意力路径的输出通道维数，如图 3 (c.III) 所示。

Figure 3. (c) Further adaptations with learnable kernels and multiple convolution groups.

4.4. Computational Cost of ACmix

For better comparison, we summarize the FLOPs and parameters of ACmix in Tab.1. The computational cost and training parameters at Stage I are the same as self-attention and lighter than traditional convolution (e.g., 3×3 conv). At Stage II, ACmix introduces additional computation overhead with a light fully connected layer and a group convolution described in Sec.4.3, whose computation complexity is linear with regard to channel size C and comparably minor with Stage I. The practical cost in a ResNet50 model shows similar trends with theoretical analysis.

为了更好的比较，在表 1 中总结了 ACmix 的 FLOPs 和参数。第 I 阶段的计算代价和训练参数与自注意力相同，比传统的卷积 (如 3×3 conv) 更轻。在第 II 阶段，ACmix 引入了额外的计算开销，包括一个轻量级全连接层和一组卷积，其计算复杂度为通道大小 C 线性关系，与第 I 阶段比小了很多。ResNet50 模型的实际成本显示出与理论分析相似的趋势。

4.5. Generalization to Other Attention Modes

With the development of the self-attention mechanism, numerous researches have focused on exploring variations of the attention operator to further promote the model performance. Patchwise attention proposed by [54] incorporates information from all features in the local region as the attention weights to replace the original softmax operation. Window attention adopted by Swin-Transformer [32] keeps the same receptive field for tokens in the same local window to save computational cost and achieve fast inference speed. ViT and DeiT [16,42], on the other hand, consider global attention to retaining long-range dependencies within a single layer. These modifications are proved to be effective under specific model architectures.

Under the circumstance, it is worth noticing that our proposed ACmix is independent of self-attention formulations, and can be readily adopted on the aforementioned variants. Specifically, the attention weights can be summarized as:

where [·] refers to feature concatenation, φ(·) represents two linear projection layers with an intermediate nonlinear activation, Wk(i, j) is the specialized receptive field for each query token, and W represents the whole feature map (Please refer to the original paper for further details). Then, the computed attention weights can be applied to Eq.(12) and fits into the general formulation.

随着自注意力机制的发展，许多研究都集中在探索注意力算子的变化，以进一步提高模型性能。[54] 提出的 Patchwise 注意力将局部区域中所有特征的信息作为注意权值来替代原有的 softmax 操作。Swin-Transformer 采用的窗口注意对同一个本地窗口中的 tokens 保持相同的感受野，以节省计算成本，实现快速推理速度。另一方面，ViT 和 DeiT 考虑在单个层中保持长期依赖关系的全局注意力。在特定的模型体系结构下，这些修改被证明是有效的。

在这种情况下，值得注意的是，本文提出的 ACmix 是独立于自注意力公式的，可以很容易地在上述变体中采用。具体来说，注意力权重可以总结为（18），（19）和（20）。

其中 [·] 为特征连接，φ(·) 为两个中间非线性激活的线性投影层，W_k(i, j) 为每个 query token 特定的感受野，W 为整个特征映射。然后，计算得到的注意力权重可以应用到式 (12) 中，并拟合到一般公式中。

​