Python数值求解微分方程(欧拉法,隐式欧拉)
不说什么,先上代码
这里先求解形如![]() 的微分方程
的微分方程
1.欧拉法
def eluer(rangee,h,fun,x0,y0):
step = int(rangee/h)
x = [x0] + [h * i for i in range(step)]
u = [y0] + [0 for i in range(step)]
for i in range(step):
u[i+1] = u[i] + h * fun(x[i],u[i])
plt.plot(x,u,label = "eluer")
return u
2.隐式欧拉法
def implicit_euler(rangee,h,fun,x0,y0):
step = int(rangee/h)
x = [x0] + [h * i for i in range(step)]
u = [y0] + [0 for i in range(step)]
v = ["null"] + [0 for i in range(step)]
for i in range(step):
v[i+1] = u[i] + h * fun(x[i],u[i])
u[i+1] = u[i] + h/2 * (fun(x[i],u[i]) + fun(x[i],v[i+1]))
plt.plot(x,u,label = "implicit eluer")
return u
3.三阶runge-kutta法
def order_3_runge_kutta(rangee,h,fun,x0,y0):
step = int(rangee/h)
k1,k2,k3 = [[0 for i in range(step)] for i in range(3)]
x = [x0] + [h * i for i in range(step)]
y = [y0] + [0 for i in range(step)]
for i in range(step):
k1[i] = fun(x[i],y[i])
k2[i] = fun(x[i]+0.5*h,y[i]+0.5*h*k1[i])
k3[i] = fun(x[i]+0.5*h,y[i]+2*h*k2[i]-h*k1[i])
y[i+1] = y[i] + 1/6 * h * (k1[i]+4*k2[i]+k3[i])
plt.plot(x,y,label = "order_3_runge_kutta")
return y
4.四阶runge-kutta法
def order_4_runge_kutta(rangee,h,fun,x0,y0):
step = int(rangee/h)
k1,k2,k3,k4 = [[0 for i in range(step)] for i in range(4)]
x = [x0] + [h * i for i in range(step)]
y = [y0] + [0 for i in range(step)]
for i in range(step):
k1[i] = fun(x[i],y[i])
k2[i] = fun(x[i]+0.5*h,y[i]+0.5*h*k1[i])
k3[i] = fun(x[i]+0.5*h,y[i]+0.5*h*k2[i])
k4[i] = fun(x[i]+h,y[i]+h*k3[i])
y[i+1] = y[i] + 1/6 * h * (k1[i]+2*k2[i]+2*k3[i]+k4[i])
plt.plot(x,y,label = "order_4_runge_kutta")
return y
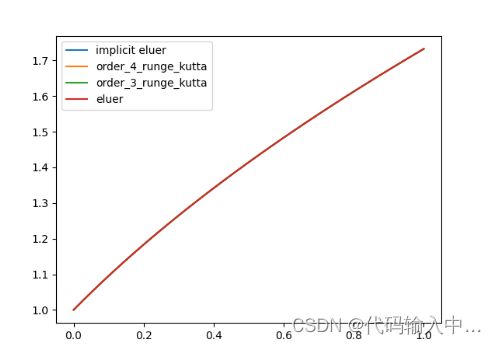
5.上图
当然,想要成功操作,得加上这个
rangee = 1
fun = lambda x,y:y-2*x/y
implicit_euler(rangee,0.0001,fun,0,1)
order_4_runge_kutta(rangee,0.0001,fun,0,1)
order_3_runge_kutta(rangee,0.0001,fun,0,1)
eluer(rangee,0.0001,fun,0,1)
plt.legend()
plt.show()