聚类算法之K-Means 和DBSCAN python实现

这里均采用欧氏距离实现

#实践中，几种相似度计算的比较的重要性往往高于聚类算法本身
class KMEANS(object):
    def __init__(self,n,clusters,data):
        self.results=None#分类结果
        self.n=n
        self.mse=np.zeros(shape=(self.n,))#每轮的簇的均值平方误差
        self.clusters=clusters#簇
        self.data=data#数据

    def eu_dist(self,x,y):#欧氏距离
        return np.sqrt(np.sum(np.square(x-y)))

    def k_means2(self):
        dist=np.array([False])
        c=0
        # while not dist.all():
        while c<40:#更新次数
            # print(dist,self.mse)
            c_dict = {i: [] for i in range(self.n)}#空字典，保存划分的数据
            for i in range(self.data.shape[0]):#遍历所有数据
                min = float('inf')#无穷大
                for j in range(self.n):#判断每个数据到定义的k个中心点的距离
                    d = self.eu_dist(self.data[i], self.clusters[j])

                    if d <= min:
                        count =j#记录最小值对应的中心点
                        min = d#更新最小值
                t = c_dict[count]
                t.append(self.data[i])#将数据保存到所属类别对应的数组中
            self.results = c_dict
            self.clusters=np.zeros(shape=(self.n,self.data.shape[1]))#类型为（n行2列）的零矩阵，这里data.shape[1]为二维坐标点,n为分类数
            mses = []
            for k in range(self.n):
                t = c_dict.get(k)
                mean = np.mean(np.array(t), axis=0)  #求簇均值，更新中心点
                # print(mean)
                std = np.array(t) - mean
                mse1 = np.sum(np.square(std))/(len(t))#最小平方误差
                mses.append(mse1)
                # print(self.clusters,mean.shape)
                self.clusters[k]=mean
            print(self.clusters)

            # print(mses)#均值平方误差
            # dist =np.abs(np.array(mses) - self.mse)
            # # print(dist)
            # dist= np.abs(dist) < 0.001#均值平方误差满足某一阈值则中止算法#这里执行四十次即终止
            # print(dist)
            # self.mse = np.array(mses)
            c+=1
        return self.results

    def color_list(self,color_nums):
        np.random.seed(101)
        curves = [np.random.random(20) for i in range(color_nums)]
        values = range(color_nums)
        jet = cm = plt.get_cmap('jet')
        cNorm = colors.Normalize(vmin=0, vmax=values[-1])
        scalarMap = cmx.ScalarMappable(norm=cNorm, cmap=jet)
        print(scalarMap.get_clim())
        colorVals = [scalarMap.to_rgba(values[i]) for i in range(len(curves))]
        x = np.array(colorVals)
        color_rgb = x[:, :3]
        # print(color_rgb)
        return color_rgb

    def plot(self,data):
        fig = plt.figure()
        ax1 = fig.add_subplot(2, 1, 1)
        ax1.scatter(self.data[:, 0], self.data[:, 1])
        ax2 = fig.add_subplot(2, 1, 2)
        # color = ['r', 'b', 'g', 'gray']
        colors=self.color_list(self.n)
        for i in range(self.n):
            t = np.array(data.get(i))
            ax2.scatter(t[:, 0], t[:, 1], color=colors[i])
        plt.show()
    def start(self):
        self.k_means2()
        # print(self.mse)
        x=self.results
        print(x)
        self.plot(x)

import random
def get_data():

    df=pd.read_csv('datasets/c_0000.csv',na_filter=0)
    #kaggle上下载的star-cluster-simulations数据集中的c_0000.csv
    x1=df.ix[:200,0]
    y1=df.ix[:200,1]
    x2=df.ix[:200,0]+10
    y2=df.ix[:200,1]+10
    x3=df.ix[:200,0]+10
    y3=df.ix[:200,1]-2
    t1=(x1.append(x2)).append(x3)#纵向拼接
    t2=(y1.append(y2)).append(y3)
    data=pd.concat([t1,t2],axis=1)#横向拼接
    # data=list(data)
    data=np.array(data)
    # print(data)
    return data

# n=3
# data=get_data()
# np.random.shuffle(data)
# clusters=data[:n]
# km=KMEANS(n,clusters,data)
# km.start()

'''
对于K-Means的思考：
    K-Means将簇中所有点的均值作为新质心，若簇中含有异常点，将导致均值偏离严重。
    比如，数组 1，2，3，4，100的均值22，显然距离"大多数"数据1，2，3，4比较远，改成求数组的中位数，可能更为稳妥
    ----------K-Mediods聚类（K中值聚类）

如何避免初值的选择对聚类结果造成的影响呢？
    ----二分k-均值聚类：
    计算得到的每个簇的均方误差，若有某些簇的均方误差很大且总是上下波动（不能收敛到较小的值）[可能是该簇划分的不合理]，此时将其切分成2半（类），然后将某两个簇中心较近的两类合成一类
    均方误差多少时才切分为2，一般是先验性的尝试给出
    
    
K-Means聚类方法总结：
    优点： 
        1.解决聚类问题的一种经典算法，简单、快速  
        2.对处理大数据集，该算法保持可伸缩性和高效率 
        3.当结果簇是密集的，它的效果较好
    缺点：
        1.在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用
        2.必须事先给出k（要生成的簇的数目），而且对初值敏感，对于不同的初始值，可能会导致不同结果。
        3.不适合于发现非凸形状的簇或者大小差别很大的簇
        4.对躁声和孤立点数据敏感
    可作为其他聚类方法的基础算法，如谱聚类
'''

#------------------------------------------------------------------------
#层次聚类：对给定的数据集进行层次的分解，直到某种条件满足为止
#AGNES (AGglomerative NESting)算法最初将每个对 象作为一个簇，然后这些簇根据某些准则被一步步 地合并。两个簇间的距离由这两个不同簇中距离最近的数
# 据点对的相似度来确定；聚类的合并过程反复进行直到所有的对象最终满足簇数目
#DIANA (DIvisive ANAlysis)算法是上述过程的反过 程，属于分裂的层次聚类，首先将所有的对象初始 化到一个簇中，然后根据一些原则（比如最大的欧式距离
# ），将该簇分类。直到到达用户指定的簇数目或者两个簇之间的距离超过了某个阈值。

#------------------------------------------------------------------------


密度聚类：

#只要一个区域中的点的密度大于某个阈值，就把它加到与之相近的聚类中去。这类算法能克服基于距 离的算法只能发现“类圆形”(凸)的聚类的缺点，可发现任
# 意形状的聚类，且对噪声数据 不敏感。但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量。

#DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
'''
将簇定义为--密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的数据中发现任意形状的聚类

'''

DBSCAN：

如果一个点p的ε-邻域包含多于m个对象， 则创建一个p作为核心对象的新簇。然后， DBSCAN反复地寻找从这些核心对象直接密 度可达的对象，这个过程可能涉及密度可达 簇的合并。当没有新的点可以被添加到任何 簇时，该过程结束。 

对象的ε-邻域：给定对象在半径ε内的区域。
核心对象：对于给定的数目m，如果一个对象的ε- 邻域至少包含m个对象，则称该对象为核心对象
直接密度可达：给定一个对象集合D，如果p是在q 的ε-邻域内，而q是一个核心对象，我们说对象p 从对象q出发是直接密度可达的
'''
class DBSCAN(object):
    def __init__(self,data,epcilon,m):
        self.data=data
        self.epcilon=epcilon#ε-邻域
        self.limit=m  #邻域内包含对象数
        self.dda=[]#核心对象直接密度可达的点（保存的索引）
        self.cluster={}#保存{核心对象：直接密度可达数组}

    def eu_dist(self,x,y):#欧氏距离
        return np.sqrt(np.sum(np.square(x - y)))
    def is_kenel_object(self,point):#通过给定条件判断是否为核心对象
        dda=[]
        for i in range(self.data.shape[0]):
            dist=self.eu_dist(self.data[i],data[point])
            if dist=self.limit:#判断是否满足点个数
            return True,dda
        return False,dda

    def dbscan(self):
        for i in range(self.data.shape[0]):
            b,dda=self.is_kenel_object(i)
            if b:#如果是核心对象
                if self.cluster:#判断是否已在簇中
                    t=0#记录执行下面for循环次数
                    for k,v in self.cluster.items():

                        if i in v:#判断此核心对象是否是某簇的直接密度可达对象，如果是则合并两个簇

                            vv=list(set(v+dda))
                            self.cluster[k]=vv
                            continue
                        t += 1
                        # else:
                        #     self.cluster[i] = dda
                        #     print(i,'**************')
                    if t==len(self.cluster):#如果次数相等，表明不与其他簇存在交集（密度可达）应当属于新的簇
                        self.cluster[i]=dda
                else:#若为初始状态，添加
                    print('++++++++++++++++++++++')
                    self.cluster[i]=dda

    def color_list(self,color_nums):#利用scalarMap，自动对不同簇调色
        np.random.seed(101)
        curves = [np.random.random(20) for i in range(color_nums)]
        values = range(color_nums)
        jet = cm = plt.get_cmap('jet')
        cNorm = colors.Normalize(vmin=0, vmax=values[-1])
        scalarMap = cmx.ScalarMappable(norm=cNorm, cmap=jet)
        print(scalarMap.get_clim())
        colorVals = [scalarMap.to_rgba(values[i]) for i in range(len(curves))]
        x = np.array(colorVals)
        color_rgb = x[:, :3]
        # print(color_rgb)
        return color_rgb#返回rgb数组，类似[[0.00，0.01，0.50],...,]

    def plot(self):#绘图
        n=150
        # print(self.cluster)
        fig = plt.figure()
        ax1 = fig.add_subplot(2, 1, 1)
        ax1.scatter(self.data[:, 0], self.data[:, 1])
        ax2 = fig.add_subplot(2, 1, 2)
        colors=self.color_list(n)
        for k,v in self.cluster.items():
            for i in v:
                ax2.scatter(self.data[i,0],self.data[i,1] ,color=colors[k])
        plt.show()
    def start(self):
        self.dbscan()
        self.plot()
def circle(num):#生成数据 150行2列
    np.random.seed(1)
    x1=np.linspace(-5,0,num//3)
    y1=np.sqrt(25-x1**2)
    x2=np.linspace(0,9,num//3)
    y2=np.sqrt(81-x2**2)
    x3=np.linspace(-2,2,num//3)
    y3=-np.sqrt(4-x3**2)+2

    dd=np.zeros(shape=(num,2))
    for i in range(len(x1)):
        dd[i,0]=x1[i]
        dd[i,1]=y1[i]
        dd[i+num//3,0]=x2[i]
        dd[i+num//3,1]=y2[i]
        dd[i+(num//3)*2,0]=x3[i]
        dd[i+(num//3)*2,1]=y3[i]
    # print(dd)
    return dd
data=circle(150)

db=DBSCAN(data,2,2)
db.start()

 DBSCAN

密度最大值聚类----只是用作个人记忆和理解（不喜勿喷哦）

参考博客https://blog.csdn.net/u014755255/article/details/80254813

#密度最大值聚类
'''
密度最大值聚类是一种简洁优美的聚类算法, 可以识别各种形状的类簇, 并且参数很容易确定。
'''
class DensityMax():
    def __init__(self,data):
        self.data=data
        self.dist=np.zeros(shape=(len(self.data),len(self.data)))#初始化距离矩阵(对称阵)
    def eu_dist(self):  # 欧氏距离
        distlist=[]
        for i in range(len(self.data)-1):
            for j in range(i+1,len(self.data)):
                distance=np.sqrt(np.sum(np.square(self.data[i]-self.data[j])))
                self.dist[i,j]=distance
                self.dist[j,i]=distance
                if i != j:
                    distlist.append(distance)
        print(distlist)
        return distlist#长度（n(n-1)/2）
    def get_dc(self,distlist):
        '''
        dc是一个截断距离,由于该算法只对局部密度的相对值敏感, 所以对dc的选择是稳健的，一种推荐做法是选择dc，使得平均每个点的邻居数为所有点的1%-2%
        :param distlist:
        :return: dc
        '''

        sortdist = sorted(distlist)
        position = round(len(distlist)* 0.01)
        dc = sortdist[position]
        print('dc', dc)
        return dc
    def calculate_local_density(self,dc):#计算局部密度
        '''
        g(x)= 1(x<0) otherwise g(x)=0 -----
        局部密度ld(i)=∑_j g(dist(i,j)-dc)
        ld(i)即到对象i的距离小于dc的对象的个数
        '''
        ld = np.zeros(len(self.dist))
        # Gaussian kernel
        for i in range(len(self.dist) - 1):
            for j in range(i + 1, len(self.dist)):
                ld[i] += np.exp(-(self.dist[i, j] / dc) **2)#高斯距离
                ld[j] += np.exp(-(self.dist[i, j] / dc) **2)
        ld = [i/max(ld) for i in ld]#标准化
        return ld
    def get_delta(self,ld):#求高局部密度点距离
        '''
        在密度高于对象i的所有对象中，到对象i最近的距离对应的对象
        delta(i)={min(dist(i,j)) | ld(j)>ld(i) all j}
        只有那些密度是局部或者全局最大的点才会有远大于正常值的高局部密度点距离
        '''
        #np.flipud()按列翻转[类似于矩阵行变换]
        #np.argsort()将x中的元素从小到大排列，提取其对应的index(索引)
        order_ld=np.flipud(np.argsort(ld))#局部密度大小降序排列
        delta=np.zeros(len(self.dist))#初始化
        most_close_neighbor=np.zeros(len(self.dist),dtype=int)#比本身密度大，但又最近的点[比我有钱但又差别最小的点]
        delta[order_ld[0]]=-1#order_ld[0]--局部密度最大点的索引
        most_close_neighbor[order_ld[0]]=0
        max_dist=max(self.dist.flatten())#矩阵展平(横向)，返回一维数组，然后求最大距离
        for i in range(1,len(self.dist)):
            delta[order_ld[i]]=max_dist
            for j in range(i):
                #找到高局部密度点距离，即#比本身密度大，但又最近的点,赋值给most_close_neighbor
                #因已进行局部密度降序排列操作，因此这里i之前的均是比本身密度大的点，然后找到二者之间距离最近的
                if self.dist[order_ld[i],order_ld[j]]=limit:#判断是否满足点个数
            return True,dda
        return False,dda

    def classify2(self, center_idx):  # 密度可达的方法进行分类

        '''
        与DBSCAN过程类似

        密度可达：如果存在一个对象链p1p2…pn，p1=q，pn=p，对 pi∈D，(1≤i ≤n)，pi+1是从pi关于ε和m直接密度可达的，则对象p是从对象q关于ε和m密度可达的。
        :param center_idx:
        :return:c
        '''
        pass

    def plot(self,cluster):
        colors=self.color_list(cluster.shape[0])
        fig=plt.figure()
        ax2=fig.add_subplot(1,1,1)
        for i in range(cluster.shape[0]):
            for j in range(cluster.shape[1]) :
                if cluster[i][j]==1:
                    ax2.scatter(self.data[j][0],self.data[j][1],color=colors[i])
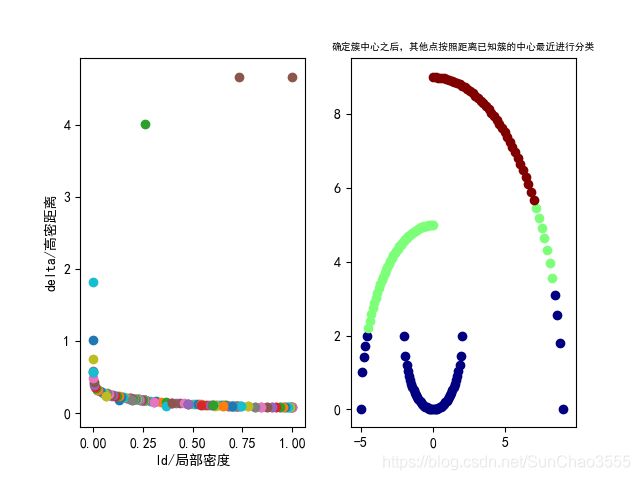
        ax2.set_title('确定簇中心之后，其他点按照距离已知簇的中心最近进行分类',fontsize=7)
        plt.show()

    def start(self):
        distlist=self.eu_dist()
        dc=self.get_dc(distlist)
        ld=self.calculate_local_density(dc)
        most_close_neighbor, delta, order_ld=self.get_delta(ld)
        idx=self.get_cluster_center(ld,delta)
        # cluster=self.classify2(idx)
        cluster=self.classify1(idx)
        self.plot(cluster)
# data=get_data()

dm=DensityMax(data)
dm.start()

 如下图所示，确定簇中心后使用距离最近的已知簇中心分类可能会出现下面情况，因此实践中使用密度可达更为稳妥