OpenCV学习笔记14_常用五种滤波器原理与C++实现(代码在最后)
好久没发blog了,总结一下常用的图像滤波器吧。。。
(感兴趣的同学可以实现一下快速中值滤波:快速中值滤波介绍)
文章目录
- 第1步 、添加噪声(高斯噪声与椒盐噪声)
-
-
- 一、椒盐噪声
- 二、高斯噪声
-
- 1、Box_Muller法生成高斯序列
-
- 空域上的高斯噪声(跟椒盐噪声类似):
- 频域上的高斯噪声:
-
- 第2步 、滤波操作(常用5种滤波器)
-
-
- 一、什么是滤波器
-
- 1、滤波器的定义
- 2、滤波器的分类
- 二、 线性滤波器
-
- 1、方框滤波器
- 2、均值滤波器
- 3、高斯滤波器
- 三、非线性滤波器
-
- 1、中值滤波器
- 2、双边滤波器
- 四、代码
-
第1步 、添加噪声(高斯噪声与椒盐噪声)
一、椒盐噪声
椒盐噪声(salt-and-pepper noise)又称脉冲噪声,它随机改变一些像素值,在二值图像上表现为使一些像素点变白(盐噪声),一些像素点变黑(椒噪声)。 是由图像传感器,传输信道,解码处理等产生的黑白相间的亮暗点噪声。椒盐噪声往往由图像切割引起,去除脉冲干扰及椒盐噪声最常用的算法是中值滤波。
添加椒噪声
//首先添加椒噪声
int n = src.cols*src.rows;//src为读入图像
for (int i = 0 ; i < 0.1*n; i++ )
{
int x = rand() % src.rows;//生成行范围内的随机row值
int y = rand() % src.cols;//生成随机cols值
noise_jy.at<Vec3b>(x, y)[0] = 0;//注意x,y不是坐标(x,y)
noise_jy.at<Vec3b>(x, y)[1] = 0;
noise_jy.at<Vec3b>(x, y)[2] = 0;
}
添加盐噪声
(0.1的盐也有点多了)
for (int i = 0; i < 0.1*n; i++)
{
int x = rand() % src.rows;
int y = rand() % src.cols;
noise_jy.at<Vec3b>(x, y)[0] = 255;
noise_jy.at<Vec3b>(x, y)[1] = 255;
noise_jy.at<Vec3b>(x, y)[2] = 255;
}
二、高斯噪声
1、Box_Muller法生成高斯序列
空域上的高斯噪声(跟椒盐噪声类似):
//利用Box_Muller法生成高斯序列
Point gaus_noise(int x,int y)
{
//x,y为列数与行数
double U1 = rand()/ (double)RAND_MAX;
double U2 = rand()/ (double)RAND_MAX;//产生一个0,1的随机数
double R,theta;
R = sqrt(-2 * log(U1));
theta = 2 * CV_PI*U2;
double gs_x, gs_y;
//表示从中心向四周生成
//标准差为3*(x / 2)
//mu为3*x/2
gs_x = (double)R*cos(theta)*3*(x / 2)+3*x/2 ;//表示3个通道都可能有噪声
gs_y = (double)R*sin(theta)*(y / 2)+y/2;
Point point;
//控制范围
//只生成(0,x)之间
if (gs_x> 3 *x/2 || gs_x <0)
{
return point;
}
//只生成(0,y/2)之间
if (gs_y > y / 2 || gs_y < 0)
{
return point;
}
point.x = gs_x;
point.y = gs_y;
return point;
}
频域上的高斯噪声:
//mu高斯函数的偏移,sigma高斯函数的标准差
double gaus_noise(double sigma, double mu)
{
double U1 = rand() / ((1.0)*RAND_MAX);
double U2 = rand() / ((1.0)*RAND_MAX);
double R, theta,x,y;
R = sqrt(-2 * log(1 - U1));
theta = 2 * CV_PI*U2;
x = R*cos(theta);
y = R*sin(theta);
double rt;
rt = y*sigma + mu;
//因为生成的高斯序列为mu=0 , sigma=1的高斯随机数 , 所以需要添加偏移数与标准差
return rt;
}
第2步 、滤波操作(常用5种滤波器)
一、什么是滤波器
1、滤波器的定义
滤波的在数字信号处理这门课程中的本义是,对各种数字信号中的某一或指定频率进行过滤(也可以理解为不想要的频率),最后筛选出我们想要的频率的信号,这即是滤波的过程,也是目的。
常见的图像噪声如高斯噪声、瑞利噪声、椒盐噪声等这些噪声体现在图像上是对图像造成影响的一些偏差频率,也就是一些像素值不合理像素,阻碍图像信息的获取,因此需要减少不合理像素的存在。
2、滤波器的分类
滤波器本质上是数学运算,根据数学的原则可以将滤波器分为两类:
线性滤波器:
本质上是加权运算,也就是滤波点可以由周围邻近像素点线性表出,如均值,高斯;
非线性滤波器:
可以是多个维度(空间域,像素值域)的权重(双边滤波器),也可以是逻辑运算(中值滤波器);
二、 线性滤波器
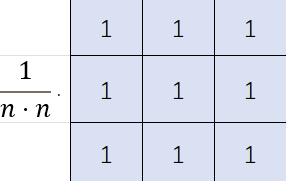
1、方框滤波器
权重分配为nxm个邻域的值之和再归一化:

opencv函数:
CV_EXPORTS_W void boxFilter( InputArray src, OutputArray dst, int ddepth,
Size ksize, Point anchor = Point(-1,-1),
bool normalize = true,
int borderType = BORDER_DEFAULT );
2、均值滤波器
CV_EXPORTS_W void blur( InputArray src, OutputArray dst,
Size ksize, Point anchor = Point(-1,-1),
int borderType = BORDER_DEFAULT );
3、高斯滤波器
高斯滤波器采用高斯距离权重的思想:
高斯分布的概率密度函数为
p ( y ) = 1 σ 2 π e − ( y − μ ) 2 2 σ 2 p(y)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(y-\mu)^2}{2\sigma^2}} p(y)=σ2π1e−2σ2(y−μ)2
其中位置参数(期望也叫均值)为μ、方差为 σ 2 \sigma^2 σ2
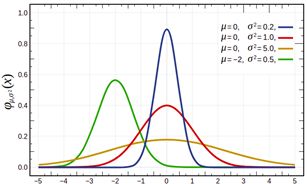
二维高斯函数为:
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} G(x,y)=2πσ21e−2σ2x2+y2
其中G(x,y)为所求像素点(x,y)在u=0条件下的概率密度,也就是权重;
大致意思为:假定当前运算点为期望值点,假设周围的像素值随距离呈正态分布。
(对当前像素点的影响随正态分布,即可通过距离求得对应高斯概率密度,即权值)
//高斯滤波核
Mat gaussi(double sigma, int ksize)
{
Mat filter_gauss = (Mat_<double>(ksize, ksize));
vector<vector<double> > f_xy(ksize, vector<double>(ksize));
double x = 0;
int center = (ksize - 1) / 2;
double C = (float)1 / (2 * CV_PI*sigma*sigma);
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
f_xy[i][j] =
C*exp(-(pow((i-center), 2) + pow((j-center), 2))/double(2 *sigma*sigma));
//高斯概率密度
x += f_xy[i][j];
filter_gauss.at<double>(i, j) = f_xy[i][j];
}
}
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
filter_gauss.at<double>(i, j) /= x;//归一化操作
}
}
return filter_gauss;
}
opencv中的函数为:
CV_EXPORTS_W void GaussianBlur( InputArray src, OutputArray dst, Size ksize,
double sigmaX, double sigmaY = 0,
int borderType = BORDER_DEFAULT );
这里说一下:
sigmaX 与 sigmaY 为两个维度的高斯标准差,我自己写的代码两个sigma相同;
三、非线性滤波器
1、中值滤波器
中值滤波器原理很简单,在掩膜范围内排序,找出中值作为当前像素点的值;
(具体的实现效果针对取中值算法的不同而不同)
中值滤波器:

逻辑运算(取中位数):
Value5 = Median{Value1,Value2,Value3,Value4,Value5,Value6,Value7,Value8,Value9}
例如:Median{4,6,5,7,8,6,9,1,5} = Median{ 1 , 4, 5, 5, 6, 6, 7, 8, 9} = 6
普通插入排序代码:
void sort(std::vector<int> &arr,int size )
{
for (int j = 1; j < size*size; j++)
{
int val = arr[j];
int n = j-1;
while (n > 0 && val <= arr[n] )
{
arr[n+1] = arr[n];
n--;
}
arr[n+1] = val;
}
}
中值滤波代码:
//中值滤波
void median(Mat src, Mat &dst, int size)
{
dst = src.clone();
for (size_t i = (size-1)/2; i < src.rows- ((size - 1) / 2); i++)
{
for (size_t j = (size - 1) / 2; j < src.cols- ((size - 1) / 2); j++)
{
vector<int> vec_0, vec_1, vec_2;
for (size_t m =0 ; m < size; m++)
{
for (size_t n = 0; n < size; n++)
{
//把每个kernel中的值存入vector中便于排序
vec_0.push_back(src.at<Vec3b>(i - ((size - 1) / 2) + m,
j - ((size - 1) / 2) + n)[0]);
vec_1.push_back(src.at<Vec3b>(i - ((size - 1) / 2) + m,
j - ((size - 1) / 2) + n)[1]);
vec_2.push_back(src.at<Vec3b>(i - ((size - 1) / 2) + m,
j - ((size - 1) / 2) + n)[2]);
}
}
sort(vec_0,size);
sort(vec_1,size);
sort(vec_2,size);
//取中值
dst.at<Vec3b>(i, j)[0] = vec_0[(pow(size, 2) - 1) / 2];
dst.at<Vec3b>(i, j)[1] = vec_1[(pow(size, 2) - 1) / 2];
dst.at<Vec3b>(i, j)[2] = vec_2[(pow(size, 2) - 1) / 2];
}
}
}
OpenCV的函数:
CV_EXPORTS_W void medianBlur( InputArray src, OutputArray dst, int ksize );
2、双边滤波器
双边滤波采用空域与频域联合权值的方法:
具体操作就是:
1、求出knernel核的空间域高斯权值;
2、求出每个点的像素值针对偏移mu(当前像素像素值)的高斯权值;
3、两个权值相乘;
第一个操作高斯滤波,由于高斯滤波会丢失图像的边缘信息,使图像边缘变得平滑,所以使用频域权值的思想来改善。

公式很简单:
就是二维高斯分布再乘上一个一维的高斯分布
W s = 1 2 π σ 2 e − ( x − u ) 2 + ( y − v ) 2 2 σ 2 Ws=\frac{1}{2\pi\sigma^2}e^{-\frac{(x-u)^2+(y-v)^2}{2\sigma^2}} Ws=2πσ21e−2σ2(x−u)2+(y−v)2
W v = 1 σ 2 π e − ( f ( x , y ) − f ( u , v ) ) 2 2 σ 2 Wv=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(f(x,y)-f(u,v))^2}{2\sigma^2}} Wv=σ2π1e−2σ2(f(x,y)−f(u,v))2
W = W s ∗ W v W = Ws*Wv W=Ws∗Wv
其中 f ( x , y ) f(x,y) f(x,y)为坐标点 ( x , y ) (x,y) (x,y)的值, ( u , v ) (u,v) (u,v)为kernel中点;
s − s p a c e , v − v a l u e s-space,v-value s−space,v−value
话不多说,上代码(一开始出了好几个bug):
//双边滤波
Mat bilateral(Mat src, int N,double sigma_gray, double sigma_space)
{
// //拷贝源图像,可以视为边缘不做处理
Mat dst;
dst = src.clone();
//值域与空间域的高斯常数
double C_gray = (float)1 / (sqrt(2 * CV_PI)*sigma_gray);//高斯常数
double C_space = (float)1 / (2 * CV_PI*sigma_space*sigma_space);
//1、空间域权值
int size = (2 * N) - 1;//N为边界距离中心的距离
int ptr_size = size;
//创建向量存储权值
vector<vector<double>> space_w(size, vector<double>(size));
//权重累积
double x_space = 0.0;
for (int i = 0 ; i < size ; i++)
{
for (int j = 0; j < size; j++)
{
space_w[i][j] = (double)C_space*exp(-(1.0 / 2 * sigma_space*sigma_space)*(pow((i - N), 2) + pow((j - N), 2)));
//获取总权值
x_space += space_w[i][j];
}
}
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
//权值归一化
space_w[i][j] /= x_space;
}
}
//2、直接计算双边滤波
//初始化指向指针数组的指针
//值域的权重
double gray_w;
//权值归一化
double x_gray = 0.0;
//建立当前行的指针
uchar **center = (uchar **)malloc(sizeof(uchar*)*(src.rows));
//每一行一个指针
for (int p = 0; p < src.rows; p++)
{
center[p] = dst.ptr<uchar>(p);
}
//N,N为高斯中心的坐标
for (int i = N ; i < src.rows-N; i++)
{
//总的列数
for (int j = N*src.channels(); j < (src.cols-N)*src.channels(); j++)
{
//获取中点像素值
int mu = center[i][j];
//space 的位置;
int index = 0;
for (int r = i - N ; r < i + N-1 ; r++)
{
for (int c = 0; c < (size-1)*src.channels(); c += src.channels())
{
//获取当前点的像素值
int gray = center[r][c];
//每个点的最终值(未归一化)
double last = 0.0;
//计算值域权值
gray_w = (double)C_gray*exp(-(1.0 / (2 * sigma_gray*sigma_gray))*pow((gray - mu), 2));
//计算总的权值
x_gray += gray_w;
last += (double)(gray_w*gray*space_w[index][(c/src.channels())%size]);
uchar center_value = saturate_cast<uchar>(center[i][j] + double(last / x_gray));
//每个点的最终值
center[i][j] = center_value;
}
//空域权值索引
index += 1;
}
}
}
return dst;
}
OpenCV的函数为:
CV_EXPORTS_W void bilateralFilter( InputArray src, OutputArray dst, int d,
double sigmaColor, double sigmaSpace,
int borderType = BORDER_DEFAULT );
针对高斯噪声的结果(sigma都为0.8):
四、代码
函数的申明和调用在前面,后面是5种滤波函数的实现;
#include