【机器学习】逻辑回归案例一：保险与年龄之间关系分析

手动反爬虫，禁止转载： 原博地址 https://blog.csdn.net/lys_828/article/details/121873835（CSDN博主：Be_melting）

 知识梳理不易，请尊重劳动成果，文章仅发布在CSDN网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

逻辑回归案例一：保险与年龄之间关系分析

1 数据加载

导入模块和加载数据

import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline

import warnings
warnings.filterwarnings('ignore')

df = pd.read_csv('../data/insurance_data.csv')
df.head()

输出结果如下。

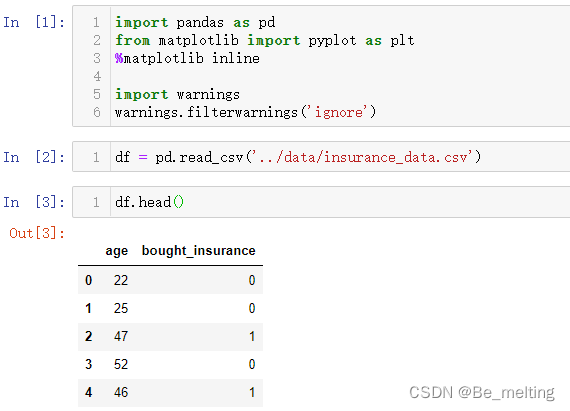
数据集中一共两个字段，第一个年龄，第二个为是购买保险的情况，购买就标记为1，未购买就标记为0。可以通过绘图查看两个字段之间的关系，代码如下。

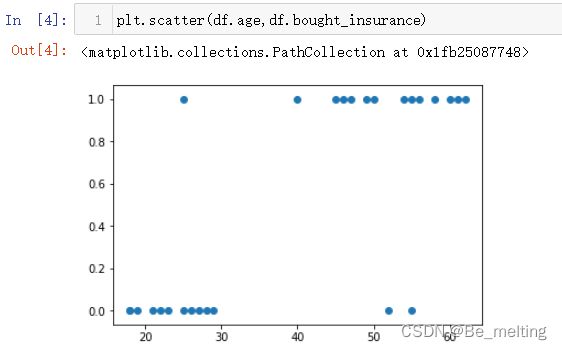
plt.scatter(df.age,df.bought_insurance)

输出结果如下。

根据图形结果，可以看出年龄在于30岁以下的人员购买保险的可能性较低，但是年龄在40岁往上的人员购买保险的人数较高。现在有一个问题：到底一个人员在多少岁是会买保险的？

假定设定为35岁，但是图中有三个异常点，左侧一个是在35岁以下买了保险，右侧两个是35岁以上却没有购买保险。此时就涉及到经常被提及的鲁棒性问题（Robost），表示 控制系统在一定(结构/大小)的参数摄动下，维持其它某些性能的特性。 也就是换成通俗的话：即使有部分问题（异常值）也不会导致系统故障。

考虑到模型的鲁棒性问题，图中三个异常数据相当于就是被忽略了，然后再进行购买保险年龄的划分貌似简单许多，但是这里划分的一条直线就相当于是指定一个x值，如果是在单次模型运行中肯定没有问题，但是在接下来运行时就会产生问题。拿考试的成绩预测来讲，考了两次数学，第一次83，第二次为87，那么第三次就预测为85猜对的可能性也不是没有，但是相较于给定一个预测区间会靠谱许多，比如预测最终的成绩在82-88之间。同理这种方式也可以应用在本次的案例中，可以给定一个范围区间，某一范围的人购买保险的概率很高，但是某一范围的人购买保险的概率很低。

2 数据切分

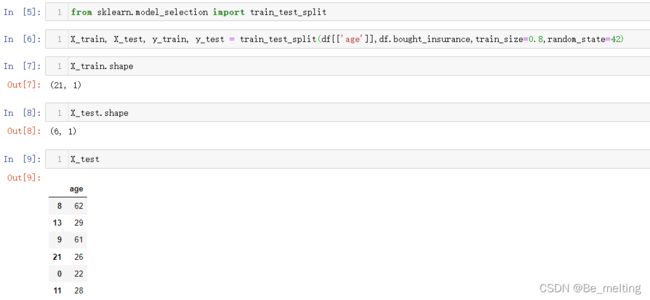
导入切分数据的函数，进行8:2切分训练集和测试集数据，代码操作如下。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df[['age']],
													df.bought_insurance,
													train_size=0.8,
													random_state=42)

X_train.shape
X_test.shape
X_test

输出结果如下。

3 模型创建与应用

导入创建模型的函数，并进行应用，具体的步骤梳理如下。

#第一步：导入创建的模型函数
from sklearn.linear_model import LogisticRegression
#第二步：模型初始化
model = LogisticRegression()
#第三步：训练模型
model.fit(X_train, y_train)
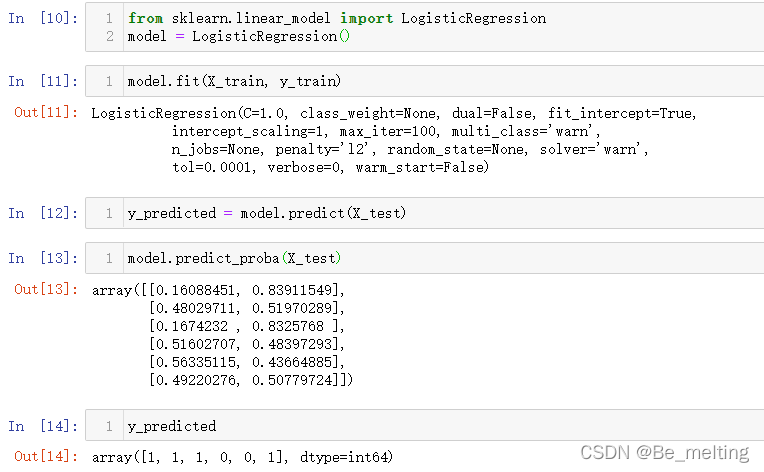
#第四步：模型预测
y_predicted = model.predict(X_test)
#第五步：输出预测概率/结果
model.predict_proba(X_test)  #输出概率
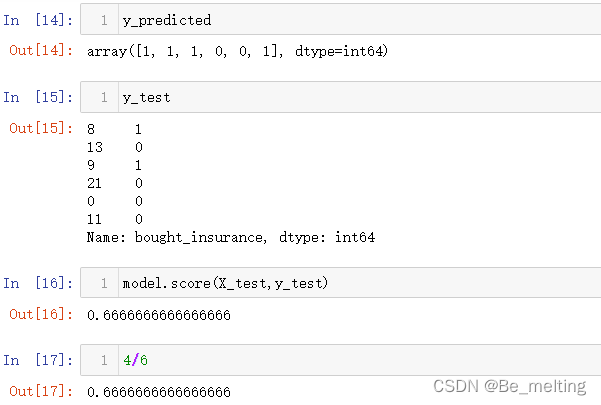
y_predicted					 #输出结果
#第六步：核实真实数据，检验的得分
y_test
model.score(X_test,y_test)

前五步的输出结果如下。

第六步的输出结果如下。

4 逻辑回归和线性回归关系

逻辑回归是基于线性回归之上的，两者均属于回归，也就是判断预测的结果接近真实值的程度，只不过逻辑回归是按照概率将预测的结果进行分类。

模型应用后可以直接输出斜率和截距，代码操作如下。

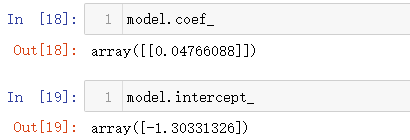
model.coef_
model.intercept_

输出结果如下。相当于最后的模型为y = 0.0477x -1.303

如果手动完成sklearn中的逻辑回归的算法，需要自己定义函数进行计算，首先通过sigmoid转化器，把直线变成s型曲线。

import math
def sigmoid(x):
    return 1 / (1 + math.exp(-x))

# y = 0.0477x -1.303
def prediction_function(age):
    z =0.0477 * age - 1.303
    y = sigmoid(z)
    return y

对应的曲线就是如下图形。

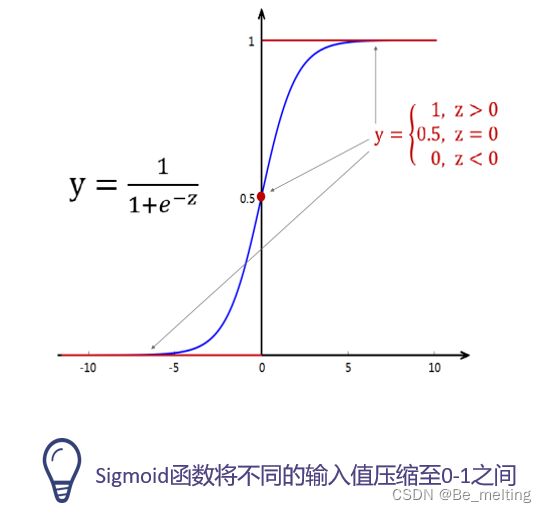
假如年龄是50岁的人，购买保险的概率计算，输出结果如下。

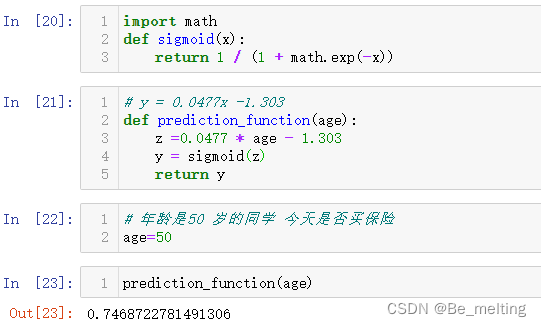
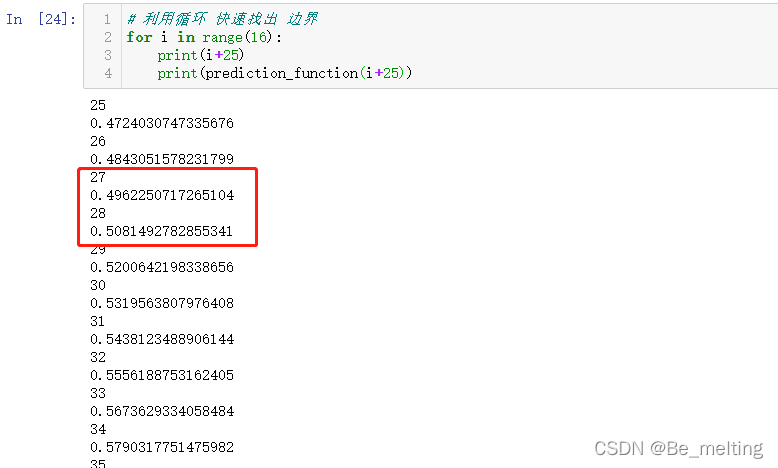
最后就是可以利用for循环快速找出边界，代码如下。

for i in range(16):
    print(i+25)
    print(prediction_function(i+25))

输出结果如下。可以看出27-28岁这个之间是作为是否购买保险的分界线（此结果和指定的随机种子有关系，当前指定的random_state的值为42）