【机器学习】6大监督学习模型:毒蘑菇分类
公众号:尤而小屋
作者:Peter
编辑:Peter
大家好,我是Peter~
本文是kaggle案例分享的第3篇,赛题的名称是:Mushroom Classification,Safe to eat or deadly poison?
数据来自UCI:https://archive.ics.uci.edu/ml/datasets/mushroom
kaggle源码地址:https://www.kaggle.com/nirajvermafcb/comparing-various-ml-models-roc-curve-comparison

排名
下面是kaggle上针对本题的排名。第一名侧重点是特征选择,没有用到本题的数据,我个人感觉跑偏了;第二名侧重点是基于贝叶斯理论的分类,能力有限,贝叶斯这块学习好了专门再说。
所以,选择了第三名的notebook源码来学习。作者将6种监督学习的方法在本数据集上的建模、模型评估等过程进行了比较。
数据集
这份数据集是UCI捐献给kaggle的。总样本数为8124,其中6513个样本做训练,1611个样本做测试;并且,其中可食用有4208样本,占51.8%;有毒的样本为3916,占48.2%。每个样本描述了蘑菇的22个属性,比如形状、气味等。
误食野生蘑菇中毒事件时有发生,且蘑菇形态千差万别,对于非专业人士,无法从外观、形态、颜色等方面区分有毒蘑菇与可食用蘑菇,没有一个简单的标准能够将有毒蘑菇和可食用蘑菇区分开来。要了解蘑菇是否可食用,必须采集具有不同特征属性的蘑菇是否有毒进行分析。
对蘑菇的22种特征属性进行分析,从而得到蘑菇可使用性模型,更好的预测出蘑菇是否可食用。
下面是UCI显示的具体数据信息:

属性特征的解释:

数据EDA
导入数据
import pandas as pd
import numpy as np
import plotly_express as px
from matplotlib import pyplot as plt
import seaborn as sns
# 忽略警告
import warnings
warnings.filterwarnings('ignore')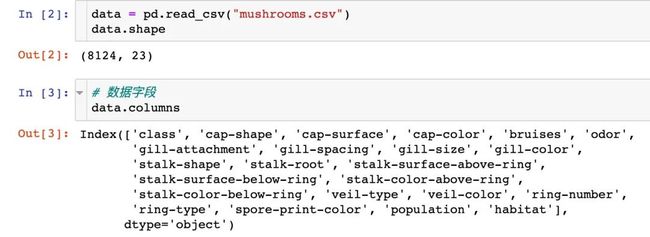
原始数据有8124条记录,23个属性;并且不存在缺失值

有无毒对比
统计有毒和无毒的数量对比:

可视化分析
菌盖颜色
首先我们讨论下菌盖的颜色:每种菌盖颜色的次数
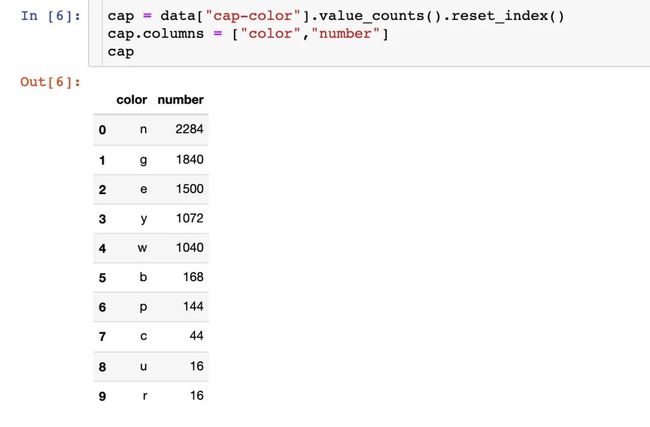
fig = px.bar(cap,x="color",
y="number",
color="number",
text="number",
color_continuous_scale="rainbow")
# fig.update_layout(text_position="outside")
fig.show()
到底有毒的蘑菇是哪几种颜色较多了?统计有毒和无毒下的颜色分布:

fig = px.bar(cap_class,x="color",
y="number",
color="class",
text="number",
barmode="group",
)
fig.show()
小结:颜色n、g、e在有毒p情况是比较多的。
菌的气味
统计每种气味的数量:
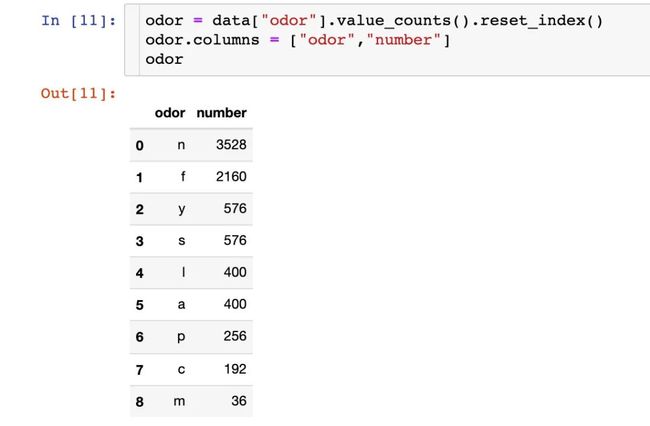
fig = px.bar(odor,
x="odor",
y="number",
color="number",
text="number",
color_continuous_scale="rainbow")
fig.show()
上面是针对整体数据的情况,下面分有毒和无毒来继续讨论:
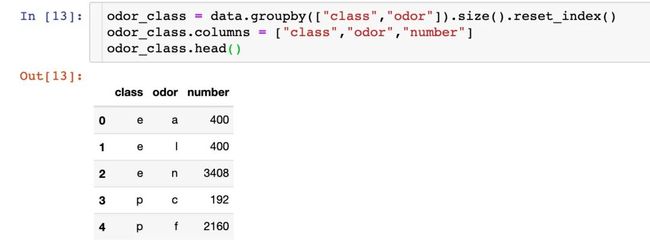
fig = px.bar(odor_class,
x="odor",
y="number",
color="class",
text="number",
barmode="group",
)
fig.show()
小结:从上面的两张图中,我们看出来:f这种气味是最容易造成有毒
特征相关性
将特征之间的相关性系数绘制成热力图,查看分布情况:
corr = data.corr()
sns.heatmap(corr)
plt.show()
特征工程
特征转换
原数据中的特征都是文本类型,我们将其转成数值型,方便后续分析:
1、转换前

2、实施转换
from sklearn.preprocessing import LabelEncoder # 类型编码
labelencoder = LabelEncoder()
for col in data.columns:
data[col] = labelencoder.fit_transform(data[col])
# 转换后
data.head()
3、查看部分属性的转换结果

数据分布
查看数据转换编码后的数据分布情况:

ax = sns.boxplot(x='class',
y='stalk-color-above-ring',
data=data)
ax = sns.stripplot(x="class",
y='stalk-color-above-ring',
data=data,
jitter=True,
edgecolor="gray")
plt.title("Class w.r.t stalkcolor above ring",fontsize=12)
plt.show()
分离特征和标签
X = data.iloc[:,1:23] # 特征
y = data.iloc[:, 0] # 标签数据标准化
# 归一化(Normalization)、标准化(Standardization)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
X
主成分分析PCA
PCA过程
原始数据中22个属性可能并不是特征都是有效数据,或者说某些属性本身就存在一定的关系,造成了特征属性的重叠。我们采用主成分分析,先找出关键的特征:
# 1、实施pca
from sklearn.decomposition import PCA
pca = PCA()
pca.fit_transform(X)
# 2、得到相关系数
covariance = pca.get_covariance()
# 3、得到每个变量对应的方差值
explained_variance=pca.explained_variance_
explained_variance
通过绘图来展示每个主成分的得分关系:
with plt.style.context("dark_background"): # 背景
plt.figure(figsize=(6,4)) # 大小
plt.bar(range(22), # 主成分个数
explained_variance, # 方差值
alpha=0.5, # 透明度
align="center",
label="individual explained variance" # 标签
)
plt.ylabel('Explained variance ratio') # 轴名称和图例
plt.xlabel('Principal components')
plt.legend(loc="best")
plt.tight_layout() # 自动调整子图参数
结论:从上面的图形中看出来最后的4个主成分方差之和很小;前面的17个占据了90%以上的方差,可作为主成分。
We can see that the last 4 components has less amount of variance of the data.The 1st 17 components retains more than 90% of the data.
2个主成分下的数据分布
然后我们利用基于2个属性的数据来实施K-means聚类:
1、2个主成分下的原始数据分布
N = data.values
pca = PCA(n_components=2)
x = pca.fit_transform(N)
plt.figure(figsize=(5,5))
plt.scatter(x[:,0],x[:,1])
plt.show()
2、实施聚类建模后的分布:
from sklearn.cluster import KMeans
km = KMeans(n_clusters=2,random_state=5)
N = data.values # numpy数组形式
X_clustered = km.fit_predict(N) # 建模结果0-1
label_color_map = {0:"g", # 分类结果只有0和1,进行打标
1:"y"}
label_color = [label_color_map[l] for l in X_clustered]
plt.figure(figsize=(5,5))
# x = pca.fit_transform(N)
plt.scatter(x[:,0],x[:,1], c=label_color)
plt.show()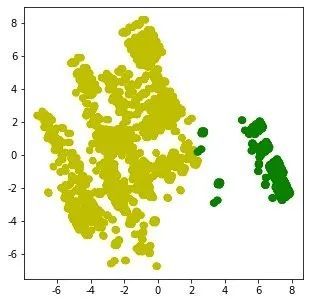
基于17主成分下的建模
这个地方自己也没有看懂:总共是22个属性,上面选取了4个特征,为什么这里是基于17个主成分的分析??
先做了基于17个主成分的转换:

数据集的划分:训练集和测试集占比为8-2
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=4)下面开始是6种监督学习方法的具体过程:
模型1:逻辑回归
from sklearn.linear_model import LogisticRegression # 逻辑回归(分类)
from sklearn.model_selection import cross_val_score # 交叉验证得分
from sklearn import metrics # 模型评价
# 建立模型
model_LR = LogisticRegression()
model_LR.fit(X_train, y_train)
查看具体的预测效果:
model_LR.score(X_test,y_pred)
# 结果
1.0 # 效果很好逻辑回归下的混淆矩阵:
confusion_matrix = metrics.confusion_matrix(y_test, y_pred)
confusion_matrix
# 结果
array([[815, 30],
[ 36, 744]])具体的auc值:
auc_roc = metrics.roc_auc_score(y_test, y_pred) # 测试纸和预测值
auc_roc
# 结果
0.9591715976331362真假阳性
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate,thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(false_positive_rate,true_positive_rate)
roc_auc
# 结果
0.9903474434835382ROC曲线
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title("ROC") # Receiver Operating Characteristic
plt.plot(false_positive_rate,
true_positive_rate,
color="red",
label="AUC = %0.2f"%roc_auc
)
plt.legend(loc="lower right")
plt.plot([0,1],[0,1],linestyle="--")
plt.axis("tight")
# 真阳性:预测类别为1的positive;预测正确True
plt.ylabel("True Positive Rate")
# 假阳性:预测类别为1的positive;预测错误False
plt.xlabel("False Positive Rate")
下面是对逻辑回归模型进行校正。这里的校正主要就是采取网格搜索的方法来选取最佳的参数,然后进行下一步的建模。网格搜索的过程:
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
from sklearn import metrics
# 未优化的模型
LR_model= LogisticRegression()
# 待确定的参数
tuned_parameters = {"C":[0.001,0.01,0.1,1,10,100,1000],
"penalty":['l1','l2'] # 选择不同的正则方式,防止过拟合
}
# 网格搜索模块
from sklearn.model_selection import GridSearchCV
# 加入网格搜索功能
LR = GridSearchCV(LR_model, tuned_parameters,cv=10)
# 搜索之后再建模
LR.fit(X_train, y_train)
# 确定参数
print(LR.best_params_)
{'C': 100, 'penalty': 'l2'}查看优化后的预测情况:

混淆矩阵和AUC情况:

ROC曲线情况:
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
#roc_auc = auc(false_positive_rate, true_positive_rate)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title("ROC") # Receiver Operating Characteristic
plt.plot(false_positive_rate,
true_positive_rate,
color="red",
label="AUC = %0.2f"%roc_auc
)
plt.legend(loc="lower right")
plt.plot([0,1],[0,1],linestyle="--")
plt.axis("tight")
# 真阳性:预测类别为1的positive;预测正确True
plt.ylabel("True Positive Rate")
# 假阳性:预测类别为1的positive;预测错误False
plt.xlabel("False Positive Rate")
模型2:高斯朴素贝叶斯
建模
from sklearn.naive_bayes import GaussianNB
model_naive = GaussianNB()
# 建模
model_naive.fit(X_train, y_train)
# 预测概率
y_prob = model_naive.predict_proba(X_test)[:,1]
y_pred = np.where(y_prob > 0.5,1,0)
model_naive.score(X_test,y_pred)
# 结果
1预测值和真实值不等的数量:111个

交叉验证
scores = cross_val_score(model_naive,
X,
y,
cv=10,
scoring="accuracy"
)
scores
混淆矩阵和AUC

真假阳性
# 导入评价模块
from sklearn.metrics import roc_curve, auc
# 评价指标
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
# roc曲线面积
roc_auc = auc(false_positive_rate, true_positive_rate)
roc_auc
# 结果
0.9592201486876043ROC曲线
AUC的值才0.96
# 绘图
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title("ROC")
plt.plot(false_positive_rate,true_positive_rate,color="red",label="AUC=%0.2f"%roc_auc)
plt.legend(loc="lower right")
plt.plot([0,1],[0,1],linestyle='--')
plt.axis("tight")
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()
模型3:支持向量机SVM
默认参数下的支持向量机过程
建模过程
from sklearn.svm import SVC
svm_model = SVC()
tuned_parameters = {
'C': [1, 10, 100,500, 1000],
'kernel': ['linear','rbf'],
'C': [1, 10, 100,500, 1000],
'gamma': [1,0.1,0.01,0.001, 0.0001],
'kernel': ['rbf']
}随机网格搜索-RandomizedSearchCV
from sklearn.model_selection import RandomizedSearchCV
# 建立随机搜索模型
model_svm = RandomizedSearchCV(
svm_model, # 待搜索模型
tuned_parameters, # 参数
cv=10, # 10折交叉验证
scoring="accuracy", # 评分标准
n_iter=20 # 迭代次数
)
# 训练模型
model_svm.fit(X_train,y_train)RandomizedSearchCV(cv=10,
estimator=SVC(),
n_iter=20,
param_distributions={'C': [1, 10, 100, 500, 1000],
'gamma': [1, 0.1, 0.01, 0.001, 0.0001],
'kernel': ['rbf']},
scoring='accuracy')# 最佳得分效果
print(model_svm.best_score_)
1.0得分最佳匹配参数:

# 预测
y_pred = model_svm.predict(X_test)
# 预测值和原始标签值计算:分类准确率
metrics.accuracy_score(y_pred, y_test)
# 结果
1混淆矩阵
查看具体的混淆矩阵和预测情况:

ROC曲线
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_pred)
roc_auc = auc(false_positive_rate, true_positive_rate)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title('ROC')
plt.plot(false_positive_rate,true_positive_rate, color='red',label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],linestyle='--')
plt.axis('tight')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
模型5:随机森林
建模拟合
from sklearn.ensemble import RandomForestClassifier
# 建模
model_RR = RandomForestClassifier()
# 拟合
model_RR.fit(X_train, y_train)预测得分

混淆矩阵

ROC曲线
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(false_positive_rate, true_positive_rate)
roc_auc # 1
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title('ROC')
plt.plot(false_positive_rate,true_positive_rate, color='red',label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],linestyle='--')
plt.axis('tight')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()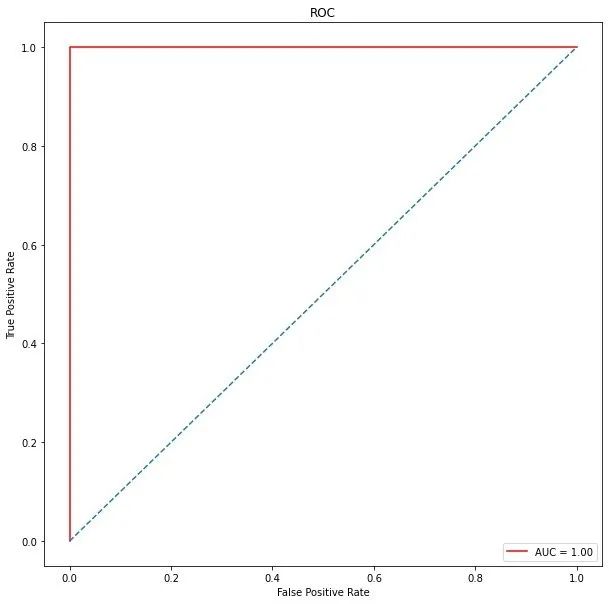
模型6:决策树(CART)
建模
from sklearn.tree import DecisionTreeClassifier
# 建模
model_tree = DecisionTreeClassifier()
model_tree.fit(X_train, y_train)
# 预测
y_prob = model_tree.predict_proba(X_test)[:,1]
# 预测的概率转成0-1分类
y_pred = np.where(y_prob > 0.5, 1, 0)
model_tree.score(X_test, y_pred)
# 结果
1混淆矩阵
各种评价指标的体现:

ROC曲线
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(false_positive_rate, true_positive_rate)
roc_auc # 1
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10)) # 画布
plt.title('ROC') # 标题
plt.plot(false_positive_rate, # 绘图
true_positive_rate,
color='red',
label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right') # 图例位置
plt.plot([0, 1], [0, 1],linestyle='--') # 正比例直线
plt.axis('tight')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()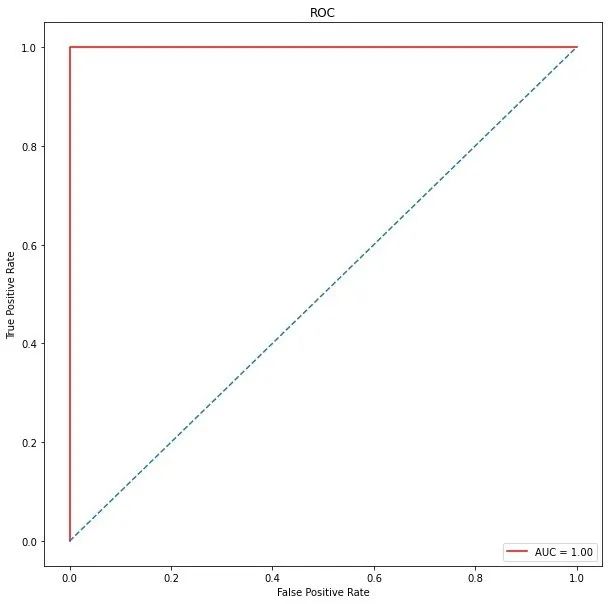
模型6:神经网络ANN
建模

混淆矩阵

ROC曲线
# 真假阳性
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(false_positive_rate, true_positive_rate)
roc_auc # 1
# 绘制ROC曲线
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title('ROC')
plt.plot(false_positive_rate,true_positive_rate, color='red',label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],linestyle='--')
plt.axis('tight')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
下面对神经网络的参数进行调优:
hidden_layer_sizes:隐藏层个数
activation:激活函数
alpha:学习率
max_iter:最大迭代次数
网格搜索
from sklearn.neural_network import MLPClassifier
# 实例化
mlp_model = MLPClassifier()
# 待调节参数
tuned_parameters={'hidden_layer_sizes': range(1,200,10),
'activation': ['tanh','logistic','relu'],
'alpha':[0.0001,0.001,0.01,0.1,1,10],
'max_iter': range(50,200,50)
}
model_mlp= RandomizedSearchCV(mlp_model,
tuned_parameters,
cv=10,
scoring='accuracy',
n_iter=5,
n_jobs= -1,
random_state=5)
model_mlp.fit(X_train,y_train)
模型属性
调优之后的模型属性情况以及合适的参数:

ROC曲线
from sklearn.metrics import roc_curve, auc
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(false_positive_rate, true_positive_rate)
roc_auc # 1
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.title('ROC')
plt.plot(false_positive_rate,true_positive_rate, color='red',label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],linestyle='--')
plt.axis('tight')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
混淆矩阵和ROC
这是一篇很好的文章来解释混淆矩阵和ROC:https://www.cnblogs.com/wuliytTaotao/p/9285227.html
1、什么是混淆矩阵?

2、4大指标
TP、FP、TN、FN,第二个字母表示样本被预测的类别,第一个字母表示样本的预测类别与真实类别是否一致。

3、准确率

4、精准率和召回率

5、F_1和F_B


6、ROC曲线
AUC全称为Area Under Curve,表示一条曲线下面的面积,ROC曲线的AUC值可以用来对模型进行评价。ROC曲线如图 1 所示:

总结
看完这篇notebook源码,你需要掌握的知识点:
机器学习建模整体思路:选择模型、建模、网格搜索调参、模型评估、ROC曲线(分类)
特征工程的技术:编码转换、数据标准化、数据集划分
评价指标:混淆矩阵、ROC曲线作为重点,后续有文章专门讲解
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件本站qq群955171419,加入微信群请扫码:
