python实现时间序列分析1:传统时间序列分析法
本文将针对时间序列方法的python实现进行系统的介绍。
文章目录
- 1 移动平均法系列
-
- 1.1 朴素预测法
- 1.2 简单移动平均法
- 1.3 加权移动平均法
- 1.4 指数平滑法
- 2 传统时间序列分析方法
-
- 2.1 ARIMA
- 2.2 Holt
- 2.3 灰色预测
- 3 传统机器学习方法(以xgboost为例)
- 4 总结
1 移动平均法系列
移动平均法是指在当前时间添加时间窗口,取窗口内平均值,或者加权平均值。
1.1 朴素预测法
朴素预测法是指直接使用前一时刻的时序值作为后一个时刻的预测值。
1.2 简单移动平均法
#读取数据
import pandas as pd
data = pd.read_excel("data.xlsx")
print("=================INFO=============")
print(data.info())
X = data[["f1","f2"]]
Y = data["target"]
X_train = X[0:17]
Y_train = Y[0:17]
print("=================DATA==============")
data.head()
#简单移动平均
import matplotlib.pyplot as plt
def ma(time_s_part):
n = len(time_s_part)
sum = 0
for i in time_s_part:
sum += i
result = sum / n
return result
def answer1(time_s, n):
"""
两个参数:
time_s:时间序列
n:移动的步长,即移动的期数
"""
result_ma = [] # 简单移动平均值的列表
for i in range(n - 1, len(time_s)):
time_s_part = (time_s[i - (n - 1):i + 1])
result_ma.append(ma(time_s_part))
print("Result of moving average:{}".format(result_ma))
x = result_ma[-1]
print("Prediction value:{}".format(x))
# 可视化
plt.scatter(list(range(len(result_ma))), result_ma)
plt.show()
if __name__ == '__main__':
n = 3
answer1(Y_train, n)
1.3 加权移动平均法
在简单移动平均的基础上对每一期的数据添加权重。
import matplotlib.pyplot as plt
# 加权移动平均法
def wma(list2, w):
n = len(list2)
sum = 0
for i in n:
sum += list2[i] * w[i]
return sum
def answer2(list1, n):
# 加权移动平均法
w = [0.2, 0.3, 0.5] # 各期的权重
listWMA = [] # 加权移动平均值的列表
for i in range(n - 1, len(list1)):
list2 = (list1[i - (n - 1):i + 1])
listWMA.append(ma(list2))
print("加权移动平均值的列表:{}".format(listWMA))
# 最后的移动平均值可做为下一个数的预测
x = listWMA[-1]
print("下一个数的预测:{}".format(x))
plt.scatter(list(range(len(listWMA))), listWMA)
plt.show()
if __name__ == '__main__':
n = 3 # 移动平均期数
answer2(Y_train, n) # 加权移动平均法
1.4 指数平滑法
指数平滑法实际上是一种特殊的加权移动平均法。其特点是: 第一,指数平滑法进一步加强了观察期近期观察值对预测值的作用,对不同时间的观察值所赋予的权数不等,从而加大了近期观察值的权数,使预测值能够迅速反映市场实际的变化。权数之间按等比级数减少,此级数之首项为平滑常数a,公比为(1- a)。第二,指数平滑法对于观察值所赋予的权数有伸缩性,可以取不同的a 值以改变权数的变化速率。如a取小值,则权数变化较迅速,观察值的新近变化趋势较能迅速反映于指数移动平均值中。因此,运用指数平滑法,可以选择不同的a 值来调节时间序列观察值的均匀程度(即趋势变化的平稳程度)。【来自百度百科】
import matplotlib.pyplot as plt
# 一次指数平滑预测
def es1(list3, t, a):
if t == 0:
return list3[0] # 初始的平滑值取实际值
return a * list3[t - 1] + (1 - a) * es1(list3, t - 1, a) # 递归调用 t-1 → 12
# 二次指数平滑预测
def es2(list3, t, a):
if t == 0:
return list3[0]
return (a * es2(list3, t - 1, a) + (1 - a) * list3[t - 1])
def answer3(list2):
# 指数平滑法
a = 0.8 # 平滑常数
listES = [] # 指数平滑值的列表
for i in range(len(list2)):
if i == 0:
listES.append(list2[i])
continue
s = a * list2[i] + (1 - a) * listES[-1]
listES.append(s)
print("指数平滑值的列表:{}".format(listES))
# 画图
plt.scatter(list(range(len(listES))), listES)
plt.show()
# 一次指数平滑预测
t = len(list2) # 预测的时期 13
x = es1(list2, t, a)
print("下一个数的一次指数平滑预测:{}".format(x))
# 二次指数平滑预测
m = 3 # 预测的值为之后的第m个
yt = es2(list2, t - 1, a)
ytm = listES[t - 2]
esm = ((2 * ytm - yt) + m * (ytm - yt) * a / (1 - a))
print("之后的第{}个数的二次指数平滑预测:{}".format(m, esm))
if __name__ == '__main__':
n = 3 # 移动平均期数
answer3(Y_train) # 指数平滑法
2 传统时间序列分析方法
本部分以经典时间序列分析方法ARIMA和Holt为例,并添加灰色预测法。
2.1 ARIMA
from __future__ import print_function
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot
import itertools
import itertools
from statsmodels.tsa.arima_model import ARIMA
p=q=range(0,2)
d = range(0,2)
print("p=",p,"d=",d,"q=",q)
pdq=list(itertools.product(p,d,q))
print("pdq:\n",pdq)
seasonal_pdq=[(x[0],x[1],x[2],12) for x in pdq]
print('SQRIMAX:{} x {}'.format(pdq[1],seasonal_pdq[1]))
#根据AIC值确定最佳参数,AIC越小越好
for param in pdq:
for param_seasonal in seasonal_pdq:
mod = sm.tsa.statespace.SARIMAX(Y_train,order=param,seasonal_order=param_seasonal,enforce_stationarity=False,enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{}1 - AIC:{}'.format(param, param_seasonal, results.aic))
#根据上述确定参数建模
Y_train = Y[0:17].tolist()
param = (1,1,1)
param_seasonal = (1, 0, 1, 12)
mod = sm.tsa.statespace.SARIMAX(Y_train,order=param,seasonal_order=param_seasonal,enforce_stationarity=False,enforce_invertibility=False)
results = mod.fit()
Y_predict = results.forecast(6)
print(Y_predict)
for item in Y_predict:
Y_train.append(item)
print(Y_train)
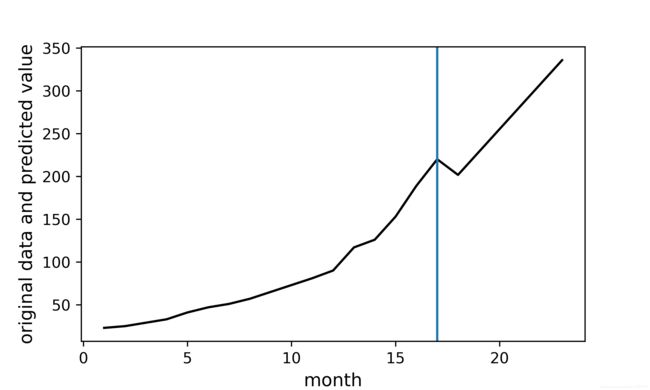
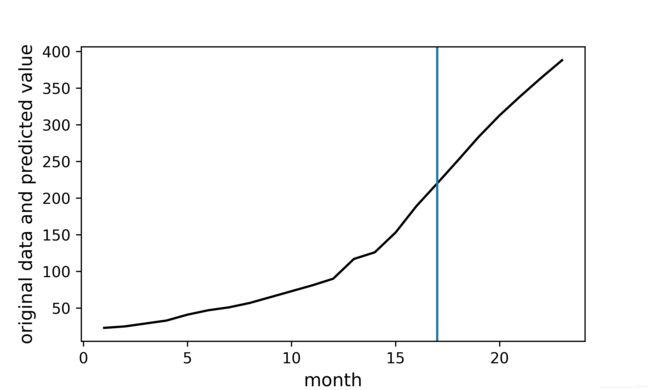
plt.figure(figsize=(6,3.6),facecolor='white',edgecolor='#ffffcc')
plt.subplot(111, facecolor='white')
plt.plot([x for x in range(1,24)],Y_train,color = "black")
plt.axvline(17)
plt.xlabel("month",color='black',fontsize = 12)
plt.ylabel("original data and predicted value",color = "black",fontsize = 12)
plt.savefig('Arima.png',dpi=600)
plt.show()
以下为可视化的结果,蓝色竖线前边是真实数据,后边是预测数据。
2.2 Holt
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.api import ExponentialSmoothing
import matplotlib.pyplot as plt
import matplotlib as mpl
import itertools
import warnings
import numpy as np
from statsmodels.tsa.api import Holt
#训练集
#模型应用
Y_train = Y[0:17]
Y_train = Y_train.tolist()
fit = Holt(np.asarray(Y_train)).fit(smoothing_level=0.1, smoothing_slope=1)
#向后预测三个值
Y_predict = fit.forecast(6)
print(Y_predict)
for item in Y_predict:
Y_train.append(item)
plt.figure(figsize=(6,3.6),facecolor='white',edgecolor='#ffffcc')
plt.subplot(111, facecolor='white')
plt.plot([x for x in range(1,24)],Y_train,color = "black")
plt.axvline(17)
plt.xlabel("month",color='black',fontsize = 12)
plt.ylabel("original data and predicted value",color = "black",fontsize = 12)
plt.savefig('Holt.png',dpi=600)
plt.show()
2.3 灰色预测
import numpy as np
import matplotlib.pyplot as plt
# 导入时间序列
Y_train = Y[0:17]
Y_train = Y_train.tolist()
lan = []
for i in range(len(Y_train)):
if i == len(Y_train) - 1:
continue
# 求级比
lan.append(Y_train[i] / Y_train[i + 1])
Y_train_1 = np.cumsum(Y_train)
# 构造数据矩阵B及数据向量
B = np.array([-1 / 2 * (Y_train_1[i] + Y_train_1[i + 1]) for i in range(len(Y_train) - 1)])
B = np.mat(np.vstack((B, np.ones((len(Y_train) - 1,)))).T)
Y_2 = np.mat([Y_train[i + 1] for i in range(len(Y_train) - 1)]).T
u = np.dot(np.dot(B.T.dot(B).I, B.T), Y_2)
[a, b] = [u[0, 0], u[1, 0]]
a_new, b = Y_train[0] - b / a, b / a
# 输入需要预测的期数
t = 6
t += len(Y_train)
Y_predict = [Y_train[0]]
Y_predict = Y_predict + [a_new * (np.exp(-a * i) - np.exp(-a * (i - 1))) for i in range(1, t)]
#计算相对误差,如果较小,则可以使用
print((np.array(Y_predict[:len(Y_train)])-np.array(Y_train[:len(Y_train)]))/np.array(Y_train[:len(Y_train)]))
print(Y_predict[len(Y_train):])
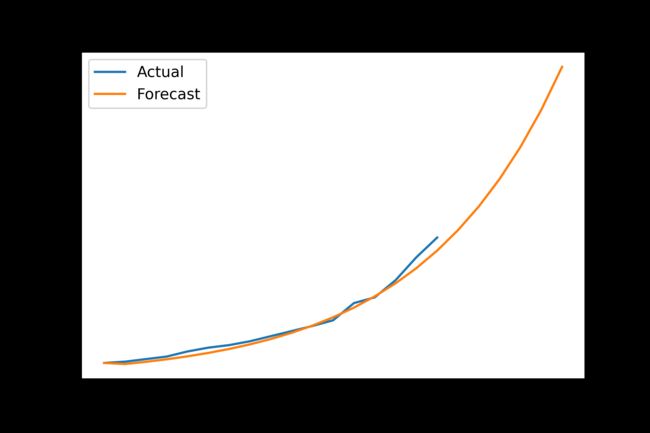
plt.plot(range(1,18),Y_train[:len(Y_train)],range(1,24),Y_predict)
plt.xlabel('Years')
plt.ylabel('Concentration [mt]')
plt.legend(['Actual','Forecast'])
plt.savefig('huise.png',dpi=600)
print(Y_predict)
3 传统机器学习方法(以xgboost为例)
工业上常用的机器学习方法为 xgboost,实践来看,根据数据特征的不同,不同集成学习方法的表现不一,如果有分类变量,可能是catboost效率和准确率更高,此处以xgboost为例。
import xgboost as xgb
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.metrics import median_absolute_error
from sklearn import metrics
from sklearn.metrics import r2_score
def apply_xgb(X_train,Y_train,X_test):
model = xgb.XGBRegressor(max_depth=5, learning_rate=0.1, n_estimators=10, silent=True, objective='reg:gamma')
model.fit(X_train, Y_train)
Y_train_predict = model.predict(X_train)
predicted_values = model.predict(X_test)
mse = mean_squared_error(Y_train,Y_train_predict)
r2 = r2_score(Y_train,Y_train_predict)
rmse = metrics.mean_squared_log_error(Y_train, Y_train_predict)
mae = median_absolute_error(Y_train, Y_train_predict)
return [predicted_values,mse,r2,rmse,mae]
data = pd.read_excel("data.xlsx")
X = data[["f1","f2"]]
Y = data["target"]
Y_train = Y[0:17]
X_train = X[0:17]
X_test = X[17:]
Y = data["target"]
Y_train = Y[0:17].tolist()
Y_predict = apply_xgb(X_train,Y_train,X_test)
print(Y_predict)
for item in (Y_predict[0].tolist()):
Y_train.append(item)
4 总结
以上就是时间序列分析的第一部分,是比较简单和传统的方法,还有第四部分和第五部分,我们要单独介绍一下深度学习和Facebook的开源时间序列分析模型Prophet。
参考链接: https://blog.csdn.net/tz_zs/article/details/78341306 赵卫东,复旦大学,TensorFlow 入门实操课程,type=detail&id=1239961119&sm=1 https://blog.csdn.net/qushoushi0594/article/details/80096213 https://baike.baidu.com/item/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95/8726217?fr=aladdin