YOLOv3详解

---

前言

yolo算法是一种one-stage的目标检测算法，与two-stage目标检测算法最大区别在于运算速度上，YOLO系列算法将图片划分成若干个网格，再基于anchor机制生成先验框，只用一步就生成检测框，这种方法大大提升了算法的预测速度，今天我们主要学习的是YOLOv3算法的主要实现过程，YOLOv3的论文于2018年发表在CVPR上.

​​论文名称：YOLOv3: An Incremental Improvement

论文下载地址: https://arxiv.org/abs/1804.02767

一、YOLOv3网络模型分析

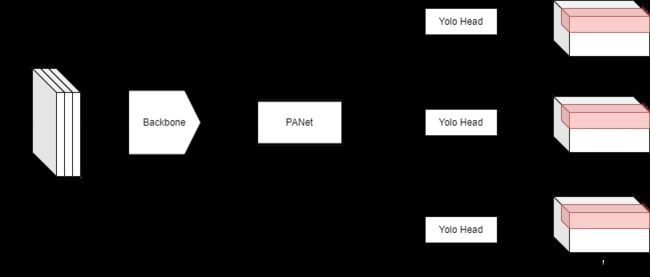
YOLOv3网络结构大致可分为三个部分：Backbone，PANet，Yolo Head,在YOLOv3-SPP结构中还引入了SPP结构，但与SPPnet的SPP略有不同。

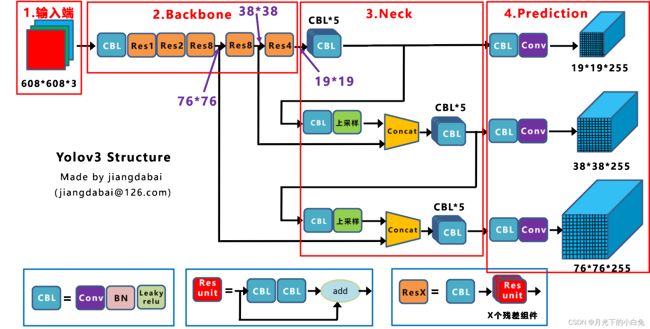
1.Backbone： Darknet-53

首先了解一下yolov3的backbone部分,Darknet-53主体与resnet结构相似，堆叠了多个 残差模块，残差模块之间间隔了一个kernel_size=3x3，stride=2卷积层，作用主要是downsample，53代表了整个backbone一共有52个卷积层和最后的connect层（全连接层），一共53层结构,下图是以输入图像256 x 256进行预训练来进行介绍的，常用的尺寸是416 x 416，都是32的倍数(经过stride后会变换特征图大小一共有5次，每次都是2倍所以确定img_size大小要是$2^5=32$)。
卷积的strides默认为1，padding默认为same(补全)，当strides为2时padding为valid（丢弃）.

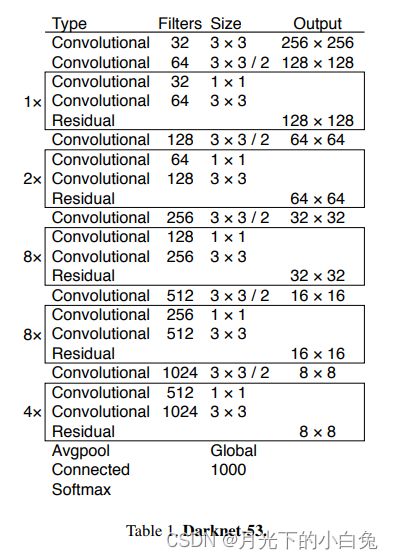
第一个3x3的卷积核主要用来增加通道数，在不改变图片尺寸的条件下获得更多的有效特征图，同时扩大特征图感受野，第二个3x3的卷积核stride=2主要作用是downsample,减少计算过程中的参数量与计算量，再堆叠多个residual block，最后对得到的feature map进行平均池化。
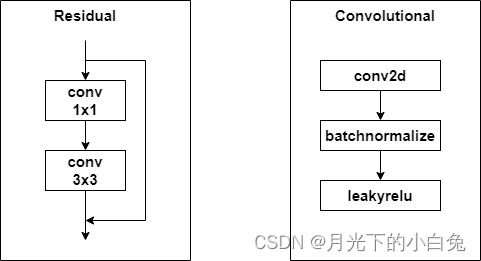
以上的Residual模块的残差连接方式与Resnet基本相同,输入特征图与输出特征图中间经过卷积核大小为1x1和3x3大小的两次卷积，再将输出的两个特征图add,Convolutional模块=conv+bn+leakrelu,如下图所示：

2.PANet

PANet对应Neck模块，是FPN的改进版本，FPN主要方法是自顶向下对浅层大尺度特征图进行下采样与深层特征图进行特征融合，输出多个不同尺度的特征图进行预测，PANet在此基础之上增加了对深层特征图的上采样操作，将深层小尺度特征图上采样后concat在一起，提出了一种自顶向下+自底向上的特征融合方式。
PANet可以被看作一个Multiple-input-multiple-output encoder.它对网络性能影响最大的主要有两个方面：
(1) 多尺度特征融合.
(2) 分而治之：简而言之就是输出多个不同尺度具有不同感受野特征图.
对于这两个影响因素谁更重要，可以参考论文YOLOF(You Only Look One-level Feature ),该论文针对提出了一种single-input-single-output的encoder，通过在残差模块中堆叠膨胀卷积使得单级特征图具有更大的感受野，在保证精度的前提下减少了encoder的参数量.

3.Yolo Head

Yolo Head是一种decoder，它的主要结构是一个conv+bn+act模块与一个kernel_size =1x1卷积分类层，用1x1卷积代替全连接层进行分类的主要原因有两点：
(1) 全连接层输入尺度被限定，而卷积层只用限定输入和输出channel
(2)全连接层输出是一维或二维，特征图输入到全连接层时需要对其进行Flatten,这样在一定程度上破环了特征图的空间信息,而卷积层输出为三维(c,w,h)，选择卷积层作为decoder,极大保留了特征图上对应原图的空间结构信息,如下图所示：
更便于匹配到正样本时，输出空间上对应的channel的值.

二、anchor网格偏移量预测

由前一部分的讲解可知，Yolo Head输出是三维的w,h 的每一个点对应原图划分的网格，channel对应的是该anchor的预测值，那我们如何计算anchor的具体位置呢？
yolo的思想是将一张图片划分为W*W个网格,每一个网格负责中心点落在该网格的目标.每个网格可以看作一个感兴趣区域，既然是区域，就需要计算预测anchor的具体坐标与bbox的w和h.
$channel=t_x+t_y+t_w+t_h+obj+nu{m}_{classes}$
其中预测值tx,ty并不是anchor的坐标，而是anchor的偏移量，同样的$t_w,t_h$是先验框的缩放因子，先验框的大小由k-means聚类xml标签文件中保存的坐标位置得到，每一个anchor有三个不同大小的先验框，预测层Yolohead有三个,总共的先验框数量为划分总网格数的三倍.

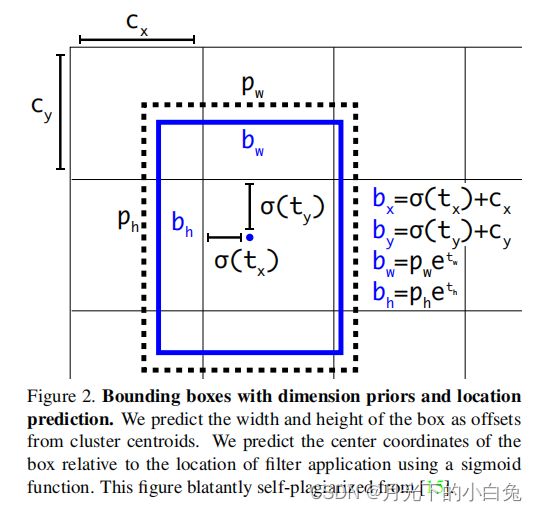
上图表示了bbox的回归过程$c_x,c_y$是网格左上角坐标,anchor向右下方偏移,为了防止anchor偏移量超出网格导致定位精度损失过高，yolov3使用了sigmoid函数将预测值tx,ty进行限制到[0,1](可以加速网络的收敛),最后得出anchor的预测坐标$b_x,b_y$.bbox的w与h由预测缩放因子$t_w与t_h$决定,$p_w和p_h$为anchor模板映射到特征图上的宽和高,通过指数函数对$t_w$与$t_h$进行放大在分别与$p_w和p_h$相乘就得到了最终预测的w和h.
PS:此处的x,y坐标点都是anchor映射到特征图的值，并不是原图上的坐标，在plot bbox应该将其转换到真实图片上的坐标再进行绘制.

三、正负样本匹配规则

在yolov3论文中提到正负样本的匹配规则是:给每一个groundtrue box分配一个正样本，这个正样本是所有bbox中找一个与gt_box的重叠区域最大的一个预测框，也就是和该gt_box的iou最大的预测框.但是如果利用这个规则去寻找正样本，正样本的数量是很少的，这将使得网络难以训练.如果一个样本不是正样本，那么它既没有定位损失，也没有类别损失，只有置信度损失，在yolov3的论文中作者尝试用focal loss来缓解正负样本不均匀的问题，但是并没有取得很好的效果，原因就在于负样本值参与了置信度损失，对loss的影响占比很小.
所以我们要去看作者在源码中是如何匹配正样本的.
源码中定义了build_targets函数来匹配正样本.

def build_targets(p, targets, model):
    """
    Build targets for compute_loss(), input targets(image,class,x,y,w,h)
    :param p: 预测框 由模型构建中的yolo_out返回的三个yolo层的输出
              tensor格式 list列表 存放三个tensor 对应的是三个yolo层的输出
              例如：[4, 3, 23, 23, 25]  [4, 3, 46, 46, 25]  [4, 3, 96, 96, 25]  (736x736尺度下)
              [batch_size, anchor_num, grid, grid, xywh + obj + classes]
              p[i].shape
    :param targets: 数据增强后一个batch的真实框 [21, 6] 21: num_object  6: batch中第几张图（0,1,2,3）+类别+x+y+w+h真实框
    :param model: 初始化的模型
    :return: tbox: append [m(正样本个数), x偏移量(中心点坐标相对中心所在grid_cell左上角的偏移量) + y偏移量 + w + h]
                   存放着当前batch中所有anchor的正样本 某个anchor的正样本指的是当前的target由这个anchor预测
                   另外，同一个target可能由多个anchor预测，所以通常 m>nt
             indices: append [m(正样本个数), b + a + gj + gi]
                   b: 和tbox一一对应 存放着tbox中对应位置的target（第a个anchor的正样本）属于这个batch中的哪一张图片
                   a: 和tbox一一对应 存放着tbox中对应位置的target是属于哪个anchor(index)的正样本（由哪个anchor负责预测）
                   gj: 和tbox一一对应 存放着tbox中对应位置的target的中心点所在grid_cell的左上角的y坐标
                   gi: 和tbox一一对应 存放着tbox中对应位置的target（第a个anchor的正样本）的中心点所在grid_cell的左上角的x坐标
             tcls: append [m] 和tbox一一对应 存放着tbox中对应位置的target（第a个anchor的正样本）所属的类别
             anch: append [m, 2] 和tbox一一对应 存放着tbox中对应位置的target是属于哪个anchor(shape)的正样本（由哪个anchor负责预测）
    """

    nt = targets.shape[0]  # 当前batch真实框的数量 num of target

    # 定义一些变量
    # anch append [m, 2] 和tbox一一对应 存放着对应位置的target是属于哪个anchor(shape)的正样本（由哪个anchor负责预测）
    tcls, tbox, indices, anch = [], [], [], []
    gain = torch.ones(6, device=targets.device)  # normalized to gridspace gain tensor([1,1,1,1,1,1])

    multi_gpu = type(model) in (nn.parallel.DataParallel, nn.parallel.DistributedDataParallel)  # 一般False
    for i, j in enumerate(model.yolo_layers):  # [89, 101, 113]  i,j = 0, 89   1, 101   2, 113
        # 获取该yolo predictor对应的anchors的大小，不过这里是缩放到feature map上的  shape=[3, 2]
        # 而且它就是cfg文件中的anchors除以了缩放比例stride得到的
        # 比如：[3.6250, 2.8125] / 13 * 416 （缩放比例为32）= [116,90]  等于cfg文件中的anchor的大小
        anchors = model.module.module_list[j].anchor_vec if multi_gpu else model.module_list[j].anchor_vec

        # gain中存放的是feature map的尺寸信息
        # 在原图尺度为(736,736)情况下  p[0]=[4,3,23,23,25] p[1]=[4,3,46,46,25] p[2]=[4,3,92,92,25]
        # 如原图(736x736)  gain=Tensor([1,1,23,23,23,23]) 或 Tensor([1,1,46,46,46,46]) 或 Tensor([1,1,92,92,92,92])
        gain[2:] = torch.tensor(p[i].shape)[[3, 2, 3, 2]]  # xyxy gain

        na = anchors.shape[0]  # number of anchors  3个
        # [3] -> [3, 1] -> [3, nt]
        # anchor tensor, same as .repeat_interleave(nt)   at.shape=[3,21] 21个0, 1, 2
        at = torch.arange(na).view(na, 1).repeat(1, nt)

        # Match targets to anchors
        # t = targets * gain: 将box坐标（在box标签生成中，对box坐标进行了归一化，即除以图像的宽高）转换到当前yolo层输出的特征图上
        #                     通过将归一化的box乘以特征图尺度，从而将box坐标投影到特征图上
        # 广播原理 targets=[21,6]  gain=[6] => gain=[6,6] => t=[21,6]
        a, t, offsets = [], targets * gain, 0

        if nt:  # 如果存在target的话
            # 把yolo层的anchor在该feature map上对应的wh（anchors）和所有预测真实框在该feature map上对应的wh(t[4:6])做iou,
            #       若大于model.hyp['iou_t']=0.2, 则为正样本保留，否则则为负样本舍弃
            # anchors: [3, 2]: 当前yolO层的三个anchor(且都是相对416x416的, 不过初始框的wh多大都可以，反正最后都是做回归)
            # t[:, 4:6]: [nt, 2]: 所有target真是框的w和h, 且都是相对当前feature map的
            # j: [3, nt]
            j = wh_iou(anchors, t[:, 4:6]) > model.hyp['iou_t']  # iou(3,n) = wh_iou(anchors(3,2), gwh(n,2))
            # t.repeat(na, 1, 1): [nt, 6] -> [3, nt, 6]
            # 获取iou大于阈值的anchor与target对应信息
            # a=tensor[30]: anchor_index(0、1、2)  0表示是属于第一个anchor(包含4张图片)的正样本  同理第二。。。
            #               再解释下什么是正样本: 表示当前target可以由第i个anchor检测，就表示当前target是这个anchor的正样本
            # t=tensor[30,6]: 第0、1、2、3(4张图片)的target, class, x, y, w, h(相对于当前feature map尺度)
            #                 与a变量一一对应，a用来指示t中相对应的位置的target是属于哪一个anchor的正样本
            #                 注意：这里的同一个target是可能会同属于多个anchor的正样本的，由多个anchor计算同一个target
            #                      不然t个数也不会大于正样本数（30>21）
            a, t = at[j], t.repeat(na, 1, 1)[j]  # filter 选出所有anchor对应属于它们的正样本

        # Define
        # b: 对应图片的index 即当前target是属于哪张图片的
        # c: 当前target是属于哪个类
        # long等于to(torch.int64), 数值向下取整  这里都是整数，long()只起到了float->int的作用
        b, c = t[:, :2].long().T  # image, class

        gxy = t[:, 2:4]  # grid xy  对应于当前feature map的target的xy坐标
        gwh = t[:, 4:6]  # grid wh  对应于当前feature map的target的wh坐标

        # 匹配targets所在的grid cell左上角坐标
        # (gxy-0).long 向下取整  得到当前target的中心点所在左上角的坐标
        gij = (gxy - offsets).long()
        # grid xy indices 左上角x, y坐标
        gi, gj = gij.T

        # Append
        indices.append((b, a, gj, gi))  # image index, anchor, grid indices(x, y)
        tbox.append(torch.cat((gxy - gij, gwh), 1))  # gt box相对当前feature map的x,y偏移量以及w,h
        anch.append(anchors[a])  # anchors
        tcls.append(c)  # class

        if c.shape[0]:  # if any targets
            # 目标的标签数值不能大于给定的目标类别数
            assert c.max() < model.nc, 'Model accepts %g classes labeled from 0-%g, however you labelled a class %g. ' \
                                       'See https://github.com/ultralytics/yolov3/wiki/Train-Custom-Data' % (
                                           model.nc, model.nc - 1, c.max())
    return tcls, tbox, indices, anch


# 这里是根据宽高（左上角对齐）来进行iou计算处理
# 与普通的IoU，GIoU，那些不一样
def wh_iou(wh1, wh2):
    """
    把yolo层的anchor在该feature map上对应的wh（anchors）和所有预测真实框在该feature map上对应的wh(t[4:6])做iou,
    若大于model.hyp['iou_t']=0.2, 则为正样本保留，否则则为负样本舍弃  筛选出符合该yolo层对应的正样本
    Args:
        wh1: anchors  [3, 2]
        wh2: target   [22,2]
    Returns:
        wh1 和 wh2 的iou [3, 22]
    """
    # Returns the nxm IoU matrix. wh1 is nx2, wh2 is mx2
    wh1 = wh1[:, None]  # [N,1,2]  [3, 1, 2]
    wh2 = wh2[None]  # [1,M,2]     [1, 22, 2]
    inter = torch.min(wh1, wh2).prod(2)  # [N,M]  [3, 22]
    return inter / (wh1.prod(2) + wh2.prod(2) - inter)  # iou = inter / (area1 + area2 - inter)

通过对上面源码的阅读我们可以得出作者首先将bbox与gr_box的左上角对齐，再计算出存在目标的anchor的bbox与gr_box的iou,并设定一个iou阈值，如果anchor template的iou大于阈值则归为正样本.

四、损失函数

损失分为三个部分：置信度损失，定位损失和类别损失.
$$L=L_{cls}+L_{conf}+L_{loc}$$
在正负样本匹配部分我已经解释过只有正样本才有这三类损失，而负样本只有置信度损失，所以在损失计算的过程中我们需要将anchor template划分为正样本与负样本两种情况来计算loss.

1.类别损失(只考虑正样本)

$Los{s}_{cls}$选用的是BCE损失函数：
$$L_{cls}=-\sum _{i\in pos}\sum _{j\in cls}(O_{ij}ln({\hat{C}}_{ij}))+(1-O_{ij})ln(1-{\hat{C}}_{ij})$$
$${\hat{C}}_{ij}=\sigma (C_{ij})$$
$O_{ij}$代表第i个正样本中的第j个类别是否存在，若存在则为1，不存在为0.(根据自己打的标签来)
${\hat{C}}_{ij}$代表经过sigmoid函数分类后的预测值.

上图是从原论文中截取的对分类损失函数的描述，作者的观点是获取好的分类性能并不一定要使用softmax，相反使用了使sigmoid函数分类和bce损失.
读到这儿，平时我们一般都使用softmax进行多分类，那为什么使用sigmoid进行分类？
independent logistic classifiers指的是sigmoid函数，个人的理解是：它的好处是将类别概率限制到[0,1]之间，且每个类别的概率值相互独立，互不影响，适用于多标签分类.softmax在进行分类时使所有类别概率总和为1，很多时候会出现“一家独大”的情况，即某一个类别占比较大，概率值较高，其他类别的概率值很低，在计算类别损失时无法达到一个好的效果，并不利于网络的收敛.
总而言之，softmax函数不适用于多标签分类，预测值通过sigmoid函数后每一类的值相互独立互不影响，适用于同时预测多类目标，即多标签分类.

2.置信度损失(考虑所有样本)

置信度$Los{s}_{conf}$计算公式如下所示：
$$Los{s}_{conf}=-\sum _i{O}_{i}ln({\hat{c}}_i)+(1-O_i)ln(1-{\hat{c}}_i)$$
$${\hat{C}}_i=\sigma (C_i)$$
$O_i$代表预测目标边界框i中是否真实存在目标.若存在则为1，不存在为0.(根据自己打的标签来)
${\hat{C}}_i$代表表示预测目标矩形框i内是否存在目标的Sigmoid概率.
Sigmoid函数作用主要是将预测值范围规定到[0,1]

yolov3论文中提出confidence score的预测使用的是一种逻辑回归的方式，所以损失函数用的是BCE.

3.定位损失(只考虑正样本)

置信度$Los{s}_{loc}$计算公式如下所示：
$$Los{s}_{loc}=\sum _{i\in pos}({\hat{t}}_{\ast }-t_{\ast }{)}^2$$

根据以上论文内容可知，计算$Los{s}_{loc}$时使用的时误差平方和公式，${\hat{t}}_{\ast }$为真实值，$t_{\ast }$为预测值
所以$Los{s}_{loc}$可写作如下形式
$$Los{s}_{loc(x,y)}=\sum _{i\in pos}\sum _{m\in x,y}[(g_m-c_m)-\sigma (t_m){]}^2$$
其中${\hat{t}}_{\ast }=g_m-c_m$，$t_{\ast }=\sigma (t_m)$
$$Los{s}_{loc(w,h)}=\sum _{i\in pos}\sum _{n\in w,h}(ln\frac{g_m^i}{p_n^i}-t_n{)}^2$$
其中${\hat{t}}_{\ast }=ln\frac{g_m^i}{p_n^i}$，$t_{\ast }=t_n$
$$Los{s}_{loc}=Los{s}_{loc(x,y)}+Los{s}_{loc(w,h)}$$
yolov3中的定位损失采用SSE显然是不太合适的，SSE主要是对预测所得anchor中心偏移量与宽高缩放因子进行误差分析，是对点进行回归分析，并不能较好的反应预测框与真实框之间的误差关系，这个问题我们将在下一节yolov4的讲解中进行讨论.