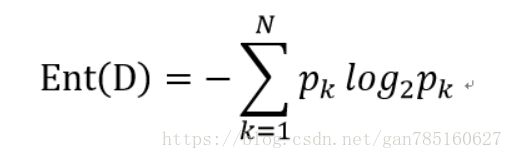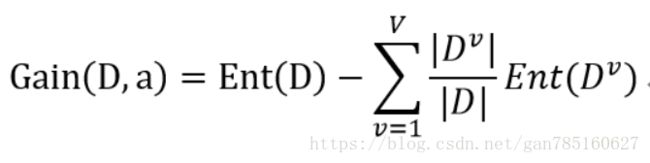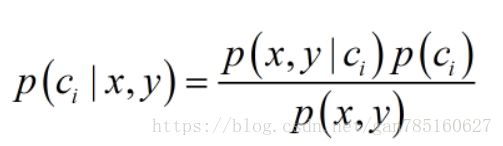机器学习方法简介（2）--决策树、随机森林、朴素贝叶斯
1.决策树
决策树是一种用于对实例进行分类的树形结构。
Hunt算法是一种采用局部最优策略的决策树构建算法，它同时也是许多决策树算法的基础，包括ID3、C4.5和CART等。
Hunt算法的递归定义如下：
(1) 如果 
中所有记录都属于同一个类，则 t 是叶结点，用 
标记。
(2) 如果 中包含属于多个类的记录，则选择一个属性测试条件（attribute test condition），将记录划分成较小的子集。对于测试条件的每个输出，创建一个子女结点，并根据测试结果将 中的记录分布到子女结点中。然后，对于每个子女结点，递归地调用该算法。
需要附加的条件来处理以下的情况：
- 算法的第二步所创建的子女结点可能为空，即不存在与这些结点相关联的记录。如果没有一个训练记录包含与这样的结点相关联的属性值组合，这种情形就可能发生。这时，该结点成为叶结点，类标号为其父结点上训练记录中的多数类。
- 在第二步，如果与相关联的所有记录都具有相同的属性值（目标属性除外），则不可能进一步划分这些记录。在这种情况下，该结点为叶结点，其标号为与该结点相关联的训练记录中的多数类。
在决策过程中，对于特征的选择还是比较重要的。随机选择显然是不好的，因此，我们定义了信息增益和信息增益比两个指标来指导特征选择。
信息熵的定义：
信息增益的定义：
信息增益率定义：
ID3算法应用了信息增益来选择特征 。
C4.5算法与上边的ID3算法非常相似，唯一的不同是，ID3算法是用信息增益来选择特征，而C4.5算法使用信息增益率来选择特征。在使用信息增益作为训练数据集特征时会偏向于取值较多的特征，而用信息增益率则避免了这一问题。
CART生成算法与C4.5算法相类似，它与C4.5算法的主要区别是使用基尼系数进行属性选择。
剪枝
作为决策树中一种防止Overfitting过拟合的手段，分为预剪枝和后剪枝两种。
预剪枝：当决策树在生成时当达到该指标时就停止生长，比如小于一定的信息获取量或是一定的深度，就停止生长。
后剪枝：当决策树生成完后，再进行剪枝操作。优点是克服了“视界局限”效应，但是计算量代价较大。
决策树优点：
直观，便于理解，在相对短的时间内能够对大型数据源做出可行且效果良好的结果，能够同时处理数据型和常规型属性。
决策树缺点：
可规模性一般，连续变量需要划分成离散变量，容易过拟合。
2.随机森林（RF）
随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。
随机森林中的每个决策树独立预测，然后对所有决策树的预测结果进行投票，将若干个弱分类器的分类结果进行投票选择，从而组成一个强分类器，这就是随机森林bagging的思想。
特点：
1）在当前所有算法中，具有极好的准确率。
2）能够有效地运行在大数据集上。
3）能够处理具有高维特征的输入样本，而且不需要降维。
4）能够评估各个特征在分类问题上的重要性。
5）在生成过程中，能够获取到内部生成误差的一种无偏估计。
6）对于缺省值问题也能够获得很好得结果。
每棵树的按照如下规则生成：
1）如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本（这种采样方式称为bootstrap sample方法），作为该树的训练集；
2）如果每个样本的特征维度为M，指定一个常数m<
3）每棵树都尽最大程度的生长，并且没有剪枝过程。
随机森林分类效果（错误率）与两个因素有关：
- 森林中任意两棵树的相关性：相关性越大，错误率越大；
- 森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低。
减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键问题是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数。
3.朴素贝叶斯
基于概率论的分类算法，通过考虑特征概率来预测分类。
贝叶斯法则
假如我们有c0和c1两个类，给定一个数据，它的特征为x1,x2,x3，我们求这个数据属于哪个类。
首先我们需要求p（c0|x1,x2,x3）和p（c1|x1,x2,x3）哪个更大，如果p（c0|x1,x2,x3）更大，则该数据属于c0类，反之属于c1类。
但是p（c0|x1,x2,x3）不好求解，所以我们利用贝叶斯法则将其转化为求解陪p（x1,x2,x3|c0）、p（c0）、p（x1,x2,x3）的问题。
引用《决策树简述》
引用《数据挖掘十大算法之决策树详解（1）》
引用《决策树 (Decision Tree) 原理简述及相关算法(ID3,C4.5)》
引用《随机森林（Random Forest）》
引用《带你搞懂朴素贝叶斯分类算法》