轻量化网络ShuffleNet MobileNet v1/v2/v3( MobileNet)学习笔记
轻量化网络ShuffleNet MobileNet v1/v2学习笔记
部分取自(giantpandacv公众号)
在学习这两部分之前,大家应该要懂一个卷积操作,分组卷积和深度可分离卷机。其实他们的原理差不多,我在这里就不详细讲了,不清楚的同学可以查看我的这篇博文这篇博文几乎涵盖了现在神经网络中大部分的卷积的骚操作,看完以后相信你就会茅塞顿开的。
MobileNet v1
文章链接
Mobilenet v1是Google于2017年发布的网络架构,旨在充分利用移动设备和嵌入式应用的有限的资源,有效地最大化模型的准确性,以满足有限资源下的各种应用案例。Mobilenet v1也可以像其他流行模型(如VGG,ResNet)一样用于分类、检测、嵌入和分割等任务提取图像卷积特征。
Mobilenet v1核心是把卷积拆分为Depthwise+Pointwise两部分。
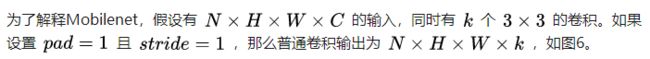
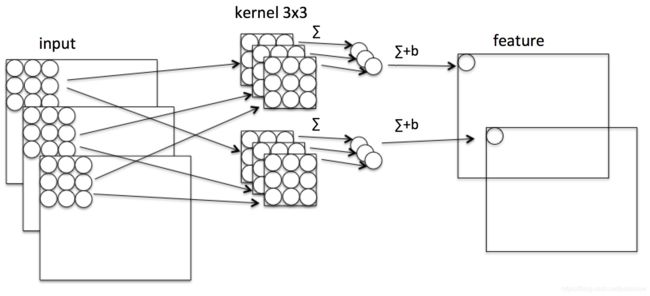

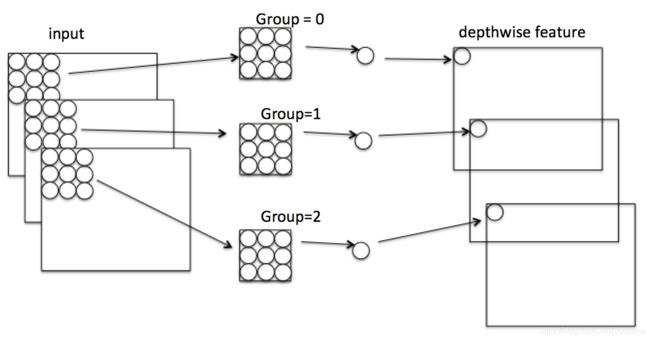

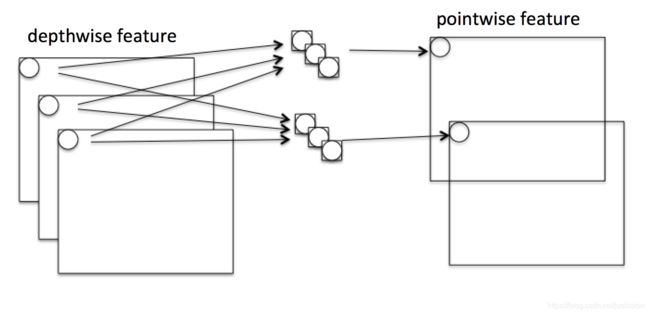
这样就把一个普通卷积拆分成了Depthwise+Pointwise两部分。其实Mobilenet v1就是做了如下转换:
普通卷积:3x3 Conv+BN+ReLU
Mobilenet卷积:3x3 Depthwise Conv+BN+ReLU 和 1x1 Pointwise Conv+BN+ReLU
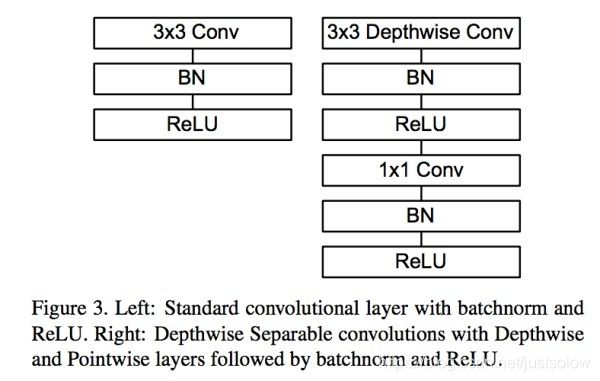
通过Depthwise+Pointwise的拆分,相当于将普通卷积的计算量压缩为:
depthwise + pointwise conv = H × W × C × 3 × 3 + H × W × C × k H × W × C × 3 × 3 = 1 k + 1 3 × 3 \frac{\text {depthwise + pointwise}}{\text {conv}}=\frac{H \times W \times C \times 3 \times 3+H \times W \times C \times k}{H \times W \times C \times 3 \times 3}=\frac{1}{k}+\frac{1}{3 \times 3} convdepthwise + pointwise=H×W×C×3×3H×W×C×3×3+H×W×C×k=k1+3×31
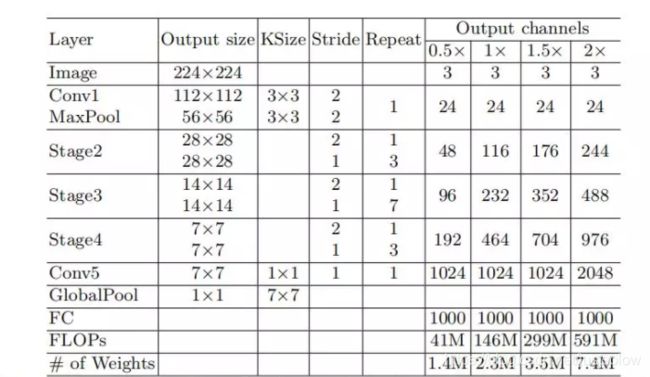
Mobilenet v1还给出了基本网络结构
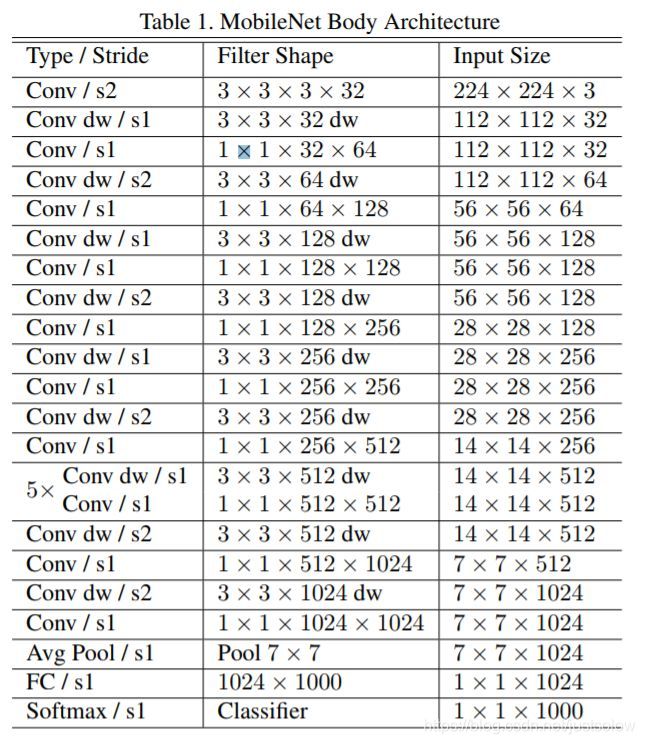
在此基础上,MobileNet v1还进行了两个优化:
宽度乘法器:更薄的模型
宽度乘法器α的作用就是对每一层均匀薄化。给定一个层以及宽度乘法器α,输入通道数M变成了αM并且输出通道数变成αN。
加上宽度乘法器的深度可分离卷积的计算量如下:DK∗DK∗αM∗DF∗DF+αM∗αN∗DF∗DF
由于α∈(0,1],一般设置为1\0.75\0.5\0.25。当α=1的时候就是最基本的MobileNet,当α<1时,就是薄化的MobileNet。宽度乘法器对计算量和参数量的减少大约α2倍。宽度乘法器可以应用在任何模型结构来定义一个更瘦的模型,并且权衡合理的精度、延迟的大小。宽度乘法器常用来薄化一个新的需要从头开始训练的网络结构。
分辨率乘法器:约化表达
第二个薄化神经网络计算量的超参数是分辨率乘法器ρ。我们将其应用在输入图片以及每一层的内部表达中。实际上,我们通过设置ρ来隐式的设置输入的分辨率大小。
我们现在可以对网络中的核心层的深度可分离卷积加上宽度乘法器α以及分辨率乘法器ρ来表达计算量:DK∗DK∗αM∗ρDF∗ρDF+αM∗αN∗ρDF∗ρDF
其中ρ∈(0,1],一般隐式的设置以便于输入网络的图像分辨率为224\192\160\128等。当ρ=1时为最基本的MobileNet,当ρ<1时,则为薄化的MobileNet。分辨率乘法器对网络约化大约ρ2倍。

MobileNet v2
文章链接
MobileNet V2是Google继V1之后提出的下一代轻量化网络,主要解决了V1在训练过程中非常容易特征退化的问题,V2相比V1效果有一定提升。
经过VGG,Mobilenet V1,ResNet等一系列网络结构的提出,卷积的计算方式也逐渐进化。
但是作者在文章中提出了几个问题。而MobileNet v2就是解决了MobileNet v1的这几个问题。
问题1:ReLU造成的低维度数据坍塌(collapses)
channel少的feature map不应后接ReLU,否则会破坏feature map。

问题2:没有复用特征
在神经网络训练中如果某个卷积节点权重的值变为0就会“死掉”。因为对于任意输入,该节点的输出都是0。而ReLU对0值的梯度是0,所以后续无论怎么迭代这个节点的值都不会恢复了。而通过ResNet结构的特征复用,可以很大程度上缓解这种特征退化问题,如图18(这也从一个侧面说明ResNet为何好于VGG)。另外,一般情况训练网络使用的是float32浮点数;当使用低精度的float16时,这种特征复用可以更加有效的减缓退化。
基于上述两个问题,Mobilenet v2提出了Linear Bottlenecks+Inverted residual block作为网络基本结构,如图19。
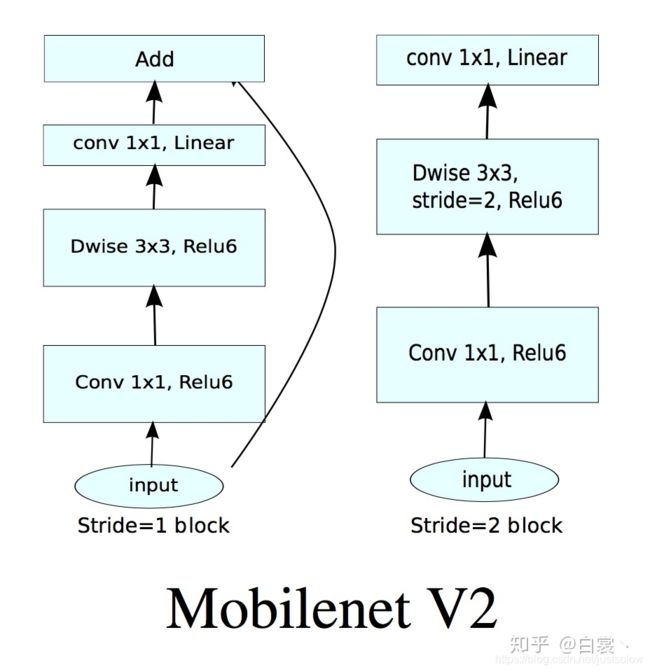
理解之前的问题后看,其实Mobilenet V2使用的基本卷积单元结构有以下特点:
整体上继续使用Mobilenet V1的Separable convolution降低卷积运算量。
引入了特征复用结构。
采用Inverted residual block结构。该结构使用Point wise convolution先对feature map进行升维,再在升维后的特征接ReLU,减少ReLU对特征的破坏。
下面是residual block结构和Inverted residual block结构:
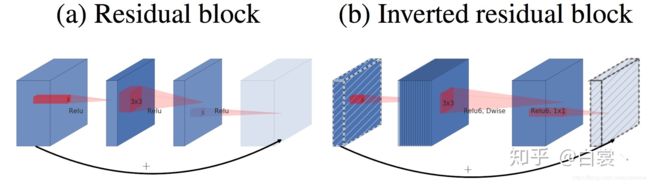
上图左边(a)图的传统的residual block,先用1x1卷积将输入的feature map的维度降低,然后进行3x3的卷积操作,最后再用1x1的卷积将维度变大。右边(b)图即为本文提出的结构,先用1x1卷积将输入的feature map维度变大,然后用3x3 depthwise convolution方式做卷积运算,最后使用1x1的卷积运算将其维度缩小。注意,此时的1x1卷积运算后,不再使用ReLU激活函数,而是使用线性激活函数,以保留更多特征信息,保证模型的表达能力。
该block具体结构如下:
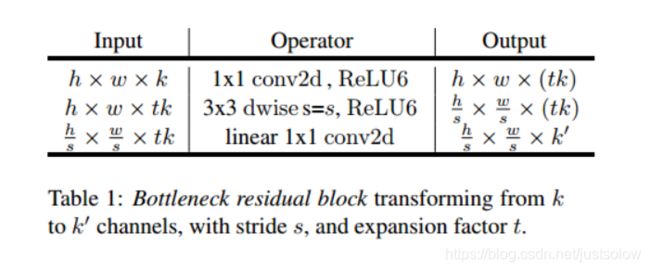
最后总结一下两者的区别:
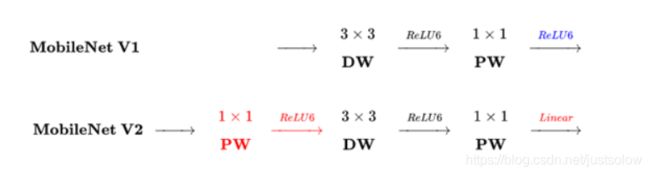
主要区别有两点:
(1)Depth-wise convolution之前多了一个1*1的“扩张”层,目的是为了提升通道数,获得更多特征;
(2)最后不采用Relu,而是Linear,目的是防止Relu破坏特征。
MobileNet V3
论文原文:https://arxiv.org/pdf/1905.02244.pdf
源码实现:https://github.com/xiaolai-sqlai/mobilenetv3
MobileNetV3是Google继MobileNet V1和MobileNet V2后的新作,主要使用了网络搜索算法(用NAS通过优化每个网络块来搜索全局网络结构,用NetAdapt算法搜索每个层的滤波器数量),同时在MobileNet V2网络结构基础上进行改进,并引入了SE模块和提出了H-Swish激活函数。
- 引入SE模块
下面的Figure3表示了MobileNet V2 Bottleneck的原始网络结构,然后Figure4表示在MobileNet V2 Bottleneck的基础上添加了一个SE模块。因为SE结构会消耗一定的时间,SE瓶颈的大小与卷积瓶颈的大小有关,我们将它们全部替换为固定为膨胀层通道数的1/4。这样做可以在适当增加参数数量的情况下提高精度,并且没有明显的延迟成本。并且SE模块被放在了Depthwise卷积后面。

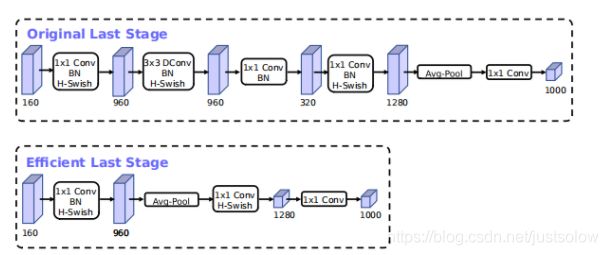
2. 更改网络末端计算量大的层
MobileNetV2的inverted bottleneck结构是使用了11卷积作为最后一层,以扩展到高维度的特征空间(也就是下图中的320->1280那一层的11卷积)。这一层的计算量是比较大的。MobileNetV3为了减少延迟并保留高维特性,将该11层移到最终的平均池化之后(960->Avg Pool->11 Conv)。现在计算的最后一组特征图从77变成了11,可以大幅度减少计算量。最后再去掉了Inverted Bottleneck中的Depthwise和1*1降维的层,在保证精度的情况下大概降低了15%的运行时间。
3. 更改初始卷积核的个数
修改网络头部卷积核通道数的数量,Mobilenet v2中使用的是,作者发现,其实32可以再降低一点,所以这里改成了16,在保证了精度的前提下,降低了3ms的速度。
4. H-Swish 激活函数
Mobilenet V3引入了新的非线性激活函数:H-Wwish。它是最近的Swish非线性函数的改进版本,计算速度比Swish更快(但比ReLU慢),更易于量化,精度上没有差异。其中Swish激活函数的公式如下:
swish ( x ) = x ∗ δ ( x ) \operatorname{swish}(x)=x * \delta(x) swish(x)=x∗δ(x)
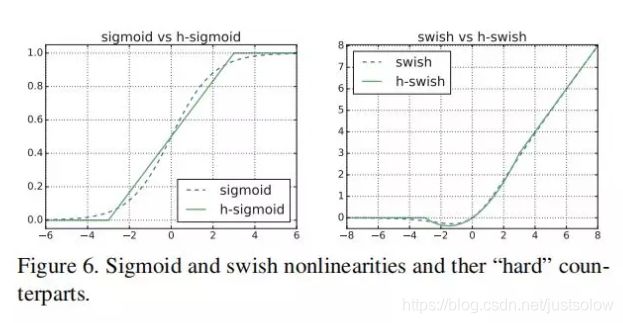
其中 δ ( x ) \delta(x) δ(x)是sigmoid激活函数,而H-Swish的公式如下:
h − swish ( x ) = x ReLU ( x + 3 ) 6 h-\operatorname{swish}(x)=x \frac{\operatorname{ReLU}(x+3)}{6} h−swish(x)=x6ReLU(x+3)
简单说下,Swish激活函数相对于ReLU来说提高了精度,但因为Sigmoid函数而计算量较大。而H-swish函数将Sigmoid函数替换为分段线性函数,使用的ReLU6在众多深度学习框架都可以实现,同时在量化时降低了数值的精度损失。下面这张图提到使用H-Swish在量化的时候可以提升15%的精度,还是比较吸引人的。
5. NAS搜索全局结构和NetAdapt搜索层结构
比较复杂,不太清楚。感兴趣的可以去查看原文和源码。
网络结构一种small一种large
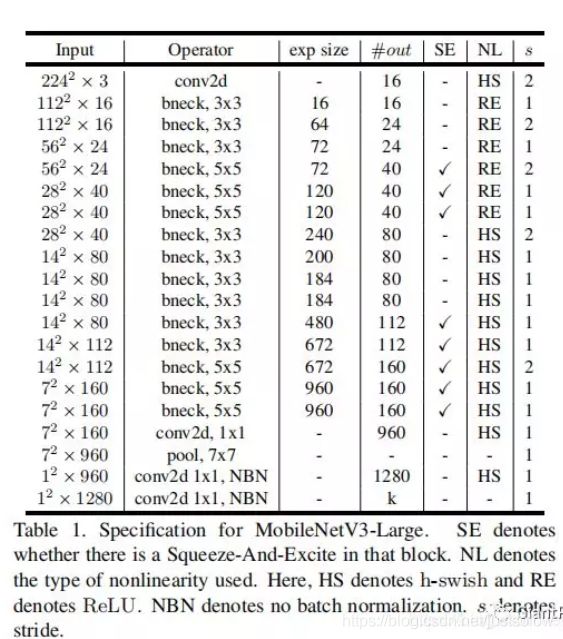
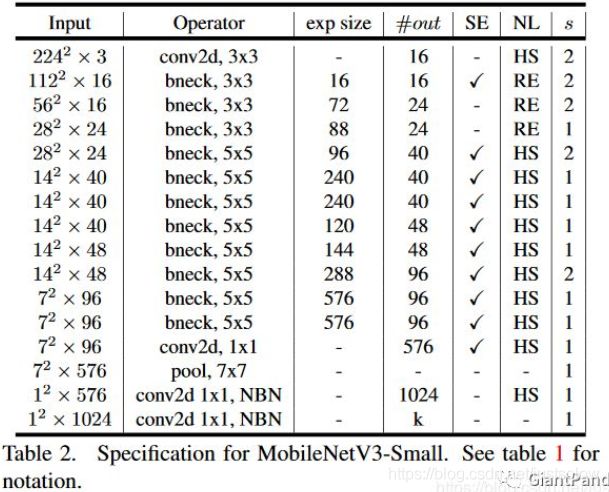
small结构可视图:

ShuffleNet V1
文章链接
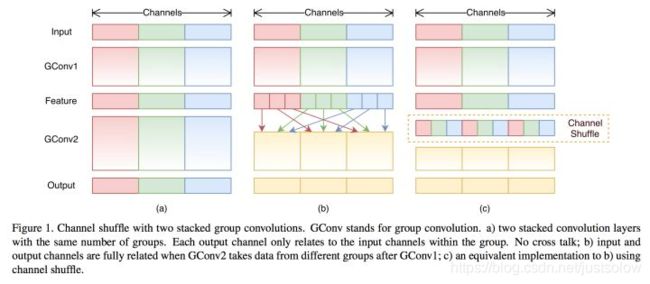
ShuffleNet是Face++提出的一种轻量化网络结构,主要思路是使用Group convolution和Channel shuffle改进ResNet,可以看作是ResNet的压缩版本。
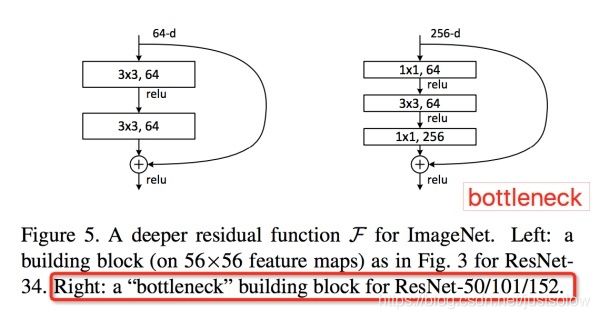
这是resnet的两种经典的结构:注意Channel维度变化: 256 D → 64 D → 256 D 256 D \rightarrow 64 D \rightarrow 256 D 256D→64D→256D,宛如一个中间细两端粗的瓶颈,所以称为“bottleneck”。这种结构相比VGG,早已经被证明是非常效的,能够更好的提取图像特征。
下图展示了ShuffleNet的结构,其中(a)就是加入Depthwise的ResNet bottleneck结构,而(b)和©是加入Group convolution和Channel Shuffle的ShuffleNet的结构。
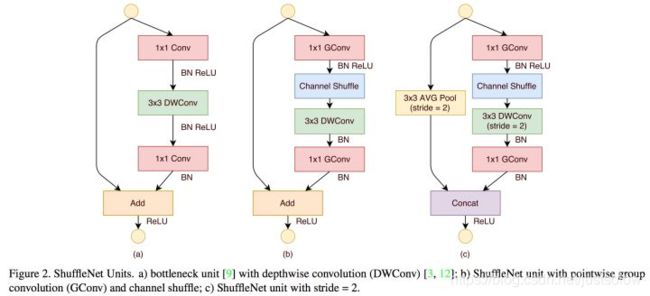
计算一下计算量:

计算细节如下,对于图14 (a):
输入是H×W×C,第一个卷积是1×1×k,输出为H×W×k,计算量为H×W×C×k;
输入到Depthwise,卷积为3×3×k,输出为H×W×k,计算量为H×W×3×3×k;
输入到1×1Conv,卷积核为1×1×C,输出为H×W×C,计算量为H×W×k×C;
最终计算量相加为:HW(2Ck+9k);
对于图14(b),与上面不同的是把Conv1×1换成GConv1×1,相当于计算量从H×W×C×k变为H×W×C×k/g,同时还引入了shuffle cost。
相比原始加入Depthwise的ResNet缩小了很多的计算量。所以ShuffleNet相当于保留ResNet结构,同时又压低计算量的改进版。
这里解释下为何要做Channel Shuffle操作:
ShuffleNet的本质是将卷积运算限制在每个Group内,这样模型的计算量取得了显著的下降。然而导致模型的信息流限制在各个Group内,组与组之间没有信息交换,如图15,这会影响模型的表示能力。因此,需要引入组间信息交换的机制,即Channel Shuffle操作。同时Channel Shuffle是可导的,可以实现end-to-end一次性训练网络。
1、Shuffle channel在实现的时候需要大量的指针跳转和Memory set,这本身就是极其耗时的;同时又特别依赖实现细节,导致实际运行速度不会那么理想。
2、Shuffle channel规则是人工设计出来的,不是网络自己学出来的。这不符合网络通过负反馈自动学习特征的基本原则,又陷入人工设计特征的老路(如sift/HOG等)。
ShuffleNet V2
论文原文:https://arxiv.org/pdf/1807.11164.pdf
代码实现:https://github.com/anlongstory/ShuffleNet_V2-caffe
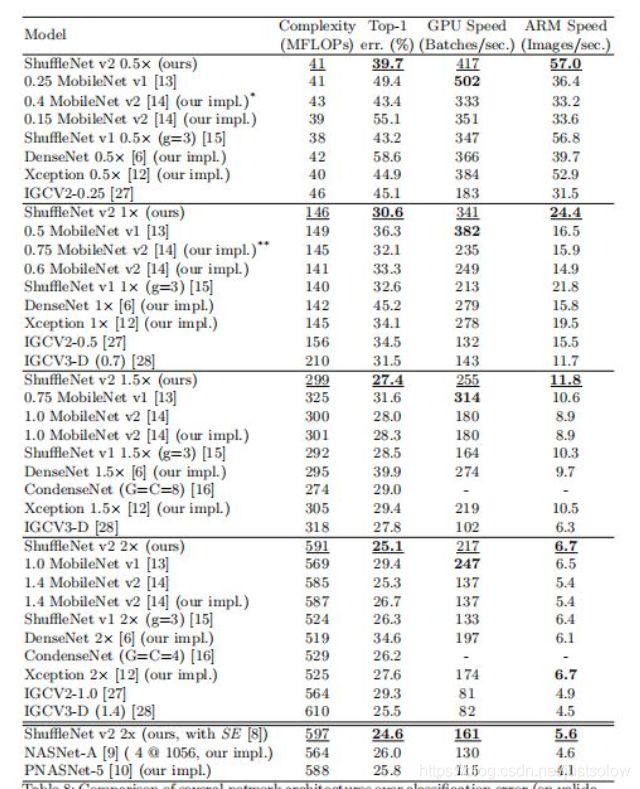
那么ShuffleNet V2是解决了V1的那些问题呢?
作者做了四个实验:
1、探索卷积层的输入输出特征通道数对MAC指标的影响。
实验结论是卷积层的输入和输出特征数相等时MAC最小,此时模型的速度最快。
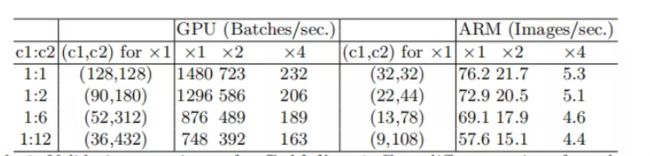
2、探索卷积的group操作对MAC的影响。
实验结论是过多的group操作会增大MAC,从而使模型变慢。

3、探索模型设计的分支数量对模型速度的影响。
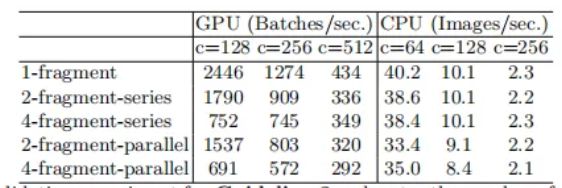
实验结论是模型中的分支数量越少,模型速度越快。
其中2-fragment-series表示一个block中有2个卷积层串行,也就是简单的堆叠。而2-fragment-parallel表示一个block中有2个卷积层并行,类似于Inception的整体设计。可以看出在相同FLOPS的情况下,单卷积层(1-fragment)的速度最快。因此模型支路越多(fragment程度越高)对于并行计算越不利,导致模型变慢,在GPU上这个影响更大,在ARM上影响相对小一点。
4、探索element-wise操作对模型速度的影响。
实验结论是element-wise操作所带来的时间消耗远比在FLOPS上体现的数值要多,因此要尽可能减少element-wise操作。
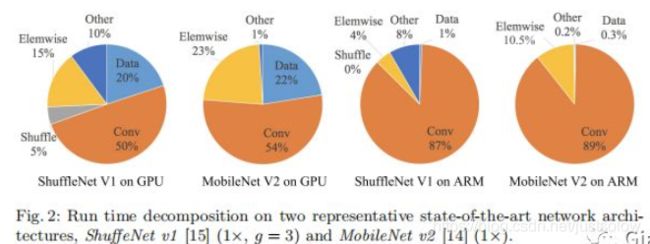
可以看到FLOPS主要表示的是卷积层的时间消耗,而ElementWise操作虽然基本不增加FLOPS,但是带来的时间消耗占比却不可忽视。
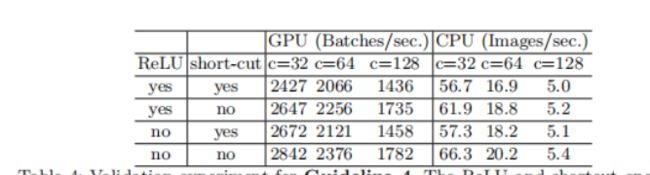
因此论文做了实验4,实验4是运行了10次ResNet的bottleneck来计算的,short-cut表示的就是element-wise操作。同时作者这里也将depthwise convolution归为element-wise操作,因为depthwise-wise convolution也具有低FLOPS,高MAC的特点。实验结果如Table4所示。
ShuffleNet V2 瓶颈结构设计
如Figure3所示。这张图中的(a)和(b)是ShuffleNet V1的两种不同的block结构,两者的差别在于(b)对特征图分辨率做了缩小。©和(d)是ShuffleNet V2的两种不同结构。从(a)和©对比可知©在开头增加了一个通道分离(channel split)操作,这个操作将输入特征通道数c分成了 c − c ′ c-c^{\prime} c−c′和 c ′ c^{\prime} c′,在论文中 c ′ c^{\prime} c′取 c ′ / 2 c^{\prime}/2 c′/2,这主要是为了改善实验1。然后©取消了1x1卷积层中的分组操作,这主要为了改善实验2的结论,同时前面的通道分离其实已经算是变相的分组操作了。其次,channel shuffle操作移动到了concat操作之后,这主要为了改善实验3的结果,同时也是因为第一个1x1卷积层没有分组操作,所以在其后面跟channel shuffle也没有太大必要。最后是将element-wise add操作替换成concat,这和前面的实验4的结果对应。(b)和(d)的对比也是同理,只不过因为(d)的开始处没有通道分离操作,所以最后concat后特征图通道数翻倍。
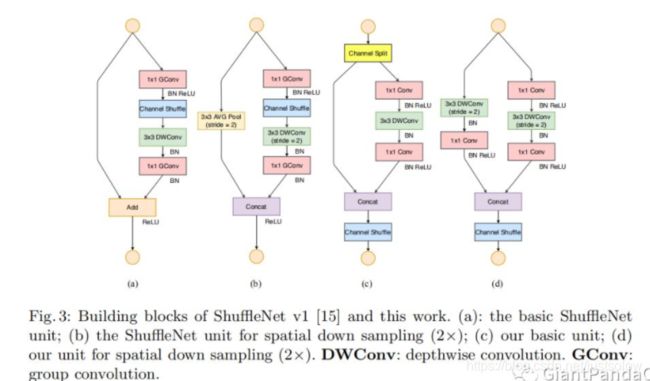
上图(a) ShuffleNet v1 ,(b)ShuffleNet v1 降采样, ©ShuffleNet v2,(d)ShuffleNet v2 降采样
1、在©中ShuffleNet v2使用了一个通道分割(Channel Split)操作。这个操作非常简单,即将 c 个输入Feature分成 c-c’ 和 c’ 两组,一般情况下 c’ = c/2 。
2、分割之后的两个分支。为了满足G3, 左侧是一个恒等映射,通道数量保持不变(我感觉也满足G1)。右侧是一个输入通道数和输出通道数均相同的卷积,满足G1。
3、在右侧的卷积中, 1x1 卷积并没有使用分组卷积,这部分是为了遵循 G2,部分是因为分割操作已经产生了两个组。
4、最后在合并的时候均是使用拼接(Concat)操作,拼接后整个模块的通道数量保持不变,是为了满足G1。使用concat 代替原来的 elementy-wise add,并且后面不加 ReLU,满足G4。
拼接后接一个和ShuffleNet v1中一样的Channel Shuffle操作。在堆叠ShuffleNet v2的时候,通道拼接、通道洗牌和通道分割可以合并成1个element-wise操作,也是为了满足G4。