机器学习算法- 数据分析、数据挖掘

数学基础

---

0. 矩阵求导（需要了解矩阵定义，偏导求法）

机器学习中的矩阵向量求导(一) 求导定义与求导布局 - 刘建平Pinard - 博客园

分子分母布局：求导先以分子还是分母展开

矩阵的迹（方阵）：主对角线元素之和

聚类分析

---

0. 简介

聚类分析又叫群分析，是对多个样本（或指标）进行定量分类的一种多元统计分析方法。对样本进行分类称为Q型聚类分析，对指标进行分类称为R型聚类分析。

1. 算法

• K-means聚类、K-中心点聚类、CLARANS算法(基于随机选择), DIANA算法(自顶向下层次聚类算法)、BIRCH算法、Chameleon算法
• EM算法 （最大期望算法）
• OPTICS算法、DBSCAN算法 （基于密度）

2. 聚类原理

2.1. 相似性衡量（similarity measurement）

（1）距离。距离主要就是指Minkovski距离。这个名字虽然听起来陌生，但其算法就是Lp norm的算法：

如果是L1 norm，那就是绝对值/曼哈顿距离（Manhattan distance）；

如果是L2 norm，那就是著名的欧式距离（Euclidean distance）了，也是应用最广泛的；

（2）相似系数。主要有夹角余弦和相关系数。相关系数的应用也非常广泛，其主要优势是它不受原线性变换的影响，而且可以轻松地转换为距离，但其运算速度要比距离法慢得多，当维数很高的时候。

（3）核函数K(x,y)。核函数的功能就是把数据从低维空间投影（project）到高维空间，使得线性可分。

（4）DTW（dynamic time warping）。它是一种非常特殊的距离算法，它可以计算两个不同长度的向量的距离，也可以对两对向量中不同时间段内的数据做匹配，比如你发现2015年上半年的上证指数走势和SP5002012年的走势非常相似。DTW主要用在时间序列的部分场合里。

2.2. 聚类算法（clustering algorithm）

（1）Hierarchical methods（分层方法）：该主要有两种路径：agglomerative和divisive，也可以理解为自下而上法（bottom-up）和自上而下法（top-down）。

自下而上法就是一开始每个个体（object）都是一个类，然后根据linkage寻找同类，最后形成一个“类”。

自上而下法就是反过来，一开始所有个体都属于一个“类”，然后根据linkage排除异己，最后每个个体都成为一个“类”。

至于根据Linkage判断“类”的方法就是楼上所提到的最短距离法、最长距离法、中间距离法、类平均法等等（其中类平均法往往被认为是最常用也最好用的方法，一方面因为其良好的单调性，另一方面因为其空间扩张/浓缩的程度适中）。

• BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies，使用层次结构的平衡迭代约简和聚类）主要是在数据体量很大的时候使用，而且数据类型是numerical；
• ROCK（A Hierarchical Clustering Algorithm for Categorical Attributes，一种分类属性的分层聚类算法）主要用在categorical的数据类型上；
• Chameleon（A Hierarchical Clustering Algorithm Using Dynamic Modeling，一种基于动态建模的分层聚类算法）里用到的linkage是kNN（k-nearest-neighbor）算法，并以此构建一个graph，Chameleon的聚类效果被认为非常强大，比BIRCH好用，但运算复杂的发很高，O(n^2)。

（2）Partition-based methods（基于分区的方法）：其原理简单来说就是，想象你有一堆散点需要聚类，想要的聚类效果就是“类内的点都足够近，类间的点都足够远”。

首先你要确定这堆散点最后聚成几类，然后挑选几个点作为初始中心点，再然后依据预先定好的启发式算法（heuristic algorithms）给数据点做迭代重置（iterative relocation），直到最后到达“类内的点都足够近，类间的点都足够远”的目标效果。

也正是根据所谓的“启发式算法”，形成了k-means算法及其变体包括k-medoids、k-modes、k-medians、kernel k-means等算法。

• k-means对初始值的设置很敏感，所以有了k-means++、intelligent k-means、genetic k-means；
• k-means对噪声和离群值非常敏感，所以有了k-medoids和k-medians；
• k-means只用于numerical类型数据，不适用于categorical类型数据，所以k-modes；
• k-means不能解决非凸（non-convex）数据，所以有了kernel k-means。

另外，很多教程都告诉我们Partition-based methods聚类多适用于中等体量的数据集，但我们也不知道“中等”到底有多“中”，所以不妨理解成，数据集越大，越有可能陷入局部最小。下图显示的就是面对非凸，k-means和kernel k-means的不同效果。

（3）Density-based methods（基于密度的方法）：上面这张图你也看到了，k-means解决不了这种不规则形状的聚类。于是就有了Density-based methods来系统解决这个问题。该方法同时也对噪声数据的处理比较好。其原理简单说画圈儿，其中要定义两个参数，一个是圈儿的最大半径，一个是一个圈儿里最少应容纳几个点。最后在一个圈里的，就是一个类。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）就是其中的典型，可惜参数设置也是个问题，对这两个参数的设置非常敏感。

DBSCAN的扩展叫OPTICS（Ordering Points To Identify Clustering Structure）通过优先对高密度（high density）进行搜索，然后根据高密度的特点设置参数，改善了DBSCAN的不足。下图就是表现了DBSCAN对参数设置的敏感，你们可以感受下。

 （4）Grid-based methods（基于网格的方法）：这类方法的原理就是将数据空间划分为网格单元，将数据对象集映射到网格单元中，并计算每个单元的密度。根据预设的阈值判断每个网格单元是否为高密度单元，由邻近的稠密单元组形成”类“。该类方法的优点就是执行效率高，因为其速度与数据对象的个数无关，而只依赖于数据空间中每个维上单元的个数。但缺点也是不少，比如对参数敏感、而只依赖于数据空间中每个维上单元的个数。CLIQUE（CLustering In QUEst）是该类方法中的代表性算法。下图是CLIQUE的一个例子：

（5）Model-based methods（基于模型的方法）：这一类方法主要是指基于概率模型的方法和基于神经网络模型的方法，尤其以基于概率模型的方法居多。 

这里的概率模型主要指概率生成模型（generative Model），同一”类“的数据属于同一种概率分布。这中方法的优点就是对”类“的划分不那么”坚硬“，而是以概率形式表现，每一类的特征也可以用参数来表达；但缺点就是执行效率不高，特别是分布数量很多并且数据量很少的时候。其中最典型、也最常用的方法就是高斯混合模型（GMM，Gaussian Mixture Models）。

基于神经网络模型的方法主要就是指SOM（Self Organized Maps）了，也是我所知的唯一一个非监督学习的神经网络了。下图表现的就是GMM的一个demo，里面用到EM算法来做最大似然估计。

2.3. 数据简化（data reduction）

这个环节optional。其实第二部分提到的有些算法就是对数据做了简化，才得以具备处理大规模数据的能力，比如BIRCH。但其实你可以任意组合，所以理论上把数据简化的方法和上面提到的十几种聚类算法结合使用，可以有上百个算法了。

（1）变换（Data Transformation）：离散傅里叶变换（Discrete Fourier Transformation）可以提取数据的频域（frequency domain）信息，离散小波变换（Discrete Wavelet Transformation）除了频域之外，还可以提取到时域（temporal domain）信息。

（2）降维（Dimensionality Reduction）：在降维的方法中，PCA（Principle Component Analysis）和SVD（Singular Value Decomposition）作为线性方法，受到最广泛的应用。还有像MDS（Multi-Dimensional Scaling）什么的，不过只是作为PCA的一个扩展，给我的感觉是中看不中用。这几个方法局限肯定是无法处理非线性特征明显的数据。处理非线性降维的算法主要是流形学习（Manifold Learning），这又是一大块内容，里面集中常见的算法包括ISOMAP、LLE（Locally Linear Embedding）、MVU（Maximum variance unfolding）、Laplacian eigenmaps、Hessian eigenmaps、Kernel PCA、Probabilistic PCA等等。流形学习还是挺有趣的，而且一直在发展。关于降维在聚类中的应用，最著名的应该就是谱聚类（Spectral Clustering），就是先用Laplacian eigenmaps对数据降维（简单地说，就是先将数据转换成邻接矩阵或相似性矩阵，再转换成Laplacian矩阵，再对Laplacian矩阵进行特征分解，把最小的K个特征向量排列在一起），然后再使用k-means完成聚类。谱聚类是个很好的方法，效果通常比k-means好，计算复杂度还低，这都要归功于降维的作用。

（3）抽样（Sampling）：最常用的就是随机抽样（Random Sampling）咯，如果你的数据集特别大，随机抽样就越能显示出它的低复杂性所带来的好处。比如CLARA（Clustering LARge Applications）就是因为k-medoids应对不了大规模的数据集，所以采用sampling的方法。至于更加fancy的抽样方法我还真不了解，我就不在这里好为人师而误人子弟了。

关联规则分析

---

1. 关联三度（支持度，置信度，提升度）

 2. Apriori算法

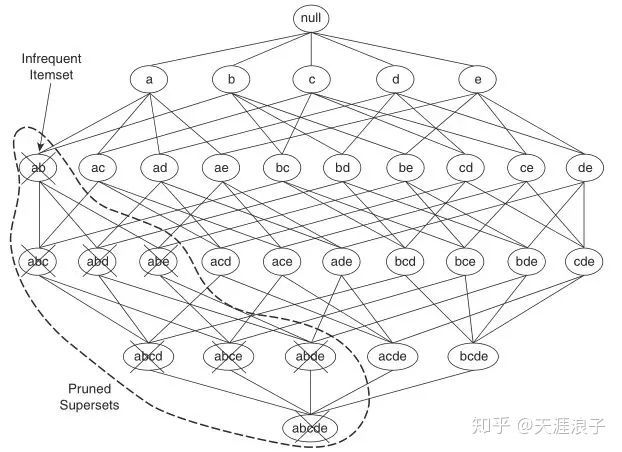
2.1 生成频繁项集 （候选项集）

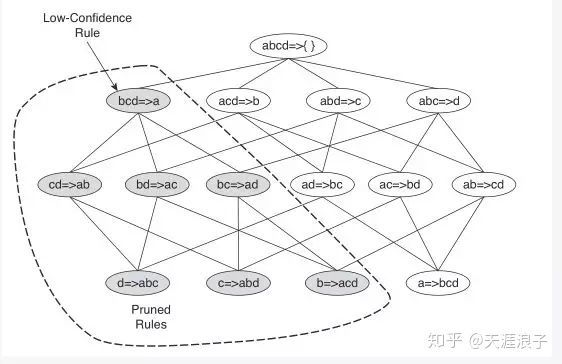
2.2 关联规则生成

3. FP-growth算法

机器学习算法

---

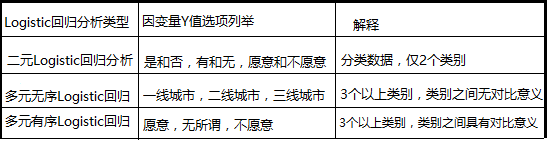
逻辑回归Logistic Regression

Logistic回归和线性回归最大的区别在于，Y的数据类型。线性回归分析的因变量Y属于定量数据，而Logistic回归分析的因变量Y属于分类数据

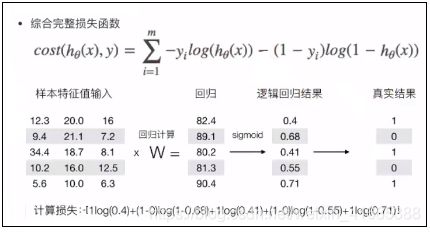
原理

聚类算法

1. 基于分层的方法

from scipy.cluster.hierarchy import linkage, fcluster, dendrogram

层次聚类会输出一个linkage矩阵Z，这个矩阵由四列组成，第一列和第二列分别是聚类簇的编号，在初始距离前每个初始值被从0到n-1进行标识，每生成一个聚类簇就在此基础上增加一对新的聚类簇；第三列表示前面两个聚类簇之间的距离；第四列表示新生成的聚类簇包含的元素的个数。

Z = linkage(sample, metric='euclidean', method='single')

#使用fcluster输出每个元素的所属类别
data['cluster'] = fcluster(Z, 4, criterion='maxclust')

method 是指计算类间距离的方法,比较常用的有3种:
(1)single:最近邻,把类与类间距离最近的作为类间距
(2)average:平均距离,类与类间所有pairs距离的平均
(3)complete:最远邻,把类与类间距离最远的作为类间距

2. 基于分区的方法Kmeans

k-means模型的一种理解思路是，它在每个类蔟的中心放置了一个圈（或者，更高维度超球面)，其半径由聚类中最远的点确定。该半径充当训练集中聚类分配的一个硬截断：任何圈外的数据点不被视为该类的成员。这些聚类模式必须是圆形的。k-means没有内置的方法来计算椭圆形或椭圆形的簇。 

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters= 7, init="random", n_init=1, max_iter=12).fit(data_kmeans)
data_kmeans["cluster"] = kmeans.labels_

k-means的两大缺陷 -- 聚类形状的不够灵活和缺少聚类分配的概率值，意味着许多数据集(尤其是低维数据集)，可能不会有预期的效果。GMM可以解决这些问题。

 

3. 基于密度的聚类分析DBSCAN

from sklearn.cluster import DBSCAN
DBSCAN(eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30, p=None, n_jobs=1)

cluster = DBSCAN(eps=0.5, min_samples=6).fit(data_dbs)
data_dbs["cluster"] = cluster.labels_

 基于密度的聚类有以下优点：

1. 能克服基于划分（距离）的算法只能发现类圆形（凸）的聚类的缺点
2. 可以发现任意形状的聚类，且对噪声数据不敏感
3. 不需要指定类的数目n_clusters
4. 算法中只有两个参数，即扫描半径eps和最小包含点数min_samples

缺点：

1. 计算复杂度较高
2. 受eps影响较大。在类中的数据分布不均匀时，eps较小时，密度小的cluster会被划分成多个性质类似的cluster；当eps较大时，会使得距离较近且密度较大的cluster被合并成一个cluster

 

4. 基于概率模型：高斯混合模型GMM（Gaussian Mixture Model）

使用了高斯分布作为参数模型，并使用了期望最大（Expectation Maximization，简称EM）算法进行训练。特定约束条件下，K-means算法可以被看作是高斯混合模型（GMM）的一种特殊形式。

高斯混合模型是对高斯模型进行简单的扩展，GMM使用多个高斯分布的组合来刻画数据分布。

这个公式的分布概率是K个高斯分布的和，每个高斯分布有属于自己的μ和σ参数，以及对应的权重参数，权重值必须为正数，所有权重的和必须等于1，以确保公式给出数值是合理的概率密度值。换句话说如果我们把该公式对应的输入空间合并起来，结果将等于1。 

高斯不仅局限于一维，很容易将均值扩展为向量，标准差扩展为协方差矩阵，用n-维高斯分布来描述多维特征。

从本质上说，高斯混合模型与k-means非常相似：它使用期望-最大化（EM算法）的方式，定性地执行以下操作：

1. 选择位置和形状的初始猜想
2. 重复直到收敛
   1. E步骤：对于每个点，计算其属于每个类别的概率权重
   2. M步骤：对于每个类别，使用E步算出的权重，根据所有数据点，更新其位置，规范化和形状

结果是，每个类别不是被硬边界的球体界定，而是平滑的高斯模型。正如在k-means的期望-最大方法一样，这种算法有时可能会错过全局最优解，因此在实践中使用多个随机初始化。

 设置不同的协方差类型控制每个类簇的形状的自由度：

 

from sklearn.mixture import GaussianMixture as GMM


'''选择合适的参数'''
n_components = np.arange(1, 21)
models = [GMM(n, covariance_type='full', random_state=0).fit(Xmoon)
          for n in n_components]

#aic(X) Akaike 信息标准
#bic(X) 贝叶斯信息准则
plt.plot(n_components, [m.bic(Xmoon) for m in models], label='BIC') 
plt.plot(n_components, [m.aic(Xmoon) for m in models], label='AIC') 
plt.legend(loc='best')
plt.xlabel('n_components');


print(gmm.converged_)   #判断是否收敛

gmm = GMM(n_components=2, covariance_type='full', random_state=0)
gmm.fit(Xmoon)
gmm.predict(Xmoon)  #预测分类
gmm.sample(1000)  #生成类似分布的数据

1. n_components: 混合高斯模型个数，默认为 1 
2. covariance_type: 协方差类型，包括 {‘full’,‘tied’, ‘diag’, ‘spherical’} 四种，full 指每个分量有各自不同的标准协方差矩阵，完全协方差矩阵（元素都不为零）， tied 指所有分量有相同的标准协方差矩阵（HMM 会用到），diag 指每个分量有各自不同对角协方差矩阵（非对角为零，对角不为零）， spherical 指每个分量有各自不同的简单协方差矩阵，球面协方差矩阵（非对角为零，对角完全相同，球面特性），默认‘full’ 完全协方差矩阵 
3. tol：EM 迭代停止阈值，默认为 1e-3. 
4. reg_covar: 协方差对角非负正则化，保证协方差矩阵均为正，默认为 0 
5. max_iter: 最大迭代次数，默认 100 
6. n_init: 初始化次数，用于产生最佳初始参数，默认为 1 
7. init_params: {‘kmeans’, ‘random’}, defaults to ‘kmeans’. 初始化参数实现方式，默认用 kmeans 实现，也可以选择随机产生 
8. weights_init: 各组成模型的先验权重，可以自己设，默认按照 7 产生 
9. means_init: 初始化均值，同 8 
10. precisions_init: 初始化精确度（模型个数，特征个数），默认按照 7 实现 
11. random_state : 随机数发生器 
12. warm_start : 若为 True，则 fit（）调用会以上一次 fit（）的结果作为初始化参数，适合相同问题多次 fit 的情况，能加速收敛，默认为 False。 
13. verbose : 使能迭代信息显示，默认为 0，可以为 1 或者大于 1（显示的信息不同） 
14. verbose_interval : 与 13 挂钩，若使能迭代信息显示，设置多少次迭代后显示信息，默认 10 次。

EM算法即最大期望算法（Expectation-Maximization algorithm, EM），是一类通过迭代进行极大似然估计（Maximum Likelihood Estimation, MLE）的优化算法，通常作为牛顿迭代法（Newton-Raphson method）的替代用于对包含隐变量（latent variable）或缺失数据（incomplete-data）的概率模型进行参数估计。

因其迭代规则容易实现并可以灵活考虑隐变量，EM算法被广泛应用于处理数据的缺失值，以及很多机器学习算法，包括高斯混合模型（Gaussian Mixture Model, GMM）和隐马尔可夫模型（Hidden Markov Model, HMM）的参数估计，是机器学习中使用最多的十大算法之一。

4.2 贝叶斯变分GMM模型

VBGMM的估计算法由变分推断（variational inference）替代EM算法，它是EM的拓展，它最大化了模型证据（包括先验）的下界，而不是数据的似然性。变分方法通过整合先验分布信息来增加正则化限制。 这避免了期望最大化解决方案中常出现的奇异性，但是也给模型带来了微小的偏差

由于它的贝叶斯特性，变分算法比预期最大化（EM）需要更多的超参数（即先验分布中的参数），其中最重要的就是浓度参数 weight_concentration_prior 。指定一个低浓度先验，将会使模型将大部分的权重分配到少数分量上，而其余分量的权重则趋近 0。而高浓度先验将会使混合模型中的更多的分量在混合模型中都有相当比列的权重。

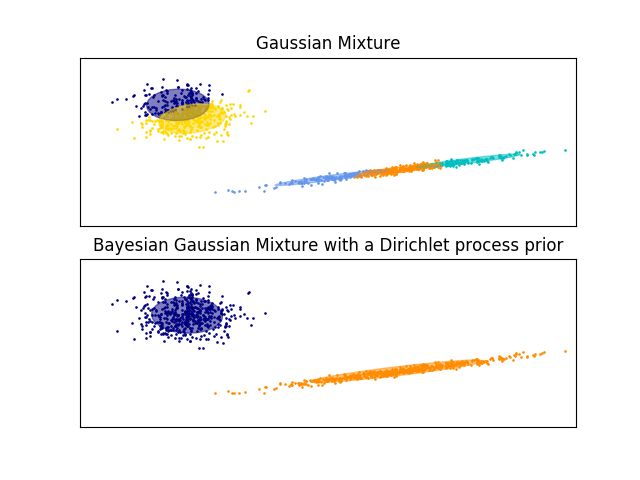
BayesianGaussianMixture 类的参数实现提出了两种权重分布先验： 一种是利用 Dirichlet distribution（狄利克雷分布）的有限混合模型，另一种是利用 Dirichlet Process（狄利克雷过程）的无限混合模型。在实际应用中，狄利克雷过程推理算法是近似的，并且使用具有固定最大分量数的截断分布（称之为 Stick-breaking representation）, 而其使用的分量数实际上总是依赖数据。

 变分推理的优缺点:

优点

• 自动选择: 当 weight_concentration_prior 足够小以及 n_components 比模型需要的数量更大时，变分贝叶斯混合模型计算的结果可以让一些混合权重值趋近 0。 这让模型可以自动选择合适的有效分量数量。这过程仅仅需要提供分量的数量上限。但是请注意，“理想” 的激活分量数量具有应用独特性，在数据挖掘参数设置中通常并不明确。
• 对参数数量的敏感度较低:
  和总是使用全部能用分量，因而由不同数量的分量来组合过量解决方案的有限模型不同, 带有狄利克雷过程先验的变分推理（weight_concentration_prior_type='dirichlet_process' ）的输出并不总拥有和参数一致的变化, 因此该变分推理更加稳定和需要更少的调优。
• 正则化: 由于结合了先验信息，变分的解比期望最大化（EM）的解有更少的病理特征（pathological special cases）。

缺点

• 速度: 变分推理所需要的额外参数化使推理速度变慢，尽管慢得不多。
• 超参数: 这个算法需要一个额外的可能需要交叉验证进行实验调优的超参数。
• 偏差: 在推理算法存在许多隐含的偏差（如果用到狄利克雷过程也会有偏差）， 每当这些偏差和数据之间不匹配时，用有限模型可能会拟合出更好的模型。

决策树算法

采用自顶向下的递归的方法，基本思想是以信息熵为度量构造一棵熵值下降最快的树，到叶子节点处熵值为0（叶节点中的实例都属于一类）。其基于数据的Rank排序，无需标准化、归一化。

• 决策树算法包括：ID3、C4.5、CART、GBDT、RF、DART、lambdaMART、XGBoost、lightGBM等
• ID3、C4.5、CART的内容主要是针对分类树最优属性的选取方法（信息纯度|基尼系数）
• 回归树最优属性的选取方法：梯度提升树GBT

DART（Dropouts meet Multiple Additive Regression Trees）

DART利用了深度神经网络中dropout设置的技巧，随机丢弃生成的决策树，然后再从剩下的决策树集中迭代优化提升树

lambdaMART

要介绍lambdaMART，我们就得先从RankNet说起。RankNet的实现既可以用神经网络来实现，也可以用决策树实现，总之它是将一个输入向量映射成一个实数。具体说来，给定一个数据集，而数据集是根据不同的query来划分的，对于每一个query，会有许多doc（查询的结果比如url等），这些doc自身的好坏我们不清楚，但是doc pair内与query谁更相关是已知的，这其实就是pair-wise。

那么RankNet所做的就是将doc所转换成的feature映射成一个实数（其实就是对这个doc打分）
根据各个doc的分数，我们可以算出doc pair内一种偏序概率，通过这个算出来的概率来计算损失。

lambdaMART与GBDT的不同之处在于将残差换为了λ，也就是说对每个样本（doc i），我们都求出它的λ，这个就是梯度，然后后面跟GBDT的算法基本一致，只不过加了二次优化。

XGBoost

残差累积boosting，XGBoost实际上就是在GBDT基础上加了二次优化和正则项

从决策树到XGBoost - 知乎

代码

XGBoost 重要参数、方法、函数理解及调参思路（附例子） - 灰信网（软件开发博客聚合）

史上最详细的XGBoost实战 - 知乎

lightGBM

LGBM主要是利用了大梯度单边采样、互斥特征绑定、直方图算法、leaf-wise策略等技巧使得训练速度大幅提升，内存消耗大量减少。

References

---

用于数据挖掘的聚类算法有哪些，各有何优势？_I-Love-IT的博客-CSDN博客_数据挖掘算法有哪些

Logistic（逻辑）回归分析_Jalen data analysis的博客-CSDN博客_logistic回归分析

一文详解高斯混合模型原理 - 知乎

[译] 高斯混合模型 --- python教程

决策树的进化（ID3、C4.5、CART、GBDT、RF、DART、lambdaMART、XGBoost、lightGBM）_strivinging的博客-CSDN博客_dart xgboost