机器学习之熵笔记
机器学习之熵笔记
- 1.物理学中的熵
- 2.信息论中的熵
-
- 2.1自信息
- 2.2信息熵
- 2.3联合信息熵
- 2.4条件熵
- 2.5互信息
- 2.6交叉熵
- 2.7相对熵
- 2.8信息增益
- 2.9信息增益率
- 2.10基尼系数
1.物理学中的熵
19世纪,物理学家开始认识到,世界的动力是能量,并且提出 能量守恒定律,即能量的总和是不变的。但是,有一个现象让他们很困惑。物理学家发现,能量无法百分百地转换。比如,蒸汽机使用的是热能,将其转换为推动机器的机械能。这个过程中,总是有一些热能损耗掉,无法完全转变为机械能。一开始,物理学家以为是技术水平不高导致的,但后来发现,技术再进步,也无法将能量损耗降到零。他们就将那些在能量转换过程中浪费掉的、无法再利用的能量称为 熵。
后来,这个概念被总结成了 热力学第二定律:能量转换总是会产生熵,如果是封闭系统,所有能量最终都会变成熵。
熵描述的是混乱程度,熵越大则系统越混乱。通过几个例子来具体了解熵与混乱之间的关系:
1、我们长期居住在一个房子里,房间如果没人打扫,只会越来越乱,垃圾到处都是,不可能越来越干净。如果想要改变这混乱的房间,必须打扫它,而打扫的过程,可理解为注入能量的过程。所以要使熵降低,就必须不断提供能量,保持房间的整洁。
2、我们每一个人,都可以看成一个系统,如果不给自己提供能量(不吃不喝)来维持自己的生命,体内的熵会逐渐变大,越来越混乱,直至死亡。
3、一杯清水,开始的时候纯度很高,现在向里面加入一滴蓝墨水,墨水会逐渐扩散到每一个分子的位置,这个过程可以看作熵逐渐增大的过程,水的纯度降低,系统逐渐混乱,充斥在每一个分子之间,最终变成一杯蓝水。
4、我们的宇宙,有很多发光发热的恒星,根据热力学第二定律,温度高的物体能量向温度低的物体传递,最终整个宇宙的温度会趋于平和,即宇宙任何地方的温度都一样,这时宇宙就会趋于死寂的状态。
以上的四个例子,都是随着时间的推移,物体的熵逐渐增大,系统越来越混乱的过程。当然混乱本身是一种感性词汇,或许有人认为,人的最终死亡是一种趋于平静,是一种确定性的趋向,并非趋于混乱。那么,请你将混乱理解为,宇宙万物,在没有外部能量的维持情况下,都是朝着灭亡发展的,即所谓的朝着熵增大,混乱无序的方向发展的。
物理学中波尔兹曼研究得到,热力学熵与微观状态数目的对数之间存在联系。其中, k k k为玻尔兹曼常数, W W W为微观状态的数目,公式为: S = k l o g W S = k\ logW S=k logW

2.信息论中的熵
2.1自信息
自信息又叫信息量,表示某一事件发生时所带来的信息量的多少,当事件发生的概率越大,则自信息越小。如:别人告诉你,明天太阳从东边升起。因为太阳从东边升起这个事件发生的概率很大,这个信息是显而易见的,所以此信息带给我们的信息量等于零。但是,如果告诉你,某个发达国家发动了政变,你就会震惊,想去看新闻,你就会感觉这个信息量有点大呀!这是从文字的角度理解,但是如何度量它呢?我们现在要寻找一个函数,它要满足的条件是:
- 事件发生的概率越大,则信息量越小。
- 自信息不能是负值,最小是0。这个很好理解,因为获得一个信息,最多是此信息对你没有任何用处,不会因为得知了一个信息,记忆反而被删除了。在正常情况下,这是不符合逻辑的。
- 自信息应该满足可加性,随着知道的信息越多,信息量是逐渐增加的。并且多个独立事件的信息量应该等于多个事件单独的信息量之和。
于是,找到一个满足上述条件的函数,下面给出自信息的具体公式: I ( p i ) = − l o g p i I(p_i)=-log \ p_i I(pi)=−log pi或表示为 I ( X ) = − l o g p ( x ) I(X)=-log \ p(x) I(X)=−log p(x)其中 l o g log log可以是以2为底,也可以是以 e e e为底等等,默认以2为底。 p i p_i pi为事件发生的概率,自信息的单位是 bit(比特),函数图像如下:
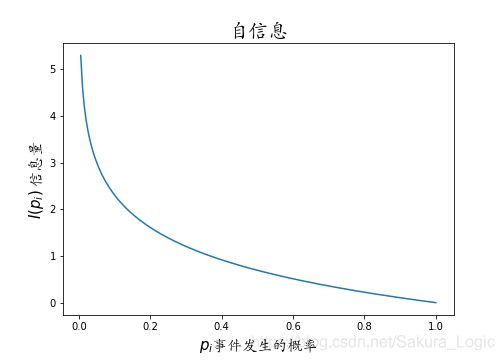 自信息是基于概率的函数,概率有联合概率、条件概率等。类比自信息也有联合自信息与条件自信息。联合自信息公式: I ( X , Y ) = − l o g p ( x , y ) I(X,Y)=-log \ p(x,y) I(X,Y)=−log p(x,y)条件自信息公式: I ( Y ∣ X ) = − l o g p ( y ∣ x ) I(Y|X)=-log \ p(y|x) I(Y∣X)=−log p(y∣x)后面要说的信息熵,联合信息熵与条件信息熵,都是由一系列的自信息得到的。
自信息是基于概率的函数,概率有联合概率、条件概率等。类比自信息也有联合自信息与条件自信息。联合自信息公式: I ( X , Y ) = − l o g p ( x , y ) I(X,Y)=-log \ p(x,y) I(X,Y)=−log p(x,y)条件自信息公式: I ( Y ∣ X ) = − l o g p ( y ∣ x ) I(Y|X)=-log \ p(y|x) I(Y∣X)=−log p(y∣x)后面要说的信息熵,联合信息熵与条件信息熵,都是由一系列的自信息得到的。
2.2信息熵
信息熵反应的是任何一种能量在空间中分布的均匀程度,分布越均匀,信息熵的值就越大。上述,一系列自信息都是针对判断一个事件带来的信息量。如: P P P(明天下雨的概率) = 0.7 =0.7 =0.7, P P P(明天不下雨的概率) = 0.3 =0.3 =0.3,可以将这两种情况分别代入公式 I ( p i ) = − l o g ( p i ) I(p_i)=-log(p_i) I(pi)=−log(pi),求出各自的自信息。如果想要知道,明天雨晴情况这一整体事件的信息量呢!大家都会想到,把每一种情况逐步带入自信息公式 I ( p i ) = − l o g ( p i ) I(p_i)=-log(p_i) I(pi)=−log(pi),然后再求平均,用平均数说明问题。
通过上述的推论,你可能认为信息熵的公式应该是这样的, H ( X ) = − 1 N ∑ i = 1 N l o g ( p i ) H(X) =- \frac{1}{N}\sum_{i=1}^{N}log(p_i) H(X)=−N1∑i=1Nlog(pi),但显然信息熵的公式不是这样的。在学习概率论与数理统计中了解到,这种把所有情况相加起来除以个数的表达,只是样本均值,而不是总体均值。那什么是总体均值,或为什么用总体均值呢。总体均值就是我们所说的数学期望。从字面意思就可以理解,样本是在总体中选出来的一部分,这部分值只是总体的部分代表,而没有充分的考虑整体样本的特性。而总体均值,兼顾的考虑到元素值的分布率(每个值出现的概率),更具有对大数据的统计性(特殊的,如果总体是均匀的,即整体特性与任意样本特性一致,如等可能的古典概型。那么任意取一部分完备样本,此样本的均值与总体均值一致)。对于广义上的统计数据来说,根据大数定律,只要样本取的足够大,这时候样本均值(算数平均数)最终将会等于总体均值(数学期望)。大概介绍到这里,详细的请参考概率论与数理统计中的大数定律。总之,可以理解为样本均值与总体均值(数学期望)本质都是求平均数。显然,信息熵用的是,总体均值(数学期望)。
所以,也就相当于求自信息的数学期望,即 H ( X ) = E [ I ( X ) ] H(X)=E[I(X)] H(X)=E[I(X)]根据数学期望公式,离散情况下得: E ( p ) = − ∑ i = 1 N p i l o g p i E(p) =- \sum_{i=1}^{N}p_i\ log \ p_i E(p)=−i=1∑Npi log pi或写成 H ( X ) = − ∑ x p ( x ) l o g p ( x ) H(X) =- \sum_{x}p(x)\ log \ p(x) H(X)=−x∑p(x) log p(x)
连续情况下得, E ( p ) = − ∫ p i l o g p i E(p)=-\int p_ilog \ p_i E(p)=−∫pilog pi或写成 H ( X ) = − ∫ X p ( x ) l o g p ( x ) d x H(X)=-\int_X p(x)log \ p(x)dx H(X)=−∫Xp(x)log p(x)dx
下面来介绍一下这个函数的图像,因为 H ( X ) H(X) H(X)是个累加的函数,函数值一定和累加的次数有关,为了方便表示其图像轮廓,就以离散型抛硬币为例来说明一下。抛硬币有两个结果,所以 N N N取为2。分别为 p p p(正面向上) = 1 2 =\frac{1}{2} =21 和 p p p(反面向上) = 1 2 =\frac{1}{2} =21 ,代入信息熵公式 H ( X ) = − 1 2 l o g 1 2 − 1 2 l o g 1 2 = l o g 2 = 1 H(X)=-\frac{1}{2}log\frac{1}{2}-\frac{1}{2}log\frac{1}{2}=log2=1 H(X)=−21log21−21log21=log2=1,这能说明什么呢?其实,对于抛硬币来说,这就是熵最大的时候,也就是最混乱的时候。就是因为,正面和反面的概率是一样的,我们猜哪一面都不太确定,没有比这再糟糕的了。比如,再告诉你这个硬币改造了一下,它正面的概率为 2 3 \frac{2}{3} 32,反面的概率为 1 3 \frac{1}{3} 31,此时的熵 H ( X ) = − 2 3 l o g 2 3 − 1 3 l o g 1 3 = 0.2783 H(X)=-\frac{2}{3}log\frac{2}{3}-\frac{1}{3}log\frac{1}{3}=0.2783 H(X)=−32log32−31log31=0.2783,这种情况下熵就变小了,不确定性也变小了,此时我们比较确定会是正面;又或者告诉你,这个硬币又改造了一下,它正面的概率为 0 0 0,反面的概率为 1 1 1,此时的熵 H ( X ) = − 0 l o g 0 − 1 l o g 1 = 0 H(X)=-0log0-1log1=0 H(X)=−0log0−1log1=0,熵最低,不确定性完全没了,一定是反面了;发现没有,只要概率不是均等的,我们总会更确定一些,选出概率相对大的。从这个角度可以看出,在概率为等可能的情况下,就是熵值最大的时候。
同样,现在置筛子,有六种结果,此时 N N N为6,熵最大的时候为等可能的情况,即 H ( X ) = − 1 6 l o g 1 6 − 1 6 l o g 1 6 − 1 6 l o g 1 6 − 1 6 l o g 1 6 − 1 6 l o g 1 6 − 1 6 l o g 1 6 = l o g 6 H(X)=-\frac{1}{6}log\frac{1}{6}-\frac{1}{6}log\frac{1}{6}-\frac{1}{6}log\frac{1}{6}-\frac{1}{6}log\frac{1}{6}-\frac{1}{6}log\frac{1}{6}-\frac{1}{6}log\frac{1}{6}=log6 H(X)=−61log61−61log61−61log61−61log61−61log61−61log61=log6。无论是哪一种情况,熵最小的时候都是概率取0和1的时候,这个可以通过公式证明,因为 p ( x ) p(x) p(x)表示的是一种概率,所以自变量 p ( x ) p(x) p(x)取值为 0 < = p ( x ) < = 1 0<=p(x)<=1 0<=p(x)<=1。当概率取0使,利用极限求得 lim p ( x ) → 0 H ( X ) = lim p ( x ) → 0 p ( x ) l o g p ( x ) = 0 \mathop{\lim}_{p(x) \to 0 }H(X)=\mathop{\lim}_{p(x) \to 0 }p(x) logp(x)=0 limp(x)→0H(X)=limp(x)→0p(x)logp(x)=0;同样当概率 p ( x ) p(x) p(x)取1时,可直接求得 H ( X ) = p ( x ) l o g p ( x ) = 0 H(X)=p(x) logp(x)=0 H(X)=p(x)logp(x)=0。尽管 H ( X ) H(X) H(X)是个累加的函数,因为两种结果都是0,所以即使累加后结果还是0。
通过上面的两个例子,发现信息熵的最大值与事件可能性的个数有关,即与 N N N有关,为 l o g N logN logN。所以基本通过描点作图法得到函数 H ( x ) H(x) H(x)的取值范围为: 0 ⩽ X ⩽ l o g N 0 \leqslant X \leqslant logN 0⩽X⩽logN 。其中 N N N为事件所有可能的结果数,信息熵的单位是bit/信源符号。
信息熵的函数图像如下:
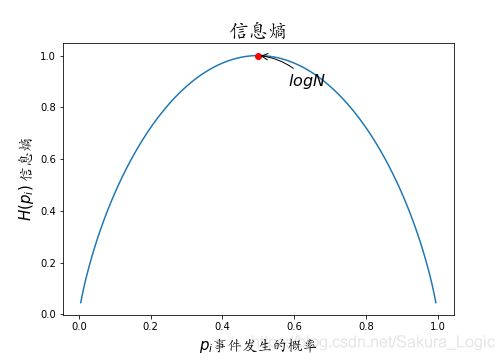
为了更好的理解自信息与信息熵的关系,还可以将自信息比作一发子弹的威力。则信息熵就是所有子弹威力的平均,即整把枪的性能。自信息的单位是 bit(比特),信息熵的单位是bit/信源符号。可以看出,信息熵的单位是基于自信息。
最后,有同学可能会发现,上述的两个古典概型例子(投硬币和置筛子),代入最开始说的样本均值下的信息熵 H ( X ) = − 1 N ∑ i = 1 N l o g ( p i ) H(X) =- \frac{1}{N}\sum_{i=1}^{N}log(p_i) H(X)=−N1∑i=1Nlog(pi)的结果和代入总体均值下真正的信息熵的公式结果是一样的。又间接的说明了样本均值与总体均值的关系,在不考虑元素分布率的情况下(即每个样本都是等可能的),这种古典概型中样本均值的适用性。
2.3联合信息熵
同样,联合信息熵是对联合自信息取总体平均值(数学期望), H ( X , Y ) = E [ I ( X , Y ) ] H(X, Y)=E[I(X,Y)] H(X,Y)=E[I(X,Y)],根据数学期望公式,联合信息熵为: H ( X , Y ) = − ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( x i , y j ) H(X,Y)=-\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)logp(x_i,y_j) H(X,Y)=−i=1∑Nj=1∑Mp(xi,yj)logp(xi,yj) 可以用班级学生为例,一个班级有6个学生,此时 p ( x i ) p(x_i) p(xi)表示成绩,成绩有优中差三类,所以 N N N就为3; p ( y j ) p(y_j) p(yj)表示是三好学生,三好学生有是否两类,所以 M M M取2;则联合概率 P ( x i , y j ) P(x_i,y_j) P(xi,yj)表示同时取成绩和是否为三好学生.。联合概率分布 P ( x i , y j ) P(x_i,y_j) P(xi,yj)包含了同时取两种属性的所有可能的组合,整体上表示为并集。具体到特定值,如: P ( x 中 , y 是 ) P(x_中,y_是) P(x中,y是)则表示成绩为中等并且是三好学生的概率,为两者的交集。
| 成绩 | 是否为三好学生 | |
|---|---|---|
| 学生一 | 优 | 是 |
| 学生二 | 优 | 是 |
| 学生三 | 中 | 是 |
| 学生四 | 中 | 否 |
| 学生五 | 差 | 否 |
| 学生六 | 差 | 否 |
2.4条件熵
条件熵与上面略有不同。具体定义为,在X给定条件下,Y的条件概率分布的熵对X的数学期望。相当于是对条件自信息求完数学期望,再对其结果求关于X的数学期望。公式为: H ( Y ∣ X ) = ∑ i = 1 N p ( x i ) E ( I ( Y ∣ X ) ) = − ∑ i = 1 N p ( x i ) ∑ j = 1 M p ( y j ∣ x i ) l o g p ( y j ∣ x i ) = − ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( y j ∣ x i ) = − ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( x i , y j ) p ( x i ) = − ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( x i , y j ) + ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( x i ) = H ( X , Y ) − [ − ∑ i = 1 N p ( x i ) l o g p ( x i ) ] = H ( X , Y ) − H ( X ) \begin{aligned} H(Y|X) &= \sum_{i=1}^{N}p(x_i)E(I(Y|X)) \\ & = -\sum_{i=1}^{N}p(x_i) \sum_{j=1}^{M} p(y_j|x_i)log p(y_j|x_i)\\ &=-\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)log p(y_j|x_i) \\ & = -\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)log \frac{p(x_i,y_j)}{p(x_i)} \\ & = -\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)logp(x_i,y_j)+\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)logp(x_i) \\ & = H(X,Y)-[-\sum_{i=1}^{N}p(x_i)logp(x_i)] \qquad \\ &=H(X,Y)-H(X) \end{aligned} H(Y∣X)=i=1∑Np(xi)E(I(Y∣X))=−i=1∑Np(xi)j=1∑Mp(yj∣xi)logp(yj∣xi)=−i=1∑Nj=1∑Mp(xi,yj)logp(yj∣xi)=−i=1∑Nj=1∑Mp(xi,yj)logp(xi)p(xi,yj)=−i=1∑Nj=1∑Mp(xi,yj)logp(xi,yj)+i=1∑Nj=1∑Mp(xi,yj)logp(xi)=H(X,Y)−[−i=1∑Np(xi)logp(xi)]=H(X,Y)−H(X) ( 注 : 上 述 过 程 中 ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) = ∑ i = 1 N p ( x i ) , 因 为 联 合 概 率 之 和 等 于 边 缘 概 率 ) (注:上述过程中\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)=\sum_{i=1}^{N}p(x_i),因为联合概率之和等于边缘概率) (注:上述过程中i=1∑Nj=1∑Mp(xi,yj)=i=1∑Np(xi),因为联合概率之和等于边缘概率)
同样可以得到 H ( X ∣ Y ) = H ( X , Y ) − H ( Y ) H(X|Y)=H(X,Y)-H(Y) H(X∣Y)=H(X,Y)−H(Y)
2.5互信息
在概率论和信息论中,两个随机变量的互信息(Mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布 p(X,Y) 和边缘概率分布 p(X)p(Y) 的相似程度。互信息是度量两个事件集合之间的相关性(mutual dependence)。互信息最常用的单位是bit。离散情况下互信息: I ( x , y ) = ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g ( p ( x i , y j ) p ( x i ) p ( y j ) ) I(x,y)= \sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)log(\frac{p(x_i,y_j)}{p(x_i)p(y_j)}) I(x,y)=i=1∑Nj=1∑Mp(xi,yj)log(p(xi)p(yj)p(xi,yj)) 连续情况下互信息: I ( X , Y ) = ∫ X ∫ Y p ( x , y ) l o g ( p ( x , y ) p ( x ) p ( y ) ) d x d y I(X,Y)=\int_X\int_Yp(x,y)log(\frac{p(x,y)}{p(x)p(y)})dxdy I(X,Y)=∫X∫Yp(x,y)log(p(x)p(y)p(x,y))dxdy直观上,互信息度量 X 和 Y 共享的信息,它度量知道这两个变量其中的一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,即 p ( x , y ) = p ( x ) p ( y ) p(x,y)=p(x)p(y) p(x,y)=p(x)p(y)。则知道 X 不对 Y 提供任何信息,所以它们的互信息为零。从公式中可以看出 l o g ( p ( x , y ) p ( x ) p ( y ) ) = l o g 1 = 0 log(\frac{p(x,y)}{p(x)p(y)})=log1=0 log(p(x)p(y)p(x,y))=log1=0在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y 共享,此时X与Y的互信息就等于X的熵,也等于Y的熵。
互信息可以看作为:一个随机变量由于已知另一个随机变量而减少的不确定性,或者说从贝叶斯角度考虑,由于新的观测数据y到来而导致x分布的不确定性下降程度。
如图,互信息与其它熵之间的关系:

由图可以直接得到关系式: I ( X , Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X , Y ) = H ( X , Y ) − H ( X ∣ Y ) − H ( Y ∣ X ) \begin{aligned} I(X,Y) &= H(X)-H(X|Y) \\ & = H(Y)-H(Y|X)\\& =H(X)+H(Y)-H(X,Y)\\& =H(X,Y)-H(X|Y)-H(Y|X)\\ \end{aligned} I(X,Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)=H(X,Y)−H(X∣Y)−H(Y∣X) 以公式的角度推导:
I ( X , Y ) = ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g ( p ( x i , y j ) p ( x i ) p ( y j ) ) = ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g ( p ( x i , y j ) p ( x i ) ) − ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) l o g p ( y j ) = ∑ i = 1 N ∑ j = 1 M p ( x i ) p ( y i ∣ x i ) l o g p ( y i ∣ x i ) − ∑ j = 1 M p ( y j ) l o g p ( y j ) ] = H ( Y ) − H ( Y ∣ X ) \begin{aligned} I(X,Y) &=\sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)log(\frac{p(x_i,y_j)}{p(x_i)p(y_j)}) \\ & = \sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)log(\frac{p(x_i,y_j)}{p(x_i)})- \sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)logp(y_j)\\& = \sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i)p(y_i|x_i)logp(y_i|x_i)-\sum_{j=1}^{M}p(y_j)logp(y_j)]\\& =H(Y)-H(Y|X)\\ \end{aligned} I(X,Y)=i=1∑Nj=1∑Mp(xi,yj)log(p(xi)p(yj)p(xi,yj))=i=1∑Nj=1∑Mp(xi,yj)log(p(xi)p(xi,yj))−i=1∑Nj=1∑Mp(xi,yj)logp(yj)=i=1∑Nj=1∑Mp(xi)p(yi∣xi)logp(yi∣xi)−j=1∑Mp(yj)logp(yj)]=H(Y)−H(Y∣X) 对于上述推导,仅证明 I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) I(X,Y)=H(Y)-H(Y|X) I(X,Y)=H(Y)−H(Y∣X)。且用到了,联合概率之和等于边缘概率,即 ∑ i = 1 N ∑ j = 1 M p ( x i , y j ) = ∑ i = 1 N p ( x i ) = ∑ j = 1 M p ( y j ) \sum_{i=1}^{N}\sum_{j=1}^{M}p(x_i,y_j)=\sum_{i=1}^{N}p(x_i)=\sum_{j=1}^{M}p(y_j) i=1∑Nj=1∑Mp(xi,yj)=i=1∑Np(xi)=j=1∑Mp(yj) 如果把熵 H ( Y ) H(Y) H(Y) 看作一个随机变量不确定度的量度,那么 H ( Y ∣ X ) H(Y|X) H(Y∣X) 就是 X X X 没有涉及到的 Y Y Y 的部分的不确定度的量度。这就是“在 X X X 已知之后 Y Y Y 的剩余不确定度的量”,于是最后等式的右边就可以读作“ Y Y Y的不确定度,减去在 X X X 已知之后 Y Y Y 的剩余不确定度的量”,此式等价于“移除知道 X X X 后 Y Y Y 的不确定度的量”。这证实了互信息的直观意义为知道其中一个变量提供的另一个的信息量(即不确定度的减少量)。
注意到离散情形 H ( X ∣ X ) = 0 H(X|X) = 0 H(X∣X)=0,于是 H ( X ) = I ( X , X ) H(X) = I(X,X) H(X)=I(X,X)。因此 I ( X , X ) ≥ I ( X , Y ) I(X,X) ≥ I(X,Y) I(X,X)≥I(X,Y),我们可以制定”一个变量至少包含其他任何变量可以提供的与它有关的信息“的基本原理。
互信息和相对熵也存在联系,如果说相对熵不能作为距离度量,是因为其非对称性,那么互信息的出现正好弥补了该缺陷,使得我们可以计算任意两个随机变量之间的距离,或者说两个随机变量分布之间的相关性、独立性。关系式如下: I ( X , Y ) = K L ( p ( x , y ) ∣ ∣ p ( x ) p ( y ) ) I(X,Y)=KL(p(x,y)||p(x)p(y)) I(X,Y)=KL(p(x,y)∣∣p(x)p(y))互信息也是大于等于 0 0 0 的,当且仅当 x x x 与 y y y 相互独立时候取等号。
2.6交叉熵
交叉熵主要用于度量两个概率分布间的差异性信息, p p p 对 q q q 的交叉熵表示 q q q 分布的自信息对 p p p 分布的期望, p p p 是真实样本分布, q q q 是预测得到样本分布公式定义为: H ( p , q ) = E x ∼ p [ − l o g q ( x ) ] = − ∑ i = 1 N p ( x i ) l o g q ( x i ) H(p,q)=E_{x\sim p}[-logq(x)]=-\sum_{i=1}^{N}p(x_i)logq(x_i) H(p,q)=Ex∼p[−logq(x)]=−i=1∑Np(xi)logq(xi) 逻辑回归算法的损失函数就是交叉熵,也叫做负对数似然,公式为: J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ] J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})] J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))]其中, y i y_i yi是第 i i i个样本的真实标签, h θ ( x ) h_\theta(x) hθ(x) 是 sigmoid 预测输出值, J ( θ ) J(\theta) J(θ)是(Convex Function)凸函数,可以得到全局最优解。
2.7相对熵
相对熵(relative entropy),又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是两个概率分布(probability distribution)间差异的非对称性度量 。在信息理论中,相对熵等价于两个概率分布的信息熵(Shannon entropy)的差值。相对熵是一些优化算法,例如最大期望算法(Expectation-Maximization algorithm, EM)的损失函数。此时参与计算的一个概率分布为真实分布,另一个为理论(拟合)分布,相对熵表示使用理论分布拟合真实分布时产生的信息损耗。
相对熵经常也叫做KL散度,在贝叶斯推理中, D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q)衡量当你修改了从先验分布 q q q 到后验分布 p p p 的信念之后带来的信息增益。首先给出其连续和离散的公式: D K L ( p ∣ ∣ q ) = E x ∼ p [ l o g p ( x ) q ( x ) ] = − ∫ x p ( x ) l o g q ( x ) p ( x ) = − ∑ i = 1 N p ( x i ) l o g q ( x i ) p ( x i ) = H ( p , q ) − H ( p ) \begin{aligned} D_{KL}(p||q) &= E_{x \sim p}[log \frac{p(x)}{q(x)}] \\ & =-\int_xp(x)log \frac{q(x)}{p(x)} \\ & =-\sum_{i=1}^{N}p(x_i)log \frac{q(x_i)}{p(x_i)}\\& =H(p,q)-H(p) \\ \end{aligned} DKL(p∣∣q)=Ex∼p[logq(x)p(x)]=−∫xp(x)logp(x)q(x)=−i=1∑Np(xi)logp(xi)q(xi)=H(p,q)−H(p) 相对熵较交叉熵有更多的优异性质,主要为:
- 当p分布和q分布相等时候,KL散度值为0;
- 可以证明是非负的,证明方式利用Jensen不等式;
- 非对称的,通过公式可以看出, K L KL KL 散度是衡量两个分布的不相似性,不相似性越大,则值越大,当完全相同时,取值为 0 0 0。
简单对比交叉熵和相对熵,可以发现仅仅差了一个 H ( p ) H(p) H(p),如果从优化角度来看, p p p是真实分布,是固定值,最小化KL散度情况下, H ( p ) H(p) H(p)可以省略,此时交叉熵等价于 K L KL KL散度。既然相对熵和交叉熵表示的含义一样,为啥需要两个?在机器学习中何时使用相对熵,何时使用交叉熵?首先需要明确:在最优化问题中,最小化相对熵等价于最小化交叉熵;相对熵和交叉熵的定义其实都可以从最大似然估计得到。
下面进行详细推导:以某个生成模型算法为例,假设是生成对抗网络 G A N GAN GAN,其实只要是生成模型,都满足以下推导。若给定一个样本数据的真实分布 P d a t a ( x ) P_{data}(x) Pdata(x)和生成的数据分布 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ),那么生成模型希望能找到一组参数θ使分布 P d a t a ( x ) P_{data}(x) Pdata(x)和 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ)之间的距离最短,也就是找到一组生成器参数而使得生成器能生成十分逼真的分布。现在从真实分布 P d a t a ( x ) P_{data}(x) Pdata(x)中抽取N个真实样本 x 1 , x 2 , … , x N x^1,x^2,\dots,x^N x1,x2,…,xN,对于每一个真实样本,我们可以计算 P G ( x i ; θ ) P_{G}(x^i;\theta) PG(xi;θ)即在由 θ θ θ确定的生成分布中, x i x^i xi样本所出现的概率。因此,我们可以构建似然函数: L = ∏ i = 1 N P G ( x i ; θ ) L=\prod_{i=1}^{N}P_{G}(x^i;\theta) L=i=1∏NPG(xi;θ)最大化似然函数,即可求得最优参数 θ ∗ \theta^* θ∗ :
θ ∗ = a r g m a x ⏟ θ ∏ i = 1 N P G ( x i ; θ ) \begin{matrix} \theta^*=arg \ \mathop{\underbrace{max}}\limits_{\theta} \prod_{i=1}^{N} P_{G}(x^i;\theta)\\ \end{matrix} θ∗=arg θ max∏i=1NPG(xi;θ) 转化为对数似然函数: θ ∗ = a r g m a x ⏟ θ l o g ∏ i = 1 N P G ( x i ; θ ) = a r g m a x ⏟ θ ∑ i = 1 N l o g P G ( x i ; θ ) \begin{aligned} \theta^* &= arg \ \mathop{\underbrace{max}}\limits_{\theta} log\prod_{i=1}^{N} P_{G}(x^i;\theta) \\ & =arg \ \mathop{\underbrace{max}}\limits_{\theta} \sum_{i=1}^{N}log P_{G}(x^i;\theta) \\ \end{aligned} θ∗=arg θ maxlogi=1∏NPG(xi;θ)=arg θ maxi=1∑NlogPG(xi;θ) 由于是求最大值,故整体乘上常数对结果没有影响,这里是逐点乘上一个常数,所以不能取等于号,但是因为在取得最大值时候 P G ( x i ; θ ∗ ) P_{G}(x^i;\theta^*) PG(xi;θ∗) 和 P d a t a ( x ) P_{data}(x) Pdata(x)肯定是相似的,并且肯定大于0,所以依然可以认为是近视相等的: θ ∗ ≈ a r g m a x ⏟ θ ∑ i = 1 N P d a t a ( x i ) l o g P G ( x i ; θ ) = a r g m a x ⏟ θ E x ∼ P d a t a [ l o g P G ( x i ; θ ) ] \begin{aligned}\theta^* & \approx arg \ \mathop{\underbrace{max}}\limits_{\theta} \sum_{i=1}^{N} P_{data}(x^i)log P_{G}(x^i;\theta) \\ &=arg \ \mathop{\underbrace{max}}\limits_{\theta} E_{x \sim P_{data}}[logP_{G}(x^i;\theta)] \\ \end{aligned} θ∗≈arg θ maxi=1∑NPdata(xi)logPG(xi;θ)=arg θ maxEx∼Pdata[logPG(xi;θ)] 上面的公式正好是交叉熵的定义式。然后我们再该基础上减掉一个常数: θ ∗ = a r g m a x ⏟ θ ( E x ∼ P d a t a [ l o g P G ( x i ; θ ) ] − E x ∼ P d a t a [ l o g P d a t a ( x i ) ] ) = a r g m a x ⏟ θ ∫ x P d a t a ( x ) l o g P G ( θ ) P d a t a d x = a r g m i n ⏟ θ ∫ x P d a t a ( x ) l o g P d a t a P G ( θ ) d x = a r g m i n ⏟ θ E x ∼ P d a t a [ l o g P d a t a P G ( θ ) ] = a r g m i n ⏟ θ K L ( P d a t a ( x ) ∣ ∣ P G ( x ; θ ) ) \begin{aligned}\theta^* &=arg \ \mathop{\underbrace{max}}\limits_{\theta} (E_{x \sim P_{data}}[logP_{G}(x^i;\theta)]-E_{x \sim P_{data}}[logP_{data}(x^i)] )\\ &=arg \ \mathop{\underbrace{max}}\limits_{\theta} \ \int_xP_{data}(x) \ log \frac{P_G(\theta)}{P_{data}}dx \\&=arg \ \mathop{\underbrace{min}}\limits_{\theta} \ \int_xP_{data}(x) \ log \frac{P_{data}}{P_G(\theta)}dx \\ &= arg \ \mathop{\underbrace{min}}\limits_{\theta} E_{x \sim P_{data}}[log \frac{P_{data}}{P_G(\theta)}] \\ &=arg \ \mathop{\underbrace{min}}\limits_{\theta} KL(P_{data}(x)||P_{G}(x;\theta)) \end{aligned} θ∗=arg θ max(Ex∼Pdata[logPG(xi;θ)]−Ex∼Pdata[logPdata(xi)])=arg θ max ∫xPdata(x) logPdataPG(θ)dx=arg θ min ∫xPdata(x) logPG(θ)Pdatadx=arg θ minEx∼Pdata[logPG(θ)Pdata]=arg θ minKL(Pdata(x)∣∣PG(x;θ)) 通过以上各公式可以得出以下结论:最大化似然函数,等价于最小化负对数似然,等价于最小化交叉熵,等价于最小化KL散度。
交叉熵大量应用在Sigmoid函数和SoftMax函数中,最典型的算法应该就是神经网络和逻辑回归,而相对熵大量应用在生成模型中,例如GAN、EM、贝叶斯学习和变分推导中。从这里我们可以看出一些端倪,如果想通过算法对样本数据进行概率分布建模,那么通常都是使用相对熵,因为我们需要明确的知道生成的分布和真实分布的差距,最好的KL散度值应该是0;而在判别模型中,仅仅只需要评估损失函数的下降值即可,交叉熵可以满足要求,其计算量比KL散度小。在数学之美书中,有这样几句话:交叉熵,其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小,相对熵,其用来衡量两个取值为正的函数或概率分布之间的差异。
证明相对熵非负 D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q) \ge 0 DKL(p∣∣q)≥0,即证 − D K L ( p ∣ ∣ q ) ≤ 0 -D_{KL}(p||q) \le 0 −DKL(p∣∣q)≤0。这个证明主要用到了Jensen不等式,因为 l o g x logx logx函数为concave函数,满足Jensen不等式中 E [ l o g ( x ) ] ≤ l o g ( E [ x ] ) E[log(x)] \le log(E[x]) E[log(x)]≤log(E[x]): − D K L ( p ∣ ∣ q ) = − E x ∼ p [ l o g p ( x ) q ( x ) ] = ∑ i = 1 N p ( x i ) l o g q ( x i ) p ( x i ) ≤ l o g ∑ i = 1 N p ( x i ) q ( x i ) p ( x i ) = l o g ∑ i = 1 N q ( x i ) = l o g 1 = 0 \begin{aligned} -D_{KL}(p||q) &= -E_{x \sim p}[log \frac{p(x)}{q(x)}] \\ & =\sum_{i=1}^{N}p(x_i)log \frac{q(x_i)}{p(x_i)}\\& \le log\sum_{i=1}^{N}p(x_i)\frac{q(x_i)}{p(x_i)} \\ &=log\sum_{i=1}^{N} q(x_i)=log1=0 \end{aligned} −DKL(p∣∣q)=−Ex∼p[logq(x)p(x)]=i=1∑Np(xi)logp(xi)q(xi)≤logi=1∑Np(xi)p(xi)q(xi)=logi=1∑Nq(xi)=log1=0 所以, D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q) \ge0 DKL(p∣∣q)≥0 证明相对熵非负的另一种方法,利用函数关系证明:
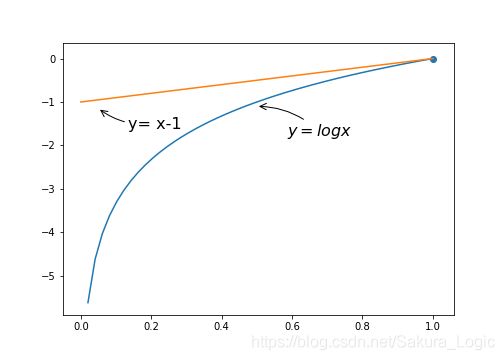
从上图中可以看出,再 x ∈ ( 0 , 1 ] x \in (0,1] x∈(0,1]时, l o g ( x ) ≤ x − 1 log(x) \le x-1 log(x)≤x−1,当 x = 1 x=1 x=1时取等。将不等式同样带入负的相对熵: − D K L ( p ∣ ∣ q ) = ∑ i = 1 N p ( x i ) l o g q ( x i ) p ( x i ) ≤ ∑ i = 1 N p ( x i ) ( q ( x i ) p ( x i ) − 1 ) = ∑ i = 1 N q ( x i ) − ∑ i = 1 N p ( x i ) = 0 \begin{aligned} -D_{KL}(p||q) &=\sum_{i=1}^{N}p(x_i)log \frac{q(x_i)}{p(x_i)}\\& \le \sum_{i=1}^{N}p(x_i)(\frac{q(x_i)}{p(x_i)}-1) \\ &=\sum_{i=1}^{N} q(x_i)-\sum_{i=1}^{N} p(x_i)=0 \end{aligned} −DKL(p∣∣q)=i=1∑Np(xi)logp(xi)q(xi)≤i=1∑Np(xi)(p(xi)q(xi)−1)=i=1∑Nq(xi)−i=1∑Np(xi)=0 所以, D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q) \ge0 DKL(p∣∣q)≥0 上述两个证明,最后都用到了自身全概率为1,即 ∑ i = 1 N q ( x i ) = ∑ i = 1 N p ( x i ) = 1 \sum_{i=1}^{N} q(x_i)=\sum_{i=1}^{N} p(x_i)=1 ∑i=1Nq(xi)=∑i=1Np(xi)=1
2.8信息增益
信息增益(Kullback–Leibler divergence)又称information divergence,information gain,relative entropy 或者KLIC。在概率论和信息论中,信息增益是非对称的,用以度量两种概率分布 P P P 和 Q Q Q 的差异。信息增益描述了当使用 Q Q Q 进行编码时,再使用P进行编码的差异。通常 P P P 代表样本或观察值的分布,也有可能是精确计算的理论分布。 Q Q Q 代表一种理论,模型,描述或者对P的近似。尽管信息增益通常被直观地作为是一种度量或距离,但事实上信息增益并不是。就比如信息增益不是对称的,从 P P P 到 Q Q Q 的信息增益通常不等于从 Q Q Q 到 P P P 的信息增益。信息增益是f增益(f-divergences)的一种特殊情况。
I D 3 ID3 ID3 算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树,用计算出的信息增益最大的特征来建立决策树的当前节点。形式上,信息增益和互信息完全相同,但意义不一样,互信息是两个随机变量的地位相同。而信息增益,是把一个变量看成是减少另一个变量不确定度的手段。 g ( D , A ) = I ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=I(D,A)=H(D)-H(D|A) g(D,A)=I(D,A)=H(D)−H(D∣A)其中, D D D表示数据集, A A A 表示特征。信息增益表示得到特征 A A A 的信息而使得整体样本的不确定度下降的程度。在 I D 3 ID3 ID3 中,需要选择一个特征A使得信息增益最大,这样可以使得分类系统进行快速决策。
2.9信息增益率
在应用 I D 3 ID3 ID3 算法(信息增益)时,主要有四个主要的不足:一是不能处理连续特征;第二个就是用信息增益作为标准容易偏向于取值较多的特征;最后两个是缺失值处理的问和过拟合问题。在 C 4.5 C4.5 C4.5 算法中改进了上述4个问题。
C 4.5 C4.5 C4.5 主要用的是信息增益率,公式为: g r ( D , A ) = g ( D , A ) H ( A ) g_r(D,A)=\frac{g(D,A)}{H(A)} gr(D,A)=H(A)g(D,A)
2.10基尼系数
无论是 I D 3 ID3 ID3 还是 C 4.5 C4.5 C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。CART分类树算法使用基尼系数来代替信息增益率,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。具体的,在分类问题中,假设有 K K K个类别,第 k k k个类别的概率为 p k p_k pk, 则基尼系数的表达式为: G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\sum_{k=1}^{K}p_k(1-p_k)=1-\sum_{k=1}^{K}p_k^2 Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2 可以看出,基尼系数越小,表示选择该特征后熵下降最快,对分类模型效果更好,与信息增益、信息增益率的选择指标是相反的。基尼系数主要是度量数据划分对训练数据集D的不纯度大小,基尼系数越小,表明样本的纯度越高。其实为什么说基尼系数计算速度快呢,因为基尼系数实际上是信息熵的一阶进似,作用等价于信息熵,只不过是简化版本。根据泰勒级数公式,将 l n ( x ) ln(x) ln(x)在 x = 1 x=1 x=1处展开,忽略高阶无穷小,其可以等价为 l n ( x ) = x − 1 ln(x)=x-1 ln(x)=x−1,所以可以很容易得到上述定义。
对于个给定的样本 D D D,假设有 K K K个类别,第 k k k个类别的数量为 C k C_k Ck,则样本 D D D的基尼系数表达式为: G i n i ( D ) = 1 − ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 Gini(D)=1-\sum_{k=1}^{K}(\frac{|C_k|}{|D|})^2 Gini(D)=1−k=1∑K(∣D∣∣Ck∣)2 其中, ∣ D ∣ |D| ∣D∣表示样本个数。 ∣ C k ∣ |C_k| ∣Ck∣第 k k k个类别个数。
学习资料及引用
熵:宇宙的终极规则
机器学习各种熵:从入门到全面掌握
信息熵是什么?
信息熵的前世今生
互信息公式及概述
决策树算法原理