图像的梯度

Sobel算子

sobel算子需要应用两个矩阵进行计算，分别为：

我们需要用这样的矩阵与图像中每一个3×3区域做按位相乘再相加的操作。很显然，sobel算子是考虑某个3×3矩阵的第一列与第三列（或第一行与第三行）的一种算术关系，如：

最后的运算结果如果小于0，则会被截断为0，如果大于255，则会保留为255。
使用sobel算子处理图像需要使用的函数是Sobel(src, ddepth, dx, dy, ksize)，其中：

• ddepth:表示图像的深度（像素矩阵中元素的数据类型）
• dx和dy分别表示水平和竖直方向
• ksize是Sobel算子的大小（维度）

import cv2
import numpy as np
img = cv2.imread('pie.png')
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3) # 水平方向梯度
cv2.imshow('sobelx', sobelx)
cv2.waitKey(0)
cv2.destroyAllWindows()

从结果来看，我们并没有获得很好的水平梯度，因为右半面没有边缘信息。这就是因为使用sobel算子，小于0的点会被截断为0。因此，我们需要一个绝对值函数，用以复原又半圆的边缘信息：

import cv2
import numpy as np
img = cv2.imread('pie.png')
# 如果需要获取竖直梯度，可以将第三、四个参数改为0,1
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
# 将sobelx矩阵取绝对值
sobelx = cv2.convertScaleAbs(sobelx)

cv2.imshow('sobelx',sobelx)
cv2.waitKey(0)
cv2.destroyAllWindows()

这样就可以了。如果我们需要在一张图片上显示水平和竖直梯度的图像，可以借助之前讲到过的addWeighted()函数：

import cv2
import numpy as np
img = cv2.imread('pie.png')
# dx=1，dy=0
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
# 将sobelx矩阵取绝对值
sobelx = cv2.convertScaleAbs(sobelx)
# dx=0，dy=1
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
# 将sobely矩阵取绝对值
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx,0.5,sobely,0.5,0)
cv2.imshow('sobelxy',sobelxy)
cv2.waitKey(0)
cv2.destroyAllWindows()

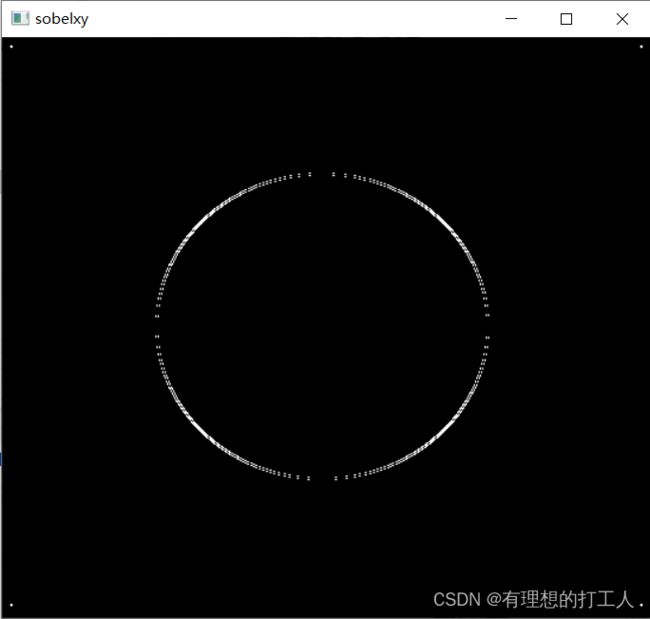
可能有小伙伴会问，可不可以将dx和dy都设置成1，得到这个结果呢？但事实上，这样的方法不能很好地获得梯度图像：

import cv2
import numpy as np
img = cv2.imread('pie.png')
sobelxy = cv2.Sobel(img,cv2.CV_64F,1,1,ksize=3)
sobelxy = cv2.convertScaleAbs(sobelxy)
cv2.imshow('sobelxy',sobelxy)
cv2.waitKey(0)
cv2.destroyAllWindows()

所以，我们最好还是采用分别求出后再相加的方式获取边缘信息。

Scharr算子

scharr算子和sobel算子很像，它应用的两个矩阵为：

对应的参数为：Scharr(src, ddepth, dx, dy, ksize)，其中的参数含义与Sobel函数一致。该函数的特点在于会把差异方的更大，可以得到更丰富的边缘信息。这里先不给大家展示，后面再做对比。

laplacian算子

拉普拉斯算子和前面两种有所不同，他只应用一个矩阵：

从形式上看，拉普拉斯算子更注重中心位置的值，因此这种方法对噪点的处理结果应该较差。下面我们来将这三种算子应用到图像处理之中看看结果：

三种算子结果比较

import cv2
import numpy as np
import matplotlib.pyplot as plt
#不同算子的差异
img = cv2.imread('lena.jpg',cv2.IMREAD_GRAYSCALE) # 读取灰度图
# sobel算子
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.convertScaleAbs(sobely)
sobelxy =  cv2.addWeighted(sobelx,0.5,sobely,0.5,0)
# scharr算子
scharrx = cv2.Scharr(img,cv2.CV_64F,1,0)
scharry = cv2.Scharr(img,cv2.CV_64F,0,1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
scharrxy =  cv2.addWeighted(scharrx,0.5,scharry,0.5,0)
# laplacian算子
laplacian = cv2.Laplacian(img,cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)

titles=['sobel','scharr','laplacian']
img_show=[sobelxy,scharrxy,laplacian]
fig, ax = plt.subplots(1,3)
for i in range(3):
    ax[i].set_title(titles[i])
    ax[i].imshow(cv2.cvtColor(img_show[i], cv2.IMREAD_GRAYSCALE))
    ax[i].axis('off')
plt.show()

从结果中也可以看出，Scharr和sobel算子都能够获取边缘信息，但Scharr算子可以捕捉到更丰富的梯度信息。拉普拉斯算子效果不是很理想，因此不建议单独使用。

Canny边缘检测

.canny边缘检测是一整套完整的理论，只想看代码的小伙伴可以直接画到最后~
canny边缘检测主要有以下的几个步骤：

• 1. 使用高斯滤波器，以平滑图像，滤除噪声。
• 2. 计算图像中每个像素点的梯度强度和方向。
• 3. 应用非极大值（Non-Maximum Suppression）抑制，以消除边缘检测带来的杂散响应。
• 4. 应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘。
• 5. 通过抑制孤立的弱边缘最终完成边缘检测。

高斯滤波器

高斯滤波消除噪声的原理我们已经讲过，但是这里还需要对H矩阵进行一下归一化处理（H矩阵所有值之和为1）：

梯度和方向

在这个环节，我们需要得到梯度的大小和方向，也就需要知道x方向的梯度和y方向的梯度，获得方法如下：

非极大值抑制

如果我们手里有一个存储了每个像素点梯度值的矩阵，那么我们就需要判断没一个像素点是不是该梯度方向上的极大值。由极大值的定义可以知道，只要满足该梯度值比对应方向上的最近两个（位于该点上下或左右）的值大即可。我们假设像素点是真正意义上的点，而不是一个小正方形，如：

实际上这幅图中我们假设g1,g2,g3,g4以及c是相邻的像素点，即他们有以下的位置关系：

其中θ是c点的梯度方向，则有一条斜率为(180°-θ)的过c的直线会交g1，g2连线上的一点（设为m），交g3，g4连线上的一点（设为n），我们只需要保证c比m和n的值都要大，就可以说c是一个极大值。但是m和n并不是具体值，该怎么办呢？我们需要用线性差值法给m和n赋予一个值。
所谓线性插值，即：

其中，|g₁m|为g₁点到m位置的距离，且|g₁m|+|g₂m|=1，n的计算方法也是同理。如果c同时大于m和n，那么将予以保留，否则，要对c进行抑制。
为了简化计算，由于一个像素周围有八个像素，我们可以简化成八个方向：

如果θ不等于这八个方向之一，我们会就近分配一个方向作为θ，这样就不需要插值了。

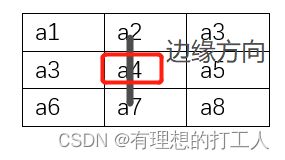
以a4为例，假如a4的梯度方向是0（水平方向），那么就需要考虑a4和a5以及a3的大小，如果a4是这三个数中的最大值，既可以认为a4是个会被保留的极大值，由于边缘的方向垂直于梯度方向，所以在a4附近的边缘是垂直方向的：

双阈值检测

上文我们已经介绍了非极大值抑制，但是保留下来的值也不能全部认定为边缘信息，双阈值检测就是确定图像边缘的又一个重要指标：

我们需要设置最大值和最小值，如果保留下来的梯度大于maxVal，我们认为这是一个边界点，如果小于minVal，这个梯度值便不是边缘，将会被抑制。假如梯度介于这两者之间，那就需要考虑这个值是否临接边界。如上图所示，假如A,C,B是三个梯度，而这三个梯度值的位置关系为：

因为C与A临接，所以C也是图像边缘，而B不与边缘值临接，所以B不是边缘。

代码

canny算法虽然理论复杂，但写起来非常简单，依赖的函数是：

cv2.Canny(img,minVal,maxVal)

img是一个灰度图矩阵，minVal和maxValue是双阈值检测中的设置的最小值和最大值：

import cv2
import numpy as np

img=cv2.imread("lena.jpg",cv2.IMREAD_GRAYSCALE)
v1=cv2.Canny(img,80,150)
v2=cv2.Canny(img,50,100)

res = np.hstack((v1,v2))
cv2.imshow('res',res)
cv2.waitKey(0)
cv2.destroyAllWindows()

可以发现，把minVal或maxVal设置的越大，保留下来的边缘信息就越少，相对也会精确一些，反之保留的边缘信息会更多更完整，但是也会有一些噪点会被保留下来。小伙伴们自己换一些图片试试提取图片边缘吧~