利用随机森林对特征重要性进行评估(公式原理)
本文参考来源于:
杨凯, 侯艳, 李康. 随机森林变量重要性评分及其研究进展[J]. 2015.
码字不易,各位看官大大的赞是我更细的动力!
一、引言
随机森林( r a n d o m f o r e s t , R F random\;\; forest,RF randomforest,RF)由 B r e i m a n Breiman Breiman等人在2001年提出。
R F RF RF具有很高的预测准确率,对异常值和噪声有很强的容忍度,能够处理高维数据(变量个数远大于观测个数),有效地分析非线性、具有共线性和交互作用的数据, 并能够在分析数据的同时给出变量重要性评分( v a r i a b l e i m p o r t a n c e m e a s u r e s , V I M variableimportance\;\;measures,VIM variableimportancemeasures,VIM)。这些特点使得 R F RF RF特别适用于高维组学数据的研究,即在对疾病进行分类的同时通过 V I M VIM VIM值筛选出潜在的生物标志物,研究疾病发生、发展的生物学机制。然而, 由于在实际中由RF筛选变量使用的统计量不同,可能会使结果有较大的差异,为此本文在简单介绍 R F RF RF筛选变量的基础上,拟针对目前随机森林变量重要性评分的不同计算方法和新近提出的改进方法, 说明其在高维组学数据分析中的应用。
二、随机森林的基本原理
了解决策树的算法,那么随机森林是相当容易理解的。随机森林的算法可以用如下几个步骤概括:
1.用有抽样放回的方法(bootstrap)从样本集中选取 n n n个样本作为一个训练集;
2.用抽样得到的样本集生成一棵决策树。在生成的每一个结点:
(1)随机不重复地选择 d d d个特征
(2)利用这 d d d个特征分别对样本集进行划分,找到最佳的划分特征(可用基尼系数、增益率或者信息增益判别)
3.重复步骤1到步骤2共 k k k次, k k k即为随机森林中决策树的个数。
4.用训练得到的随机森林对测试样本进行预测,并用投票法决定预测的结果。
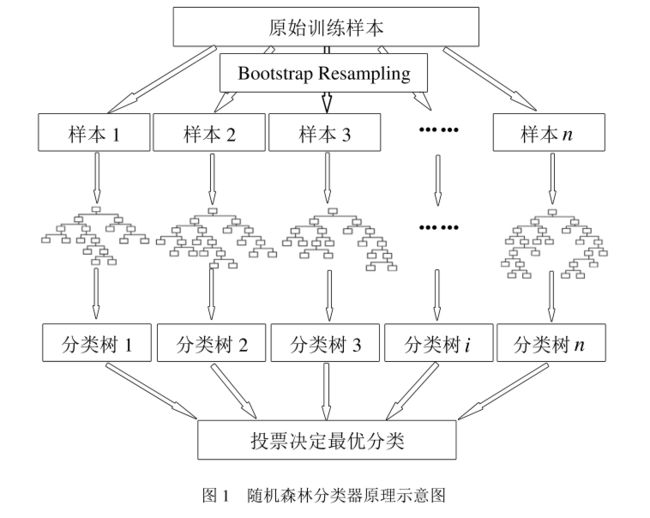
下图比较直观地展示了随机森林算法:
图片来源:
杨凯, 侯艳, 李康. 随机森林变量重要性评分及其研究进展[J]. 2015.
R F RF RF中的每一棵分类树为二叉树,根节点包含全部训练自助样本,按照一定的原则,在每个节点从一组随机选取的变量中选择使分枝后节点“不纯度” 最小的变量作为分枝变量,分裂为左节点和右节点, 它们分别包含训练数据的一个子集, 分裂后的节点按照同样规则继续分裂, 直到满足分枝停止规则而停止生长, 具体过程见图 1。
“不纯度” 的衡量标准包括 G i n i Gini Gini不纯度、 熵和错误率等。 变量筛选使用 V I M VIM VIM统计量。
三、随机森林常规的变量重要性评分
现假定有变量 X 1 , X 2 , L , X M X_1\;,\;X_2\;,\;L\;,\;X_M X1,X2,L,XM,需要计算出 M M M个 V I M VIM VIM得分统计量。
R F RF RF常规的 V I M VIM VIM计算方法分为两种,即根据 G i n i Gini Gini指数和袋外数据( O O B OOB OOB) 错误率计算得到, 变量 X j X_j Xj的得分统计量分别用 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)和 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)表示。
2.1 Gini指数
统计量 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)表示第 j j j个变量在 R F RF RF所有树中节点分裂不纯度的平均改变量。 G i n i Gini Gini指数的计算公式为:
G I m = ∑ k = 1 K p ^ m k ( 1 − p ^ m k ) ( 1 ) GI_{m}=\sum_{k=1}^K\hat{p}_{mk}(1-\hat{p}_{mk})\;\;\;\;(1) GIm=k=1∑Kp^mk(1−p^mk)(1)
K K K为自助样本集的类别数, p ^ m k \hat{p}_{mk} p^mk为节点 m m m样本属于第 k k k类的概率估计值,当样本为二分类数据时( K = 2 K=2 K=2) ,节点 m m m的 G i n i Gini Gini指数为:
G I m = 2 p ^ m ( 1 − p ^ m ) ( 2 ) GI_{m}=2\hat{p}_{m}(1-\hat{p}_{m})\;\;\;\;(2) GIm=2p^m(1−p^m)(2)
p ^ m \hat{p}_{m} p^m为样本在节点 m m m属于任意一类的概率估计值。
变量 X j X_j Xj在节点 m m m的重要性,即节点 m m m分枝前后 G i n i Gini Gini指数变化量为:
V I M j m ( G i n i ) = G I m − G I l − G I r ( 3 ) VIM_{jm}^{(Gini)}=GI_{m}-GI_{l}-GI_{r}\;\;\;\;(3) VIMjm(Gini)=GIm−GIl−GIr(3)
G I l GI_{l} GIl和 G I r GI_{r} GIr分别表示由节点 m m m分裂的两新节点的 G i n i Gini Gini指数。
如果变量 X j X_j Xj在第 i i i棵树中出现 M M M次,则变量 X j X_j Xj在第 i i i棵树的重要性为:
V I M i j ( G i n i ) = ∑ m = 1 M V I M j m ( G i n i ) ( 4 ) VIM_{ij}^{(Gini)}=\sum_{m=1}^MVIM_{jm}^{(Gini)}\;\;\;\;(4) VIMij(Gini)=m=1∑MVIMjm(Gini)(4)
变量 X j X_j Xj在 R F RF RF中的 G i n i Gini Gini重要性定义为:
V I M j ( G i n i ) = 1 n ∑ i = 1 n V I M i j ( G i n i ) ( 5 ) VIM_{j}^{(Gini)}=\frac{1}{n}\sum_{i=1}^nVIM_{ij}^{(Gini)}\;\;\;\;(5) VIMj(Gini)=n1i=1∑nVIMij(Gini)(5)
其中, n n n为 R F RF RF中分类树的数量。
2.2 OOB 错误率
V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)的定义为:在 R F RF RF的每棵树中,使用随机抽取的训练自助样本建树,并计算袋外数据( O O B OOB OOB)的预测错误率,然后随机置换变量 X j X_j Xj的观测值后再次建树并计算 O O B OOB OOB的预测错误率,最后计算两次 O O B OOB OOB错误率的差值经过标准化处理后在所有树中的平均值即为变量 X j X_j Xj的置换重要性( V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB))。
变量 X j X_j Xj在第 i i i棵树的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)为:
V I M j ( O O B ) = ∑ p = 1 n o i I ( Y p = Y p i ) n o i − ∑ p = 1 n o i I ( Y p = Y p , π j i ) n o i VIM_{j}^{(OOB)}=\frac{\sum_{p=1}^{n_o^i}I(Y_p=Y_p^i)}{n_o^i}-\frac{\sum_{p=1}^{n_o^i}I(Y_p=Y_{p,\pi_j}^i)}{n_o^i} VIMj(OOB)=noi∑p=1noiI(Yp=Ypi)−noi∑p=1noiI(Yp=Yp,πji)
其中, n o i n_o^i noi为第 i i i棵树 O O B OOB OOB数据的观测例数, I ( g ) I(g) I(g)为指示函数,即两值相等时取1,不等时取0; Y p ∈ { 0 , 1 } Y_p\in\{0,1\} Yp∈{0,1}为第 p p p个观测的真实结果, Y p i ∈ { 0 , 1 } Y_p^i\in\{0,1\} Ypi∈{0,1}为随机置换前第 i i i棵树对 O O B OOB OOB数据第 p p p个观测的预测结果, Y p , π j i ∈ { 0 , 1 } Y_{p,\pi_j}^i\in\{0,1\} Yp,πji∈{0,1}为随机置换后第 i i i棵树对 O O B OOB OOB数据第 p p p个观测的预测结果。
当变量 j j j没有在第 i i i棵树中出现时, V I M i j ( O O B ) = 0 VIM_{ij}^{(OOB)}=0 VIMij(OOB)=0
变量 X j X_j Xj在 R F RF RF中的置换重要性定义为:
V I M j ( O O B ) = ∑ i = 1 n V I M i j ( O O B ) n VIM_{j}^{(OOB)}=\frac{\sum_{i=1}^nVIM_{ij}^{(OOB)}}{n} VIMj(OOB)=n∑i=1nVIMij(OOB)
其中, n n n为 R F RF RF中分类树的数量。
2.3 常规变量重要性评分的优缺点
V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)在数据挖掘中估计变量重要性时有着广泛的应用。 当变量为连续型变量且互不相关时, V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)的估计是无偏的;
当信噪比较低时, V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)的准确性也高于 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB),因此, V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)有更高的稳定性。
然而, 当同时存在连续变量和分类变量或者分类变量的水平数不同时, V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)估计则不够准确。由于 K K K个水平的分类变量在节点处可以有 2 K − 1 − 1 2^{K-1}-1 2K−1−1种分割, 连续变量在节点处可以有 b − 1 b-1 b−1种分割( b b b为样本量)。在备选分割较多时, 即使变量没有分类作用, 也可能使 G i n i Gini Gini指数降低, 从而更容易被选为分枝变量, 即 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)被高估。 实际上, 由于 G i n i Gini Gini指数的计算问题, 水平数多的分类变量的 G i n i Gini Gini指数降低会大于水平数少的分类变量。
当分类变量水平数相同时, 如果不同变量的水平间差别不同, 容易过高估计水平间差别大的变量的 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini) 。 在 SNP 数据分析中, Nicodemus 等人指出当所有 SNP 都不具有分类能力时,不相关 SNP 的 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)高于高度相关 SNP 的 V I M j ( G i n i ) VIM_{j}^{(Gini)} VIMj(Gini)
事实上, V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)在实际中的应用范围更加广泛。 由于 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)是通过 O O B OOB OOB数据计算的, 因此可以看作变量具有的分类能力, 没有分类能力的变量在观测值置换前后的 O O B OOB OOB错误率不会发生改变, 即数学期望 E ( V I M j ( O O B ) ) = 0 E(VIM_{j}^{(OOB)})=0 E(VIMj(OOB))=0,此外, V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)不仅能够衡量变量单独的分类能力, 还能够衡量变量间交互作用的分类能力。
当同时存在连续变量和分类变量或者分类变量水平数不同时, 并不会影响 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)准确性。 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)是通过随机置换变量观测值前后 O O B OOB OOB错误率的差值计算的, 即使没有分类作用, 水平数多的变量也更容易被选为分枝变量, 但置换前后并不会影响 O O B OOB OOB错误率,同时会使 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)的变异增大。
在分类数据不平衡时, V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)的准确性会受到一定影响。例如多数为正常人, 无论变量是否置换, 大部分的数据都会被预测为正常, 虽然 O O B OOB OOB错误率受到的影响可能不大,但却会严重低估所有变量的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)。
当单棵树的预测准确率较低时(如 O O B OOB OOB错误率达到 50%) , 会低估变量的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)
当置换前 O O B OOB OOB错误率已经很大时, 置换变量观测值使得 OOB 错误率变大的可能性降低, 从而低估变量的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)
当没有分类能力的变量与有分类能力的变量相关时, 可能低估相关有分类能力变量的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB),且估计方差变异增加, 而此时没有分类能力变量的 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)则被高估。
组学数据中存在大量的噪声变量, 当变量数目巨大而具有分类能力的变量所占比例很小时, R F RF RF建模容易受到大量噪声变量的干扰, 使变量的 V I M VIM VIM计算受到影响, 变量筛选的结果不可信。
2.4 变量重要性( VIM ) 的显著性检验
V I M VIM VIM给出了变量的重要性排序, 但无法在变量筛选时给出显著性假设检验的阈值。 事实上, 当所有变量都没有分类能力时, V I M VIM VIM也会给出变量重要性排序, 筛选出不具有分类能力的变量; 而当有分类能力的变量很多时, 仅通过变量的排序进行变量筛选, 可能漏掉一些具有分类能力的变量。
B r e i m a n Breiman Breiman等人提出通过 Z Z Z值直接计算 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)的显著性, 即:
Z = V I M j ( O O B ) / ( σ ^ / n ) Z=VIM_{j}^{(OOB)}/(\hat{\sigma}/\sqrt{n}) Z=VIMj(OOB)/(σ^/n)
其中, σ ^ \hat{\sigma} σ^为 R F RF RF中各棵树 V I M j ( O O B ) VIM_{j}^{(OOB)} VIMj(OOB)的标准差, n n n为随机森林( R F RF RF)中树的数量。 然而, S t r o b l Strobl Strobl等人通过模拟实验表明: Z Z Z值的检验效能与样本量 b b b及树的数量 n n n有很大的关系, 当样本量 b b b很大而树的数量 n n n小时, 检验效能接近于0。