论文阅读:Privacy Leakage of Real-World Vertical Federated Learning
文章目录
- 联邦学习
-
-
- 横向联邦学习
- 纵向联邦学习
- 小节
-
- 反向攻击
-
-
- 1、加噪声破坏神经网络
- 2、成员推理攻击
- 同态加密
- Secure XGBoost
- 现实世界中联邦学习的隐私泄露
- 反向乘法攻击
- 反向求和攻击
-
- 幻数
-
- 一些可能的防御措施
联邦学习
为什么叫联邦学习? 联邦学习的概念是在2016年由McMahan等人在2016年引入:“我们之所以将我们的方法称为联邦学习,因为学习任务是通过由中央服务器协调的参与设备(我们称为客户端)的松散联邦来解决的。
联邦学习(Federated Learning, a.k.a. Federated Machine Learning)可以分为三类:横向联邦学习(Horizontal Federated Learning),纵向联邦学习(Vertical Federated Learning),联邦迁移学习(Federated Transfer Learning)。
有不少读者说,横向联邦学习和纵向联邦学习容易混淆,不太清楚为什么这么分类。我在这里再解释一下横向联邦学习和纵向联邦学习。
横向联邦学习
数据矩阵(也可以是表格,例如,Excel表格)的横向的一行表示一条训练样本,纵向的一列表示一个数据特征(或者标签)。通常用表格查看数据(例如,病例数据),用一行表示一条训练样本比较好,因为可能有很多条数据。
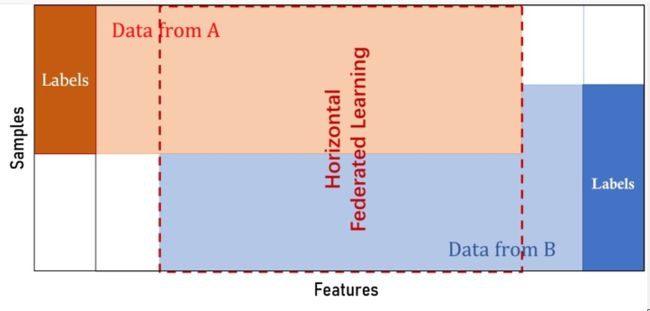
横向联邦学习,适用于参与者的数据特征重叠较多,而样本ID重叠较少的情况,例如,两家不同地区的银行的客户数据。“横向”二字来源于数据的“横向划分(horizontal partitioning, a.k.a. sharding)”。如图1所示例,联合多个参与者的具有相同特征的多行样本进行联邦学习,即各个参与者的训练数据是横向划分的,称为横向联邦学习。图2给出了一个横向划分表格的示例。横向联邦使训练样本的总数量增加。
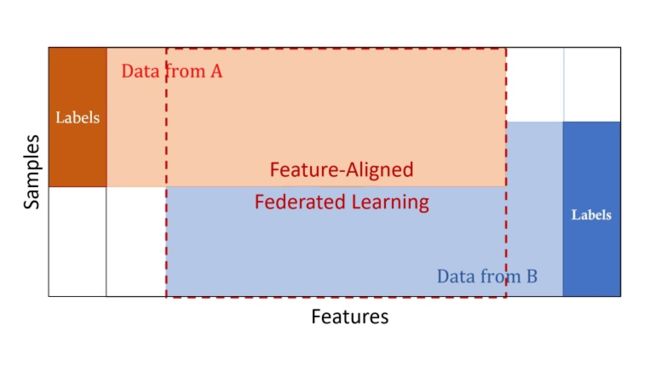
横向联邦学习也称为特征对齐的联邦学习(Feature-Aligned Federated Learning),即横向联邦学习的参与者的数据特征是对齐的,如图3所示例。“特征对齐的联邦学习”这个名字有点长,还是用“横向联邦学习”比较好,也称为特征对齐的联邦学习,横向联邦使训练样本量增大。
纵向联邦学习
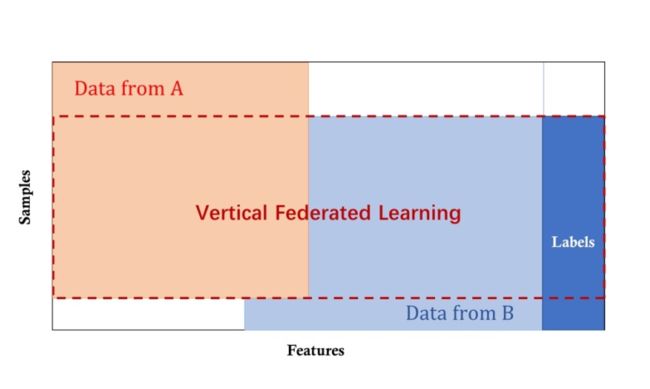
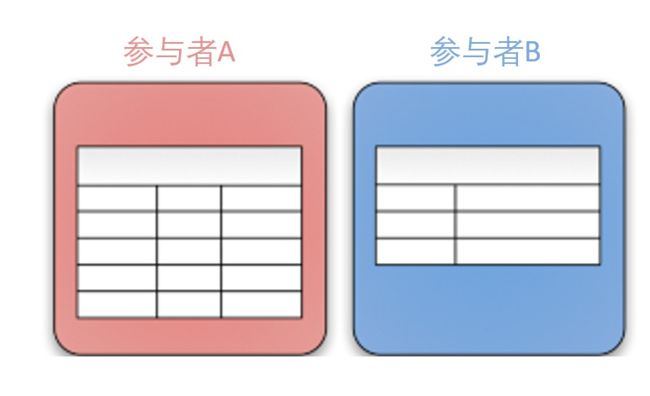
纵向联邦学习,适用于参与者训练样本ID重叠较多,而数据特征重叠较少的情况,例如,同一地区的银行和电商的共同的客户数据 [1, 2]。“纵向”二字来源于数据的“纵向划分(vertical partitioning)”。如图4所示例,联合多个参与者的共同样本的不同数据特征进行联邦学习,即各个参与者的训练数据是纵向划分的,称为纵向联邦学习。图5给出了一个纵向划分表格的示例。纵向联邦学习需要先做样本对齐,即找出参与者拥有的共同的样本,也就叫“数据库撞库(entity resolution, a.k.a. entity alignment)”。只有联合多个参与者的共同样本的不同特征进行纵向联邦学习,才有意义。纵向联邦使训练样本的特征维度增多。
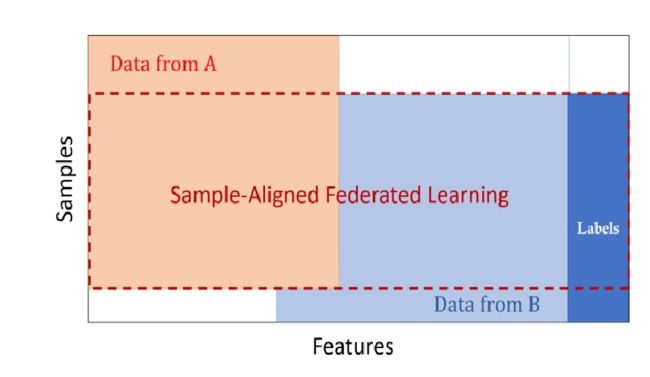
纵向联邦学习也称为样本对齐的联邦学习(Sample-Aligned Federated Learning),即纵向联邦学习的参与者的训练样本是对齐的,如图6所示例。“样本对齐的联邦学习”这个名字有点长,还是用“纵向联邦学习”比较好,纵向联邦使训练数据特征维度增加。
小节
横向联邦学习的名称来源于训练数据的“横向划分”,也就是数据矩阵或者表格的按行(横向)划分。不同行的数据有相同的数据特征,即数据特征是对齐的。
纵向联邦学习的名称来源于训练数据的“纵向划分”,也就是数据矩阵或者表格的按列(纵向)划分。不同列的数据有相同的样本ID,即训练样本是对齐的。
反向攻击
1、加噪声破坏神经网络

我们可以写个反向攻击的代码,作为检验。

代码附在了本文的附注。
2、成员推理攻击
成员推理攻击是用来判断某个样本是否属于目标模型的训练数据集,从而得知该样本的一些集体属性。比如说,某医院根据一批患者的症状训练了一个机器模型,并且把这个模型公开给了大家用;而我手里有某个人的生理特征,那么我可以利用成员推理攻击来推测这个人的数据是否被用于训练医院发布的模型,从而知道他是否去医药看过这个病。
一种比较经典的成员推理攻击是这样的:被攻击的目标是一批隐私训练数据集和利用这批训练集训练出来的模型。攻击者会通过白盒窃取或者黑盒探测的方式得到和目标模型的结构、参数都相似的影子模型,然后生成和目标数据集分布相似的仿真数据集,最后用影子模型和仿真数据集训练一个分类模型,这个分类模型可以根据某样本经过目标模型的输出来判断它是否属于目标训练数据集。当然,在真实场景中,影子模型和仿真数据集的逼真程度都不是很高,所以成员推理攻击大多时候是作为一个测试方法,评估模型训练过程的隐私泄露程度。
还有其他多样的攻击模式,在此不作赘述。
同态加密
同态加密是基于数学难题的计算复杂性理论的密码学技术。对经过同态加密的数据进行处理得到一个输出,将这一输出进行解密,其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。
很多众所周知的公钥加密方案其实都具有同态的性质,只是它们都只支持部分同态,也就是说它们只支持在密文上进行加法或乘法操作,但不能既做加法又做乘法。比如著名的RSA加密方案,支持的就是同态乘法:
[ x ] ≔ x e [x]≔x^e [x]:=xe
[ x ] ⋅ [ y ] = ( x y ) e [x]⋅[y]=(xy)^e [x]⋅[y]=(xy)e
还有1999年出现的著名的Paillier加密方案支持的就是加法同态:
[ x ] ≔ g x r n [x]≔g^x r^n [x]:=gxrn
[ x ] ⋅ [ y ] = g x + y ( r x r y ) n [x]⋅[y]=g^{x+y }(r_x r_y )^n [x]⋅[y]=gx+y(rxry)n
Secure XGBoost
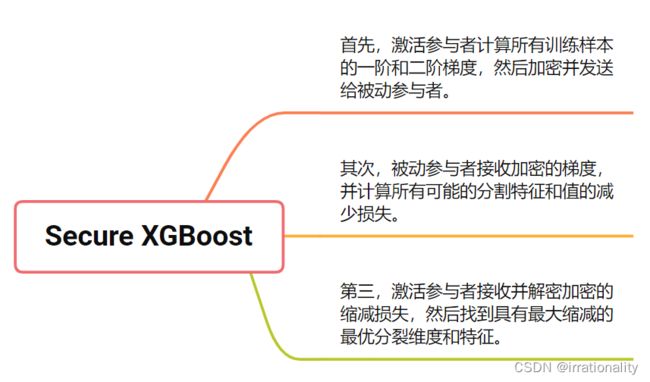

Secure XGBoost的原理很简单,用分裂之后的分数减去未分裂的分数(和信息增益的概念差不多),这个分数的计算也是和一阶导数和二阶导数有关的。

现实世界中联邦学习的隐私泄露
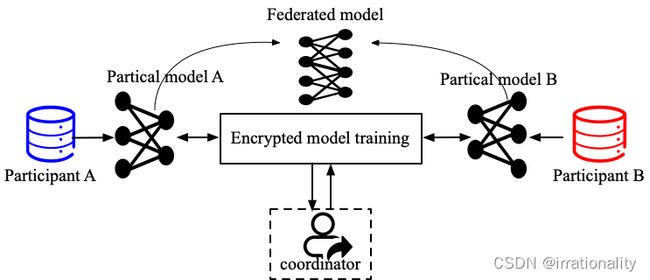
完整的数据集X被垂直分割为参与者A和参与者B分别持有的 X A X_A XA和 X B X_B XB。然后,A和B局部维护部分模型,并交换加密的部分梯度和其他基本信息,以在完整数据集X上学习联合模型。
反向乘法攻击
- 步骤1.敌方在每个小批量的协作训练期间秘密存储中间加密乘法结果。具体而言,对于每个小批量S,敌方秘密存储(i)B的部分数据和系数 [ [ 1 4 θ t B X S B ] ] [\![\frac{1}{4} {\boldsymbol{\theta}}_{t}^{\mathcal{B}}\mathbf{X}_{S}^{\mathcal{B}}]\!] [[41θtBXSB]]之间的乘法结果,以及(ii)梯度的系数更新, g t B g_{t}^{\mathcal{B}} gtB。
请注意,此加密信息是从B发送的,用于联合计算小批量上的加密梯度。 - 步骤2.对手解密每个小批量计算的 [ [ 1 4 θ t B X S B ] ] [\![\frac{1}{4} {\boldsymbol{\theta}}_{t}^{\mathcal{B}}\mathbf{X}_{S}^{\mathcal{B}}]\!] [[41θtBXSB]]。请注意,A和B使用相同的公钥进行加密,C使用相应的私钥进行解密。因此,对手可以使用C的私钥解密密文。
- 步骤3.对手反转乘法项以获得B的训练数据。对于一个特定的小批量 X S B \mathbf{X}_{S}^{\mathcal{B}} XSB,对手在两个连续的训练周期上具有以下等式: 1 4 θ t B X S B − 1 4 θ t − 1 B X S B = g t B X S B \frac{1}{4} {\boldsymbol{\theta}}_{t}^{\mathcal{B}}\mathbf{X}_{S}^{\mathcal{B}} - \frac{1}{4} {\boldsymbol{\theta}}_{t-1}^{\mathcal{B}}\mathbf{X}_{S}^{\mathcal{B}} =g_{t}^{\text{B}}\mathbf{X}_{S}^{\mathcal{B}} 41θtBXSB−41θt−1BXSB=gtBXSB,其中只有 X S B \mathbf{X}_{S}^{\mathcal{B}} XSB 是未知参数。如果对手得到足够的方程,他可以计算出未知的 X S B \mathbf{X}_{S}^\mathcal{B} XSB 。对手至少需要 ∣ B ∣ |\mathcal{B}| ∣B∣个方程来求解未知参数,其中 ∣ B ∣ |\mathcal{B}| ∣B∣表示B的私有数据中的特征数。
反向求和攻击
我们设计了一种针对SecureBoost的反向和攻击。在我们的攻击中,我们假设对手完全控制参与者 A \mathcal{A} A。下面列出了我们攻击的两个主要步骤。
- 步骤1.敌方控制 A \mathcal{A} A将幻数 编码为一阶和二阶梯度的密文。这里,术语幻数指的是不太可能被误认为其他含义的独特值(即全局唯一标识符)。
- 步骤2. 敌方存储从 B \mathcal{B} B接收的第一和第二梯度和。然后,对手利用编码的幻数反向设计梯度和中的所有加法项。这些反向项揭示了 B \mathcal{B} B 的训练数据的偏序。
幻数
上面提到的幻数,我们在第一和第二梯度的密文中对幻数进行编码。实际上,公共加密生态系统对 1024 1024 1024-位数字进行加密。对于梯度的 64 64 64位浮点数,生态系统通常将其填充 960 960 960零,以获得用于加密的 1024 1024 1024位数字。 960 960 960零不会降低浮点数精度,因为它们被填充在最低有效位置。在我们的攻击中,我们没有填充960个零,而是设计将 64 64 64位数字填充为 960 960 960位的幻数。
幻数是攻击者用来识别用该幻数编码的特定梯度值的唯一标识符。为此,我们设计了这样一种生成模式,可以生成尽可能多的幻数来识别训练数据的梯度。图[4]显示了我们的幻数的架构。
如图[4]所示,幻数有两部分:组标识符和随机值。组标识符是 n n n基位置数字系统下的一个热向量,用于标识编码示例所属的特定组示例。例如,在base-10系统中,“ 0 ⋯ 01 0\cdots01 0⋯01”表示该示例属于组 1 1 1。随机值用于表示来自同一组的不同示例。使用组标识符和随机值,来自同一组的示例具有相同的组标识符,而不同的随机值。
下面,我们给出了一个使用基数为 16 16 16的位置数字系统生成组标识符的示例。为简单起见,我们仅使用960位中的20位来编码该幻数。我们将前4位设置为随机值位,并将剩余的 16 16 16位设置为组标识符位,以识别最多4个( = log 16 2 6 =\log_{16}{{2}^{6}} =log1626)唯一的示例组。给定60美元的数据样本,我们首先将它们分成4美元的组,每个组有60/4美元的样本。第1至第15个样品被置于第一组,第16至第30个样品被放入第二组,第31至第45个样品被放置在第三组,第46至第60个样品被放在第四组。对于第一组中的数据样本,我们生成前4位作为随机值,其余16美元位的组标识符为“0X0001”。类似地,对于第二组中的数据样本,幻数的前4位是随机值,组标识符为“0X0010”。

在此示例中,我们利用 20 20 20 的 960 960 960 位对幻数进行编码,将前 4 4 4 位设置为随机值位,并将位置数值系统的基数设置为 4 4 4。我们假设一个包含五个样本的数据箱 B B B: x 2 \mathbf{x}_{2} x2, x 17 \mathbf{x}_{17} x17, x 517 \mathbf{x}_{517} x517, x 520 \mathbf{x}_{520} x520, x 2400 \mathbf{x}_{2400} x2400,其中仅选择 x 2 \mathbf{x}_{2} x2 和 x 17 \mathbf{x}_{17} x17 来编码幻数。 x 2 \mathbf{x}_{2} x2 的幻数是 ‘0X30001’,而 x 14 \mathbf{x}_{14} x14 的幻数是 ‘0X20010’。在此示例中, G B G_B GB 的幻数总和为“0X50011”(=“0X30001” + “0X20010”)。一旦提取“0X50011”的神奇和,对手就可以知道 B B B必须包含一个来自组 1 1 1的样本和一个来自组 2 2 2的样本。通过两个幻数的随机值之和为“0X5”的附加信息,对手可以很容易地找出 x 2 \mathbf{x}_{2} x2和 x 17 \mathbf{x}_{17} x17在 B B B。
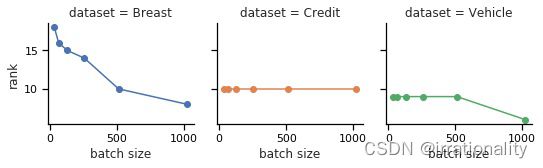
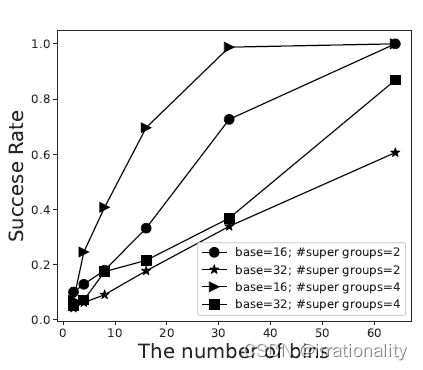
Bin 文件大小的影响 接下来,我们将探讨 Bin 大小对攻击成功率的影响。在这个实验中,我们设置了两个参与者共同学习 D 1 D_1 D1上的XGBoost模型。图 [6] 显示了目标参与者将训练数据拆分为不同数量的箱时的攻击成功率。
如图所示,攻击成功率随着目标训练数据上数据箱数量的增加而增加。这背后的原因很简单。大量数据条柱会导致单个条柱中的样本减少,从而使对手更容易准确地计算出此条柱的梯度和的所有加法项。我们还可以从图中观察到,少量(接近30)的数据箱会导致0.5以上的攻击成功率。
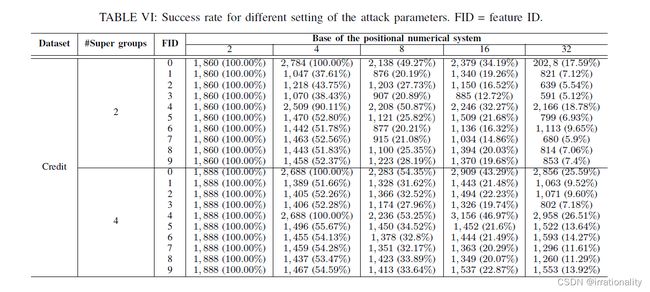
攻击参数的影响最后,我们证明了两个攻击参数,位置数值系统的基数和超群的数量,与破解偏序的大小高度相关,因为它们决定了可以用幻数编码的最大样本数。在此实验中,我们使用两个攻击参数的不同设置对信用数据集运行攻击。
下表显示了通过不同的数值基础和超群大小,攻击的成功率以及成功破解的样本数。如表所示,使用较小的基数和组大小会导致最高的攻击成功率,而使用较大的基数和组大小会导致更多的破解样本。这背后的原因是双重的。通过使用较大的基数和超群大小,编码样本的容量增加,这导致对手在更多样本中编码幻数,因此对手可以获得有关梯度和的加法项的更多信息。然而,大容量也会导致来自同一组的样本搜索空间很大,这使得对手更难找出所有正确的加法项。
一些可能的防御措施
训练前的参数设置。
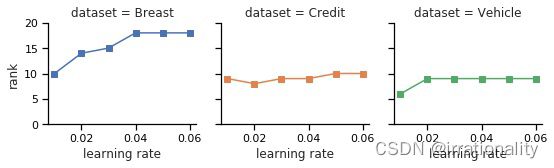
(i)如果batchsize较小,反向乘法攻击可以准确地推断出目标参与者的所有私有数据;
(ii)如果我们提高学习率,攻击性能可以大大提高。
这些观察结果激励我们选择大批量和小学习速率来缓解反向乘法攻击。但是,大批量需要大网络带宽供两个参与者进行通信,而小批量学习大大增加了训练时间。考虑到时间和经济成本,这不是一个有希望广泛运用的防御措施。
隐藏部分信息。
SecureBoost的一种可能的防御方法是使用秘密共享来隐藏部分信息。也就是说,为所有节点引入一个指示向量来记录哪些样本属于它们,并将指示向量转换为秘密共享变量以进一步保护隐私。通过这种方式,单个节点中样本的导数之和可以计算为指标向量和导数向量的内积。虽然这种方法
可以保护参与者部分订单的隐私,但它可能无法抵御我们的反向求和攻击。在反向求和攻击中,对手恶意编码冗余信息以猜测目标参与者的训练数据,这是通过秘密共享指标向量无法阻止的。
差分隐私 (DP)。
差分隐私是一种通过描述类的模式同时保留有关个人的信息来公开共享有关数据集的信息的系统。DP是一种常用的隐私保护系统。DP不能用于防御反向和攻击,因为它只能保护单个敏感示例的隐私,而不能保护整个数据集(即部分订单)的隐私。
差分隐私主要可以应对成员推理攻击。至于反向乘法攻击,DP可能会粗略地保护目标参与者的私有敏感数据集。然而,对手仍然可以推断出添加DP噪声的数据集,并使用此数据集来训练等效模型。
备注
ML model:An ML model is a mathematical model that generates predictions by finding patterns in your data. (AWS ML Models) ML Models generate predictions using the patterns extracted from the input data.
[1] Qiang Yang, Yang Liu, Tianjian Chen, and Yongxin Tong, “Federated Machine Learning: Concept and Applications,” Feb. 2019. Available: https://arxiv.org/abs/1902.04885
[2] 杨强,刘洋,陈天健,童咏昕,“联邦学习”,Nov. 2018. Available: https://dl.ccf.org.cn/institude/institudeDetail?id=4150944238307328&from=groupmessage&isappinstalled=0&_ack=1, or https://wemp.app/posts/a3771dc7-6722-4690-bf25-23ba36f7b78c?utm_source=latest-posts
[3] 数据分析综述:联邦学习中的数据安全和隐私保护问题,Available:https://www.cnblogs.com/shujufenxianli/p/15937411.html
[4] 图像模型反向攻击,gitee Available:https://gitee.com/qmckw/reverse-attack/tree/master/
[5] 联邦学习实战,Available:https://github.com/FederatedAI/Practicing-Federated-Learning