基于粒子群算法优化的ELMAN动态递归神经网络预测-附代码
基于粒子群算法优化的ELMAN动态递归神经网络预测及其MATAB实现
文章目录
- 基于粒子群算法优化的ELMAN动态递归神经网络预测及其MATAB实现
- 1. 模型与算法描述
-
- 1.1 ELMAN神经网络预测模型介绍
- 1.2 粒子群算法PSO介绍
- 2. 粒子群算法PSO优化ELMAN回归预测模型的构建过程
-
- 2.1 模型的建立
- 2.2 算法流程
- 3. PSO-ELMAN回归预测模型的参数设置
- 4. 运行结果
- 5. MATLAB代码
1. 模型与算法描述
1.1 ELMAN神经网络预测模型介绍
ELMAN神经网络具有较强的非线性和泛化能力,与传统的前向神经网络相比,增加了承接层,即ELMAN具有四层网络结构:输入层、隐含层、承接层和输出层。承接层使得ELMAN神经网络有动态运算的特点与具有记忆功能,其结构与各网络层作用的详细说明,请参考博客:ELMAN神经网络及其matlab代码实现。
{ X ( k ) = f ( W 1 U ( k − 1 ) + W 2 X c ( k ) + b 1 ) X c ( k ) = X ( k − 1 ) Y ( k ) = g ( W 3 X ( k ) + b 2 ) \left\{\begin{array}{l} X(k)=f\left(W_{1} U(k-1)+W_{2} X_{c}(k)+b_{1}\right) \\ X_{c}(k)=X(k-1) \\ Y(k)=g\left(W_{3} X(k)+b_{2}\right) \end{array}\right. ⎩⎨⎧X(k)=f(W1U(k−1)+W2Xc(k)+b1)Xc(k)=X(k−1)Y(k)=g(W3X(k)+b2)
式中,U(k-1)、X(k)、Y(k)和Xc(k)分别为ELMAN的输入向量、隐含层的输出向量、输出层和承接层的输出向量。W1、W2、W3以及b1、b2分别为输入层到隐含层、承接层到隐含层、隐含层到输出层的连接权值矩阵,以及隐含层、输出层的阈值向量。
1.2 粒子群算法PSO介绍
粒子群优化算法(Particle Swarm optimization,PSO)是一种经典的启发式算法,由Kennedy等于1995年提出。基本思想是利用群体中的个体对信息的共享,从而使得群体位置在解空间中产生从无序到有序的演化过程,从而获得问题的最优解。粒子群算法的核心为速度更新与位置更新公式:
v ( d ) = w ∗ v ( d − 1 ) + c 1 ∗ r 1 ∗ ( pbest ( d ) − x ( d ) ) + c 2 ∗ r 2 ∗ ( gbest ( d ) − x ( d ) ) , ( 1 ) v(d)=w^{*} v(d-1)+c 1^{*} r 1^{*}(\text { pbest }(d)-x(d))+c 2^{*} r 2 *(\operatorname{gbest}(d)-x(d)),(1) v(d)=w∗v(d−1)+c1∗r1∗( pbest (d)−x(d))+c2∗r2∗(gbest(d)−x(d)),(1)
x ( d ) = x ( d − 1 ) + v ( d − 1 ) ∗ t , ( 2 ) x(d)=x(d-1)+v(d-1)^{*} t,(2) x(d)=x(d−1)+v(d−1)∗t,(2)
式中,d为当前的迭代次数,pbest为当前的最优粒子位置,gbest为历史的最优粒子位置,w为惯性权重,用于保持粒子的速度影响,c1,c2分别为个体学习因子和社会学习因子,v(d-1)为第d-1次迭代的粒子速度,x(d)为第d次迭代的粒子位置,r1和r2是(0,1)内的随机数。
粒子群算法的实现步骤为:
Step1:初始化最大迭代次数N,种群大小n,学习因子c1、c2,惯性权重w等参数。
Step2:初始化种群位置,计算初始的粒子适应度,并且获得初始最优个体。
Step3:Start Loop(K=1):使用公式(1)、(2)更新粒子的速度和位置。
Step4:计算种群的适应度值,更新当前种群最优粒子位置。
Step5:更新全局(迄今)最优的粒子位置和适应度。
Step6:执行步骤3-5,直至K>N,End Loop(跳出循环)。输出最优的个体位置与最优适应度值。
粒子群算法PSO优化实例理解:
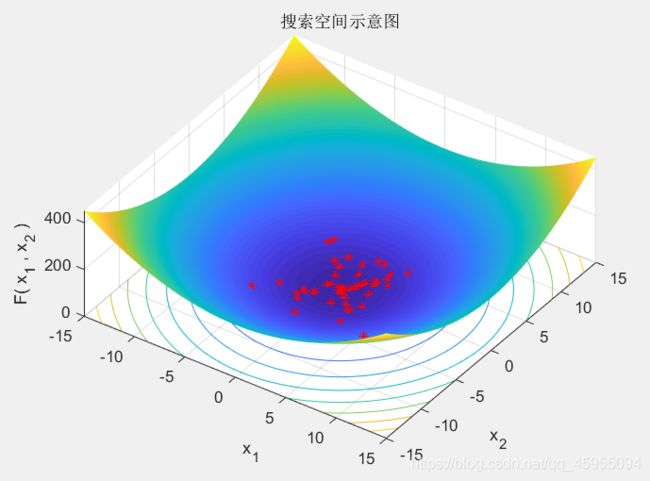
经过有限次迭代后,粒子群算法的种群中每个个体位置都会朝着最优解靠近,如下图所示:
%% PSO主程序
%________________________
% 初始化
clear
close all
clc
% 绘制搜索空间
x1 = -15:0.1:15;
x2 = -15:0.1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2;
figure(1),surfc(x1,x2,y,'LineStyle','none'),view(30,60)
xlabel('x_1');ylabel('x_2');zlabel(['F( x_1 , x_2 )']);title('搜索空间示意图')
hold on % 维持在图像上作图,用于后续散点图效果
% 初始化PSO参数
N = 100; %最大迭代次数
n = 50; % 粒子数量(种群大小)
dim = 2; % 变量个数
c1 = 2; c2 = 2; %个体学习因子 社会学习因子
w = 0.9; % 惯性权重
vmax = [6 6]; % 最大速度
lowerbound = [-15 -15]; upperbound = [15 15]; %范围
% 初始化位置和速度
x = zeros(n,dim); %位置
for i = 1: dim
x(:,i) = lowerbound(i) + (upperbound(i)-lowerbound(i))*rand(n,1);
end
v = -vmax + 2*vmax .* rand(n,dim); % 速度
% 计算每个个体的适应度
fitness = zeros(n,1);
for i = 1:n
fitness(i) = Object_function(x(i,:));
end
pbest = x; %当前最优
index = find(fitness == min(fitness), 1); %初始的最佳适应度个体索引
gbest = x(index,:); %迄今最优
% h:图窗句柄,绘制粒子的散点图
h = scatter3(x(:,1),x(:,2),fitness,'*r');
%% 开始进化
fitnessbest = zeros(N,1);
for d = 1:N
for i = 1:n
%速度更新
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));
% 速度越界调整
v(i,:) =limitbound(v(i,:) ,-vmax,vmax);
%位置更新
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
%位置越界调整
x(i,:) =limitbound(x(i,:),lowerbound,upperbound);
%更新个体适应度
fitness(i) = Object_function(x(i,:));
%更新当前种群的适应度
if fitness(i) < Object_function(pbest(i,:))
pbest(i,:) = x(i,:); %当前种群最优位置
end
%更新迄今最佳适应度
if Object_function(pbest(i,:)) < Object_function(gbest)
gbest = pbest(i,:); %历史最优位置
end
end
fitnessbest(d) = Object_function(gbest); %存储进化信息
pause(0.1) % 暂停0.1s
%绘制粒子运动散点图
h.XData = x(:,1);h.YData = x(:,2);h.ZData = fitness; % X Y Z 坐标
end
figure(2)
plot(fitnessbest,'r-','linewidth',2) % 绘制出每次迭代最佳适应度的变化图
xlabel('进化代数');ylabel('最佳适应度');title('PSO的进化曲线')
disp('最优解:'); disp(gbest)
disp('最优值:'); disp(Object_function(gbest))
%________________________________________
%子函数:用于范围约束
function x=limitbound(x,lb,ub)
for i=1:length(x)
if x(i)>ub(i),x(i)=ub(i);elseif x(i)<lb(i),x(i)=lb(i);else,x(i)=x(i);end
end
end
%子函数:目标函数(适应度函数)
function y= Object_function(x)
y=sum(x.^2);
end
2. 粒子群算法PSO优化ELMAN回归预测模型的构建过程
2.1 模型的建立
使用神经网络进行预测建模时,初始的权值和阈值一般由伪随机数初始化,使得训练数据训练好的模型性能不稳定。针对ELMAN神经网络的预测精度受权值和阈值的影响较大,使用粒子群优化算法PSO对参数进行优化,提高ELMAN神经网络的预测精度。
PSO-ELMAN预测模型的适应度函数取为训练集与测试集整体的均方误差,计算公式如下:
min f ( W 1 , W 2 , W 3 , b 1 , b 2 ) = 1 n 1 ∑ i = 1 n 1 ( y trainingSet ( i ) − y ^ trainingSet ( i ) ) 2 + 1 n 2 ∑ i = 1 n 2 ( y testingSet ( i ) − y ^ testingSet ( i ) ) 2 2 \min f\left(W_{1}, W_{2}, W_{3}, b_{1}, b_{2}\right)=\frac{\sqrt{\frac{1}{n_{1}} \sum_{i=1}^{n_{1}}\left(y_{\text {trainingSet }}(i)-\hat{y}_{\text {trainingSet }}(i)\right)^{2}}+\sqrt{\frac{1}{n_{2}} \sum_{i=1}^{n_{2}}\left(y_{\text {testingSet }}(i)-\hat{y}_{\text {testingSet }}(i)\right)^{2}}}{2} minf(W1,W2,W3,b1,b2)=2n11∑i=1n1(ytrainingSet (i)−y^trainingSet (i))2+n21∑i=1n2(ytestingSet (i)−y^testingSet (i))2
式中,n1和n2分别为训练集的样本数与测试集的样本数。粒子群算法在进化过程中,适应度越小,说明训练的模型准确,且对预测样本的精度有所提升。
2.2 算法流程
2.2.1 数据说明:
采用深度学习常用的建筑物能源数据集进行预测实验,数据是EXCEL格式,形式为:
| 样本序号 | 输入指标1 | 输入指标2 | … | 输出指标 |
|---|---|---|---|---|
| 1 | - | – | – | – |
| 2 | - | – | – | – |
| … | - | – | – | – |
| n | - | – | – | – |
2.2.2 算法步骤
步骤1:输入影响因素数据与目标输出数据,ELMAN神经网络划分训练集与测试集,对数据归一化处理,公式为:
x ′ = a + x − x min x max − x min × ( b − a ) x^{\prime}=a+\frac{x-x_{\min }}{x_{\max }-x_{\min }} \times(b-a) x′=a+xmax−xminx−xmin×(b−a)
式中, x ′ 是归一化后的数据, x , x min , x max , 分别为原始数据,及其最大值,最小值, a , b 分别为归一化后的最大值和最小值,如归一化至[0,1]范围内。 {\text {式中, }}x^{\prime}\text {是归一化后的数据,}x,x_{\min },x_{\max },\text{分别为原始数据,及其最大值,最小值,}a,b\text{分别为归一化后的最大值和最小值,如归一化至[0,1]范围内。} 式中, x′是归一化后的数据,x,xmin,xmax,分别为原始数据,及其最大值,最小值,a,b分别为归一化后的最大值和最小值,如归一化至[0,1]范围内。
步骤2:构建ELMAN神经网络,初始化网络结构。
步骤3:粒子群算法参数初始化。初始化最大迭代次数N,种群大小n,以及c1,c2,w参数。
步骤4:初始化粒子群算法PSO的种群位置。根据步骤2的网络结构,计算需要优化的变量元素个数。
步骤5:使用粒子群算法优化。将适应度函数设为ELMAN预测的均方误差。执行PSO的循环体过程,即速度更新和位置更新,直至达到最大迭代次数,终止粒子群优化算法。
步骤6:将PSO优化后的权值和阈值参数,赋给ELMAN神经网络。(或者在循环体当中,将网络结构理解为优化变量,输出最优的网络结构)。
步骤7:PSO优化后的ELMAN神经网络训练和预测,并与优化前的ELMAN神经网络进行预测误差分析和对比。
2.2.3 算法流程
![]()
3. PSO-ELMAN回归预测模型的参数设置
3.1 ELMAN神经网络参数设置
%网络参数配置
net.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.0001
net.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次
net.trainParam.mc=0.01; % 动量因子
net.trainParam.min_grad=1e-6; % 最小性能梯度
net.trainParam.max_fail=6; % 最高失败次数
3.2 粒子群算法参数设置
popsize=30; %初始种群规模
maxgen=50; %最大进化代数
dim=inputnum*hiddennum_best+hiddennum_best*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+outputnum; %自变量个数
lb=repmat(-3,1,dim); %自变量下限
ub=repmat(3,1,dim); %自变量上限
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
3.3 权值和阈值元素的编码
启发式算法在求解问题最优解时,常用的有三种编码方式:二进制,向量,以及矩阵。由于权值为矩阵形式,阈值为向量,为了统一,将权值矩阵和阈值向量的元素取出,存放于向量中,决策变量为1×n的向量形式。使用粒子群算法优化后,再将相应的元素从最优解向量中取出,按提取时的顺序放回到权值和阈值中。
w1=x(1:inputnum*hiddennum); %输入层到隐含层的权值元素
w2=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum*hiddennum); %承接层到隐含层的权值
B1=x(inputnum*hiddennum+hiddennum*hiddennum+1:inputnum*hiddennum+hiddennum*hiddennum+hiddennum); %隐含层到输出层的权值元素
w3=x(inputnum*hiddennum+hiddennum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum*hiddennum+hiddennum+hiddennum*outputnum); %隐含层的各神经元阈值元素
B2=x(inputnum*hiddennum+hiddennum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum*hiddennum+hiddennum+hiddennum*outputnum+outputnum); %输出层的各神经元阈值元素
4. 运行结果
4.1 粒子群算法的进化曲线
![]()
4.2 PSO-ELMAN预测与优化前ELMAN预测的误差对比分析
![]()
![]()
5. MATLAB代码
见博客主页