基于K-means的图像分割（python代码详解）

本文主要借鉴了下面文章，对下文的一些代码在本文进行了详细解释

机器学习十大经典算法之K-means (图像分割，python)_Mr.Q的博客-CSDN博客_kmeans图像分割python十大经典算法分别为：K-means K均值（无监督算法，聚类算法，随机算法）KNN(K Nearest Neighbor) K近邻（有监督算法，分类算法）逻辑回归（分类算法）决策树（有监督算法，概率算法）随机森林（集成算法中最简单的,模型融合算法）朴素贝叶斯EM算法Adaboost(集成算法之一)SVM马尔可夫一、算法过程（1）随机选择...https://blog.csdn.net/jizhidexiaoming/article/details/89214614?spm=1001.2014.3001.5506

一、“  K”和“means”

        K：有k个质心（簇）。

        means：质心是一个簇所有点的均值。

        K-means属于硬聚类。硬聚类指数据只能属于一个簇，与软聚类：数据可以不同程度的属于多个类相反。

二、算法步骤

        S1：选取初始质心：从样本点中随机抽取K个点作为质心。

        S2：所有样本点归类：计算所有样本点到K个质心的距离，将其划分到与其距离最近的簇中心所在簇。

        S3：重新确定质心：新质心 = 簇内所有点的均值。

        S4：循环更新：重复步骤S2,S3，直到质心不再变化。

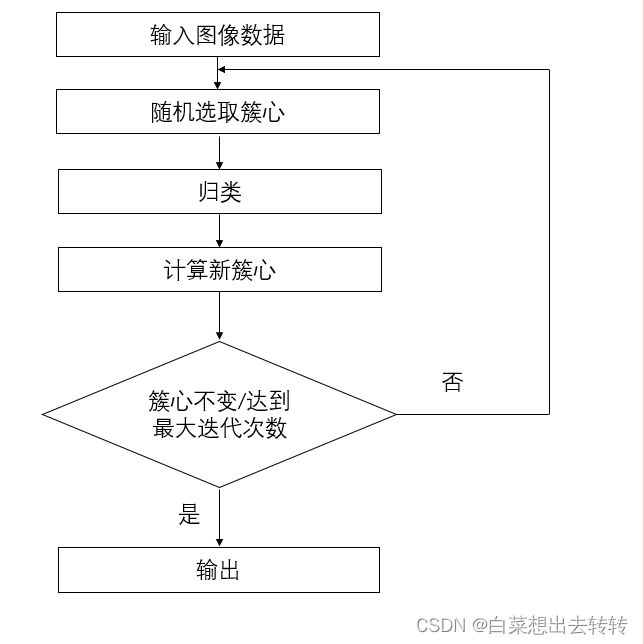
三、流程图

四、代码

import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('1.jpg')
row = img.shape[0]
col = img.shape[1]
plt.subplot(121)
plt.imshow(img)
	

def knn(data, iter, k):
    data = data.reshape(-1, 3)
    data = np.column_stack((data, np.ones(row*col)))
    # 1.随机产生初始簇心
    cluster_center = data[np.random.choice(row*col, k)]
    # 2.分类
    distance = [[] for i in range(k)]
    for i in range(iter):
        print("迭代次数：", i)
        # 2.1距离计算
        for j in range(k):
            distance[j] = np.sqrt(np.sum((data - cluster_center[j])**2, axis=1))
        # 2.2归类
        data[:, 3] = np.argmin(distance, axis=0)
        # 3.计算新簇心
        for j in range(k):
            cluster_center[j] = np.mean(data[data[:, 3] == j], axis=0)
    return data[:, 3]


if __name__ == "__main__":
    image_show = knn(img, 100, 2)
    image_show = image_show.reshape(row, col)
    plt.subplot(122)
    plt.imshow(image_show, cmap='gray')
    plt.show()

五、代码怎么使用？

        第一步，需要把待分割图片放入项目文件，like this:

         第二步，代码的第三行：'img = plt.imread()'，在括号里加入图片路径：“图片名.文件格式”，比如，1.jpeg、2.bmp等等。

六、运行结果

1.迭代100次，簇总数=5 

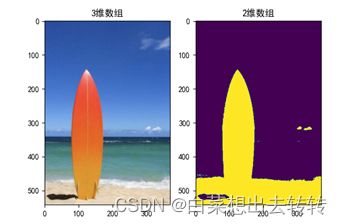
2.迭代10次，簇总数=2

七、核心代码解释

7.1图片信息处理过程 

7.1.1图片→ 三维数组(图片高，图片宽，3)

	img = plt.imread(‘path’)

7.1.2 三维数组(图片高，图片宽，3)→二维数组(图片宽*高，3)

	img = img.reshape(-1, 3)

7.1.3(-1, 3)数组 →（-1,4）数组

新增1列用来存储分类信息

	img = np.column__stack((img, np.ones(row*col)))

7.1.4 kmeans算法返回结果

只返回所有像素点的分类结果

	return img[:, 3]

7.2用数组表示图片

7.2.1描述像素点

        一维数组[R, G, B]就可以表示一个像素点，数组内容是三原色的取值，数组元素大小∈[0, 255]。

7.2.2描述图片

        一个三维数组就可表示一张图片，如果图片的分辨率为m*n，那么数组形状为(n, m, 3)。这个三维数组描述了图片所有像素点（共m*n个）的RGB信息。

(n, m, 3):n个形状为(m, 3)的2维数组。
n:图片的高
m:图片的宽
3:[RGB]长=3

7.3plt.imread()

7.3.1语法

img = plt.read(‘图片路径’)

7.3.2功能

        把图片的信息提取到数组中（将图片转化为数组）。

7.3.3返回值类型

        返回值类型：numpy数组

7.3.4返回值内容

        假设图片分辨率=m*n，宽*高

1. 如果是灰度图，返回（n, m）形状2维数组。
2. 如果是RGB图像，返回（n, m, 3）形状的三维数组。

7.3.5例

        读取照片，并获取包含该图片所有信息的3维矩阵。

        该照片的分辨率=371*543

import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('1.jpg')   # 读入图片
print(img.shape, type(img))
print(img) 
plt.imshow(img) # 利用数组显示图片
plt.show()
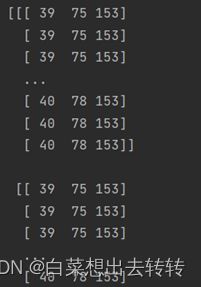
输出：(543, 371, 3) 
输出：img记录着所有像素点的RGB值：

 7.4plt.imshow()

7.4.1功能：数组->图片

        将数组存储的RGB信息映射为彩色图片。

7.4.2语法

plt.imshow(img,  cmap='gray') 
plt.imshow(img) # hsv图片
plt.show()

        img是包含图片所有信息的三维数组。

        plt.imshow()中的cmap参数有两种取值：gray(灰度表示)，hsv(hsv颜色空间)，默认值是hsv。

7.4.3数组形状

        (1)三维：从图片提取的数组是三维，可以由plt.imshow()正常显示。

        (2)二维： 图像分割的结果是二维数组，数组每个元素对应一个像素点的种类。如果图像有3种簇，那么二维数组的取值是[0, 1, 2]，代表归属不同的种类。

7.4.4不同数组形状显示的图片特点

        不论是二维还是三维数组，用plt.imshow(img)表示时，如果不设置cmap参数，默认都是hsv。

        特别地，二维数组显示的图片的颜色种类和二维数组元素可取值的数量是一样的，这样就可以区分分割的结果。下面，是两种簇的分割。

7.5plt.show()

7.5.1作用

        显示图片。

7.5.2特点：阻塞

        plt.show()被执行时，程序就被阻塞在这一行不向下进行，直到图像窗口被关闭时，程序才往下进行。

7.6随机产生簇心

7.6.1二维数组索引

        一般情况下，对于二维数组，用1个或者1对数字分别索引数组某行或者某个元素。

        也可以用向量进行索引，得到的是指定行构成的数组。

        下面，用向量对二维数组进行索引：

import numpy as np
x = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
print( x[0] ) #[1, 2]
print( x[0,0,] ) # 1
print( x[[0, 1, 2]] ) #[[1, 2], [3, 4], [5, 6]]

7.6.2随机产生k个簇心

        先从[0, row*col-1]中随机产生长度为k的向量，再在data中索引该向量，得到k个随机点

distance = np.sqrt(np.sum((x - y)**2, axis=1))

作为簇心。

cluster_center = data[np.random.choice(row*col, k)]
#row = data.shape[0]
#col = data.shape[1]

7.7.欧氏距离

7.7.1欧氏距离定义

7.7.2实现

distance = np.sqrt(np.sum((x - y)**2, axis=1))

7.7.3注意：同列不同行的数组可以进行加减法。

        计算图片RGB数组和一个簇心距离，二者形状分别为：[n, 3]和[1, 3]。

import numpy as np
x = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
y = np.array([1, 2])
print(x-y)
输出：
 

 

7.8归类

7.8.1思路

        将三维数组另起一列，放像素点的归类信息。属于第k个簇，归类信息就存储为k。

        最终K-means返回的结果：每个像素点对应的信息只有它属于哪个类，取值范围为[0, k-1]。

7.8.2实现

        np.argmin:返回一行/列中最小元素的索引。

data[:, 3] = np.argmin(distance, axis=0)

7.9计算新簇心

7.9.1原理

        簇心 = 簇内所有点的平均值，簇心并不一定是实际存在的像素点的RGB取值。

7.9.2实现

for j in range(k): # k为簇的个数
	cluster.center[j] = np.mean(data[data[:, 3] == j], axis=0)

        其中，data[data[:, 3] == j]：返回全部有指定元素的行。