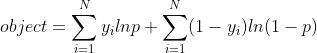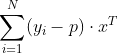逻辑回归(Logistic Regression)详解(附代码)---大道至简之机器学习算法系列——非常通俗易懂！

（不愿意看我废话的直接跳到正文处(*^▽^*)）

很多小伙伴说：逻辑回归？太简单了！我懂的不要不要的，就是sigmoid函数！没毛病，就是sigmoid函数。事实上，大部分机器学习算法，网上不仅有好用的现成的开源包，而且大体原理也能看懂，但是，就我个人理解，学习机器学习算法 ，最最最重要的是要学会它怎么来的，咋想出来的，它诞生的思路是啥？沿着这个倒推思维去学，不仅快，而且记忆能更加深刻。而至于它的使用，已经有优秀的开源包，我们就没必要重复造轮子啦。

目录

总结

1. sigmoid函数

2. LR的损失函数

3. 损失函数的优化

4. 代码 

---

文档撰写习惯，这里先抛出总结：

总结

1. LR模型定义：

2. LR目标函数：

3. 目标函数的梯度：

4. 梯度的优化：梯度上升

5. 优缺点：

优点：可解释性强、sigmoid函数数学特性好，值域0~1，是凸函数、形式简单，学习快；

缺点：由于形式简单，无法很好的拟合复杂数据、不能很好的处理非线性问题；

6. 虽然叫逻辑回归，但其实它是个分类算法，预测的是概率值，不是真值；

1. sigmoid函数

逻辑回归为啥要用sigmoid函数？我们都知道，对于二元一次方程在二维平面上是一条直线，这条直线的作用是，当a和b一定时，给定一个x，就会有对应的一个y，假设x为某个训练样本特征，那么得到的y或>0，或<0，或=0，规定大于等于0的为正标签，小于0的为负标签，这样就完成了一次简单的分类。同理可得，当方程为多元方程

时，代表超平面，则可以通过梯度下降法学习得到w和b，从而确认分类决策函数，梯度下降法非本文重点，请自行查阅相关资料，或参考统计学习方法P39。

但是，如果仅仅是靠输入一组变量，得到一个y这种方式，我们可以认为，y的值域为R，这样对决策很不友好，因为y的值有可能非常大，另外，很多时候当我们还想要知道当输入一组变量时，得到的某个决策类别的概率是多大，越大说明决策的准确性越高，显然这种输入-输出的方式是无法做到的。所以，一个自然而然的思路就是，给决策函数一个输入，决策函数给你一个0~1之间的概率值，然后你自己定一个阈值，比如0.5，大于0.5的我们认为是正类，小于等于0.5的认为是负类，那么越比0.5大，就越说明决策函数给出的正类的可信度越高，反之亦然。这样不仅灵活，而且可以根据数据情况调整不同的阈值来达到最佳准召率。

为解决上述提到的需求，我们很自然的想到，等式左边应当是个0~1的值，且该值能反映样本属于某一类别的概率。现在我们假设p为样本属于正类的概率，则样本属于负类的概率为1-p，为了清楚属于正类的概率比属于负类的概率大多少，我们用p/(1-p)来表示这一需求，现在，我们为这一比值加上一个对数，就有了如下形式：

                                                                                                               （公式1）

上式即我们所谓的对数几率。这里需要说明的一点，为什么要取对数，我个人从创始人的思路源头上还不是那么清楚，暂且认为是个数学习惯罢了（别钻牛角尖哈）。

现在回到我们最初的需求，即让函数  满足：给定等式右边的x，左边能够输出一个概率值。现在我们假设得到了这么一个函数形式，事实上这个假设是成立的，那么结合公式1，我们得到如下式子：

                                                                                                            （公式2）

现在我们来分解一下这个式子，看看如果在公式2存在的条件下，我们的p等于什么：

两边同时取e，得到：

                                                ​​​​​​​        ​​​​​​​                                                         （公式3）

（为了方便，后续的b我们都放在向量w中，这种操作其实就是在原有的w向量最后多加一列，值为b，并在原有的x向量最后多加一列，值为1，这样一来两个向量做点乘时得到的结果和把b单独拉出来加在w和x点乘结果的后面是一样的，细节这里不再赘述。）

 公式3左右移项，化简，得到：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​                                                  （公式4）

 则1-p即取得负类的概率值为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                                （公式5）

至此，逻辑回归内容中最重要的部分我们推理结束。注意看公式4，我们上下同时除以  ，就得到了我们大家熟悉的著名的sigmoid函数：

而公式4和公式5合起来称为逻辑斯蒂回归模型。通常，我们只需要用到公式4，可以看出，所谓的逻辑回归，不过是对原始函数形式做了一些变换，其实就是sigmoid函数。在这里，我们需要补充一个非常重要的结论（面试常考）：

 我们对sigmoid函数求导，这之前，我们稍微对w和x的点乘做一下变换，即 ，这是矩阵能够点乘的必要条件决定的，于是：

也就是说，对于sigmoid函数求导，有这样的结论，这个结论请记住！

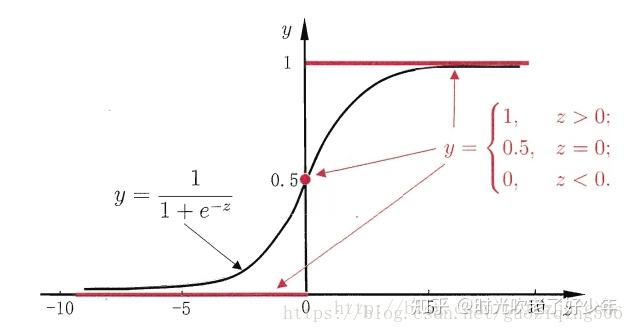
sigmoid函数图像：

 sigmoid导数图像：

以上图像均来源于网络。从sigmoid函数图像上可以看出，sigmoid能够把任意输出值压缩在0~1的范围内，其中，当输入为0时，输出值取得中点0.5，其导数达到极值，通常我们会以此为分界点来划分正负类别，这也是sigmoid函数的另一解释。 

2. LR的损失函数

在第一节中，我们详细解释了逻辑回归函数的由来，推导出了sigmoid函数表达式，并推导了sigmoid的导数形式，那么对于一个决策学习过程来讲，其优化目标是必不可少的，接下来我们要来看看逻辑回归算法的损失函数以及优化过程。

假设一个数据集 ，为第i个输入样本，为对应的真值取0或1，0代表负类，1代表正类，现在对于这个数据集，我们希望输入的每一个x，其输出对应的y的概率最大，即让

最大 ，其中  为样本为正类的概率；这个表达式是说，当预测值为正类，则=1，那么，反之则。由于函数表达式中有连乘符号，习惯上，我们取对数，变连乘为加和，令：

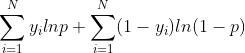        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                          （公式6）

至此，我们推出了形如公式6的LR的损失函数，可以看出，该函数实际上属于对数似然函数，y是真值，p是我们的预测值。

3. 损失函数的优化

第二节中，我们已经得到了LR的损失函数，函数中存在w和b两个参数，现在我们要优化它，就是对模型参数进行估计，它是对数似然函数，那自然就是要用最大似然估计。想想我们学过的最大似然估计方法，无非就是分别对待估计的参数求偏导，再分别令求导结果等于0，以此求得w和b。

为了方便，我们先把求和符号去掉：

（1）对w求偏导

 

 

把求和符号放回去，就得到：

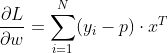        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                            （公式7）

（2）对b求偏导

同理得到：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                                  （公式8）

一定有小伙伴会问x^T怎么来的，这里补充一个结论：

对于公式7和公式8，由于我们直接求w并不好求，所以我们这里需要使用梯度上升法，之所以利用梯度上升而非梯度下降，是因为我们这里要求的是最大似然值，所以更准确的应该说我们是在优化目标函数而非损失函数，当然，你给目标函数加上负号，就可以转化成求梯度下降啦。另外，由于我们已经将b归并到w中了，因此我们这里只需要优化公式7即可，只要给定初始值，w和b就会一起进行梯度更新。

梯度上升：

其中，lr为学习率。

4. 代码 

第三节中，我们得到了优化目标函数以及优化方法，这里总结一下，整个逻辑回归算法，我们核心要优化的就是

当我们给定w的初始值、学习率、迭代轮次，然后套用梯度上升公式，就可以计算目标w，并得到一个决策函数。这里w的维度应该增加一维存放b，话不多说，上代码，这里我只列出了两个我认为需要注意的函数，第一个是数据处理阶段，注意看`load_data`这个方法，我在生成data的时候，在data的最后一个位置加了一个1，这是b的初始值；第二个是逻辑回归算法函数，代码很简单我就不解释了，完整代码：逻辑回归算法

def load_data(self, opt='train'):
	"""
	加载数据，根据自己的数据格式做相应修改，这里主要使用mnist数据集
	:param opt: 控制是否为有标签数据训练/预测，可选train、test、predict（无标签）
	:return: data or data、label
	"""
	df = pd.read_csv(self.fpath, keep_default_na=False, header=None)
	data = []
	labels = []
	for row in tqdm(df.iterrows(), total=len(df)):
		l = row[1].tolist()
		if opt == 'train' or opt == 'test':
			# 归一化特征值（可选），但是归一化后加速收敛，效果较好
			data.append([int(x)/255 for x in l[1:]] + [1])
			labels.append(1 if row[1].tolist()[0] == 0 else 0)
		else:
			data.append([int(x)/255 for x in l] + [1])
	return torch.Tensor(data), labels if opt == 'train' or opt == 'test' else torch.Tensor(data)

def logistic_regression(self, x, w, label):
	"""
	逻辑回归计算
	:param x: 训练样本，[1, hidden_size]
	:param w: 权重，float
	:param label: 标签，int
	:return: w
	"""
	x = torch.transpose(x, 0, -1)
	w_x = torch.matmul(w, x)
	y_x = label * x
	# 根据统计学习方法6.1.3公式对w求偏导后的结果
	logic_func = y_x - np.exp(w_x)*x / (1 + np.exp(w_x))
	# 特别注意，由于是求极大似然值，而不是loss，因此这里应当使用梯度上升而非梯度下降
	w += self.lr * logic_func
	return w

在测试阶段，我们已经有了训练好的w权重，套用sigmoid函数，我们输入一个样本，就会有一个预测概率值输出，可以规定概率值>0.5的为正类，反之为负类，自己定。

感谢小伙伴的阅读，本人非数学专业，因此文章中许多细节之处写的不够严谨，而且很多地方都解释的很通俗，不够科学严谨，还请大佬们多多指教多多谅解，有错误之处请提出您的宝贵意见，感谢支持！

---

参考文献：

[1] 《统计学习方法》第二版 李航