CrowdPose: Efficient Crowded Scenes Pose Estimation and A New Benchmark

非常感谢知乎 不破勝光的论文精读 很值得一看~（大佬呀），本文是是自己的学习笔记，加深理解，嘿呀

论文翻译

1. 摘要

多人姿态估计是许多计算机视觉任务的基础，近年来取得了显著进展。然而，以往的方法很少探讨拥挤场景中的姿态估计问题，而在许多场景中这仍然是一个具有挑战性且不可避免的问题。此外，目前的基准无法为这种情况提供适当的评价。在本文中，我们提出了一种新颖而有效的方法来解决人群中的姿态估计问题，并提出了一种新的数据集来更好地评估算法。我们的模型由两个关键部分组成：候选关键点单个体位姿估计(ioint-candidate SPPE)和全局最大关键点连接(global maximum joint sassociation)。通过每个关键点的多峰预测和基于图论模型的全局连接，该方法对拥挤场景中不可避免的干扰具有较强的鲁棒性，推理效率高。所提出的方法在CrowdPose数据集上以5.2 mAP超越了目前最先进的方法，在MSCOCO数据集上的结果证明了我们方法的泛化能力。源代码和数据集将公开。

2. 相关工作

对于多人姿态估计问题，有多个数据集，如MPII、MSCOCO、AI Challenger等。尽管这些数据集非常普遍，但它们存在低密度问题（a low-density problem），这使得当前的模型在非拥挤场景下过拟合。 最先进的方法的性能随着人类数量的增加而下降。

Part-Based Framework

综述了基于部分(part)的框架[4,21,18]的代表性工作。基于part的方法检测关键点并将它们与整个人关联起来。目前最先进的基于部分的方法主要是在关联方法上有所不同。Cao等人使用部分亲和力场和贪婪算法对关键点进行连接。帕潘德里欧等人的[21]检测个人关键点并预测用于关键的相对位移。Kocabas等人提出了一种多任务模型，通过pose残差网络将关键点分配给被检测人员。基于部分的关键点检波器由于只考虑局部小区域，输出的响应热图较小，因而相对易受攻击。

Two-Step Framework

我们的工作遵循两步法。两步方法首先检测人体提议框（human proposals ）[25,22]，然后执行单人姿态估计[20,33]。目前最先进的两步方法[8,32,13,14]的得分明显高于基于part的方法。然而，两步方法在很大程度上依赖于人类的检测结果，在拥挤的场景[26]中失败。当人们在人群中彼此靠得很近时，裁掉一个只能容纳一个人的边界框是不可能的。有些工作[11,1]是针对人群中的行人跟踪。作为补充，我们提出了一种新颖高效的方法，显著提高了拥挤场景中的姿态估计性能，对人体检测结果具有鲁棒性。

[8] Cascaded pyramid network for multi-person pose estimation.
[32]Simple baselines for human pose estimation and tracking（ECCV 2018）.
[13]RMPE: Regional multi-person pose estimation(ICCV 2017)
[14]Mask RCNN(ICCV 2017)

3. 方法

整体流程
论文中提出方法的pipeline：JC SPPE在训练阶段使用关键点候选loss函数。在推理阶段，JCSPPE接收人体proposals 并生成关键点候选。然后我们利用人体proposals 和关键点候选来构建一个人-关节图。最后，通过求解图模型中的分配，将关键点与人的提议框联系起来。

3.1.Joint-Candidates SPPE

JC SPPE接收一个行人proposal然后输出一组预测人体关键点位置的Heatmaps。尽管一个proposal应该只包含一个人，但是在密集场景中，我们不可避免的要处理许多来自其他proposal的关节点。之前的工作[32, 8, 13]采用SPPE（单人姿态估计）来抑制干扰的关节点。但是SPPE在密集场景中表现不佳。因为它们的感受野受到了输入行人proposal的限制。为了解决这个问题，我们提出了一种全局视角的全新的JC SPPE。

3.1.1 Loss Design
对于第 $i^{th}$个行人proposal，我们把它的区域 $R_i$ 输入我们的SPPE网络获得输出 $P_i$ 。$R_i$ 中有两个类型的关键点，即属于第 $i^{th}$ 个人的关节点，和不属于该人的关节点。我们把它们分别称为目标关节点（target joints）和干扰关节点（interference joints）。

我们的目标是增强目标关节的响应（Heatmap），抑制干扰关节的响应。但是，我们并没有直接对它们进行抑制，因为当前proposal的干扰关键点可以被视为其他proposal的目标关键点。因此，我们可以利用干扰关键点在全局上和其他行人估计一起预测行人姿态。因此，为了利用这两种候选关节，我们用两种不同的强度（intensities）输出它们。

Heatmap Loss: 对于第 $i^{th}$个人的第 $k^{th}$ 个joint，我们令目标 joint 的 Heatmap 为 $T_i^k$，其由一个2D高斯分布 $G\left({\mathbf{p}}_i^k|\sigma \right)$ 构成，该分布标准差 $\sigma$，中心位置为 $p_i^k$。

对于干扰关键点，我们令它们为集合 ${\Omega }_i^k$ 。干扰关键点的Heatmap记为 ${\mathbf{C}}_i^k$ ，由一个混合高斯分布 ${\Sigma }_{p\in {\Omega }_i^k}G(\mathbf{p}|\sigma )$ 组成。

我们的损失函数如下式所示：
$${\mathrm{Loss}}_i=\frac{1}{K}\sum _{k=1}^{K}MSE\left[{\mathbf{P}}_i^k,{\mathbf{T}}_i^k+\mu {\mathbf{C}}_i^k\right]$$
这里的 $\mu$ 是一个 [ 0, 1 ] 之间的衰减系数。如前所述，干扰关键点在其他行人实例的关节点预测中非常有用。因此，我们应该通过全局的角度来进行交叉验证。最后我们取 $\mu$=0.5 ，主要来自于我们的直觉：干扰关键点应该被抑制，但是不能被过于抑制。传统的 Heatmap Loss函数可以被视为 $\mu$=0 的特殊情况

3.1.2 讨论
传统的SPPE依赖于高质量的行人检测结果。它的任务是根据给定的人体proposal定位和识别干扰关键点。如果SPPE错把干扰关键点当成了目标关键点，那么这是一个不可逆转的错误。丢失的关节点将不会输入到后处理步骤中，比如pose-NMS。

我们提出的JC loss就是为了解决这一问题。这样的损失函数鼓励JC SPPE网络预测一个多峰值的Heatmap，然后把所有可能的joints设为候选关节点（joint candidates）。在密集人群情况下，传统的SPPE很难确定干扰关键点，JC SPPE仍然可以预测一系列的候选关节点（joint candidates）并且保证高recall。我们将在下一个步骤里解决匹配问题，这将用到全局的JC SPPE信息。

3.2.Person-Joint Graph

由于我们的关键点候选机制和来自行人检测器的冗余行人 proposal，关键点候选的数量要比实际关键点的数量大得多。为了减少冗余关节，我们构建了一个人-关节图（person-joint graph），并应用最大人-关节匹配算法来构造最终的人体姿态

图4：在密集人群环境下，行人proposals高度重合。重叠的行人proposal会倾向于预测同一个关节点。在这里的情况下，如果我们直接选择最高的Heatmap响应作为最后的姿态点，两个行人proposals会有相同的右膝盖和右腿。我们提出的匹配算法可以通过全局最优匹配解决这一问题。

3.2.1 Joint Node Building

由于高度重叠的行人proposal往往预测相同的实际关节(如图4所示)，我们首先将这些表示相同实际关节的候选节点作为一个节点进行分组。

通过高质量的关节点预测结果，表示同一个关节点的候选关键点（JC）通常都互相非常靠近。因此我们可以按照如下的方式对这些JC进行分组：给定两个JC $p_1^k$， $p_2^k$ 和控制偏差 ${\delta }^k$ ，如果满足下式：
$${\Vert p_1^{(k)}-p_2^{(k)}\Vert }_2\le \min \left\{u_1^k,u_2^k\right\}{\delta }^{(k)}$$

那么我们将它们标记为同一个点，这里的 $u_1^k,u_2^k$ 是两个JC在高斯 Heatmap 上的响应偏差。 是第 $k^{th}$ 个关节点的控制偏差的参数，这里我们直接采用MSCOCO[19]里的值。我们使用 $\min \left\{u_1,u_2\right\}$ 而不是常数阈值的原因是为了保证：当且仅当$p_1,p_2$ 同时落入各自的控制域（半径为 $u_1^k{\delta }^k,u_2^k{\delta }^k$ ）内，我们才将其划为一个。一个点可以通过上述的方式代表一组点。

通过将一个关节组构建为一个节点，我们得到了节点集（JC集合）
$$\mathcal{J}=\left\{v_j^k:\text{ for }k\in \{1,\dots ,K\},j\in \left\{1,\dots ,N_k\right\}\right\}$$

这里 $K$ 是任务里一个人的关节点数，COCO是17、MPII是16、Ai Challenger是14。$N_k$ 这里是一个关节点 $k$ 的候选点数，$v_j^k$ 是关节 $k$ 的第 个节点的一个集合。所有JC点在 $\mathcal{J}$中的总数是 。

3.2.2 Person Node Building

人体节点表示由人体检测器检测到的行人proposal。我们将person节点集表示为$\mathcal{H}=\left\{h_i:\forall i\in \{1\dots M\}\right\}$，其中 $h_i$ 为第 $i$ 个person节点，$M$ 为检测到的行人proposal数量。

理想情况下，一个合理的行人proposal会紧密的包裹一个实例。然而，在拥挤的场景中，这一条件并不总是得到满足。人类探测器将产生许多冗余的建议，包括截断和不紧凑的边界框。我们将在第3.3节的全局人-关节匹配中消除这些低质量的人体节点

3.2.3 Person-Joint Edge

在获得行人和关节点后，我们把它们连在一起形成我们的行人-关节图。如果一个关节点 $h_i$ 包含一个来自行人节点 的JC，那么我们在它们之间建立一条边 $e_{i,j}^k$ 。 $e_{i,j}^k$ 的权重是这个JC的响应值，由 $w_{i,j}^k$ 表示。在这种情况下，我们可以构造一个边集合 $\mathcal{E}=\left\{e_{i,j}^k:\forall i,j,k\right\}$ 。

这样一个行人-关节图可以表示为：
$$\mathcal{G}=((\mathcal{H},\mathcal{J}),\mathcal{E})$$

3.3. Globally Optimizing Assocation

从现在开始，我们估计人群中人类姿态的目标转化为在person-joint graph里找到有最大权值的子图。我们的目标函数是：

$$\begin{array}{c}{\max }_d\mathcal{G}={\max }_d{\sum }_{i,j,k}{w}_{i,j}^{(k)}\cdot d_{i,j}^k\\ \text{ s.t. }{\sum }_j{d}_{i,j}^k\le 1,\forall k\in \{1,\dots ,K\},\forall i\in \{1,\dots ,M\}\\ {\sum }_i{d}_{i,j}^{(k)}\le 1,\forall k\in \{1,\dots ,K\},\forall j\in \left\{1,\dots ,N_k\right\}\\ d_{i,j}^{(k)}\in \{0,1\},\forall i,j,k\end{array}$$

这里的 $d_{i,j}^{(k)}$ 表示在最后的图中是否保留边 $e_{i,j}^k$ 。约束方程(5)和(6)迫使每个行人的proposal只能匹配最多一个第 $k^{th}$ 节点。

注意这里的 $\mathcal{G}$ 可以分解为 $k$ 个子图 ${\mathcal{G}}_k=\left(\left(\mathcal{H},{\mathcal{J}}^{(k)}\right),{\mathcal{E}}^{(k)}\right)$，这里的 ${\mathcal{J}}^k=\left\{v_j^{(k)}:\forall j\in \left\{1\dots N_k\right\}\right\}$ 以及 ${\mathcal{E}}^k=\left\{e_{i,j}^{(k)}:\forall j\in \left\{1\dots N_k\right\}\right\}$ 。因此我们目标函数可以表示为：

$$\begin{array}{c}{\max }_d\mathcal{G}={\max }_d{\sum }_{i,j,k}{w}_{i,j}^{(k)}\cdot d_{i,j}^{(k)}\\ ={\sum }_{k=1}^K\left({\max }_{d^{(k)}}{\sum }_{i,j}{w}_{i,j}^{(k)}\cdot d_{i,j}^{(k)}\right)\\ ={\sum }_{k=1}^K{\max }_{d^{(k)}}{\mathcal{G}}_k\end{array}$$

如上式所示，求解全局的行人-关节图 $\mathcal{G}$ 上的匹配问题数学上等价于分别求解它的每个子图 ${\mathcal{G}}_k$ 。这里 ${\mathcal{G}}_k$ 是一个有行人子集和 $k^{th}$ 个节点子集组成的二向图。对于每一个子图，我们采用改进版的KM算法[6]来求解最优匹配问题。通过对每个 ${\mathcal{G}}_k$ 分别求解，我们可以获得最终的解集

注意：这里有个独立性假设，即一个目标检测，其对应的所有关键点相互独立。

给定一个图匹配的结果，如果 $d_{i,j}^{(k)}=1$ ，那么这个加权的中心 $v_j^k$ 被赋给第 $i^{th}$ 个行人proposal作为它的第 $k^{th}$ 个节点。这里，加权的中心意味着 $v_j^k$ 中JC坐标的线性组合并且权重为它们 Heatmap 响应分数。通过这种方式可以得到每个行人proposal。而不匹配任何节点的行人将被移除，这就消除了低质量的行人proposal

Computational Complexity: 在许多场景下姿态估计的前向推理速度都非常重要。我们证明了我们的匹配算法和一般的贪婪NMS算法具有相同的计算复杂度

由White和Whitely[29]证明了图模型的内在特性：如果一个图 $G$ 的每一个非空子图 $X$ 最多只有 $k|X|-l$ 条边，那么它是 $(k,l)-sparse$ 的。这里的 $|X|$ 是子图中节点的个数，而

考虑子图 ${\mathcal{G}}_k=\left(\left(\mathcal{H},{\mathcal{J}}^{(k)}\right),{\mathcal{E}}^{(k)}\right)$ 。它表示一个行人proposals和第 $k^{th}$ 个关节点的连接。根据我们的统计，如图5所示，在拥挤的场景中，每个人的Bounding Box最多只能容纳4个人。

换句话说，一个行人实例最多可以最多对4个节点建立边。换句话说，我们的行人-关节子图是 $(4,0)-sparse$ 的：

$$\left|{\mathcal{E}}^{(k)}\right|\le 4\left|{\mathcal{G}}^{(k)}\right|-0$$

由于我们的行人-节点图的稀疏性，我们可以很有效率的求解匹配问题。我们把 ${\mathcal{E}}^{(k)}$ 变换到一个联合矩阵 $M_{e^k}$ 中（其不相连的点为0）。根据Carpaneto[6]的研究成果，这个稀疏矩阵的线性匹配问题可以在 $\mathcal{O}\left(n^2\right)$ 也就是 $\mathcal{O}\left({\left(|\mathcal{H}|+\left|{\mathcal{J}}^{(k)}\right|\right)}^2\right)$ 的维度上求解。既然我们消除了重复检测，并且建立了行人和节点间一对一的对应关系，那么 $\left|{\mathcal{J}}^{(k)}\right|$ 的期望就是 $\left|\mathcal{H}\right|$ 。因此我们有 $\mathcal{O}\left({\left(|\mathcal{H}|+\left|{\mathcal{J}}^{(k)}\right|\right)}^2\right)=\mathcal{O}\left({\mathcal{H}}^2\right)$ 。这样计算的复杂度就和传统的贪婪NMS算法一样了。

3.4. Discussion

我们的方法使用了图模型的方法来对行人proposals和JC进行全局的匹配。行人proposals互相之间竞争关节点。这样，那些没有显著的行人实例的行人proposal不会被分配到任何关节点，因为它们的关节点的响应分数会相对比较低。因此，许多多余的和质量低的行人proposals会被删除。和我们的算法相比，传统的NMS是一种基于实例的贪婪算法，效率更低。尽管[3, 7, 13]中提出了pose-NMS利用姿态信息，它们的算法依旧是基于实例的，并不能解决丢失关节点和错误匹配问题。我们的全局优化算法可以很好的处理这种情况。

4. CrowdPose Dataset

在本章中，我们介绍我们的数据集CrowdPose，包括场景定义，数据收集过程和数据集的统计信息。

4.1. Crowding Level Definition

为了建立一个密集人群姿态 ，我们首先需要定义CI，也就是密集度。直觉上来图片中人的个数是一个不错的选择。但是密集人群姿态估计最主要难点并不在于目标个数，而是人群中的遮挡问题。因此，我们需要一个新的CI来表示密集的程度。在第 $i^{th}$ 个行人实例的框中，我们分别记属于该行人实例的关节点和不属于该行人实例的关节点的个数为：$N_i^a,N_i^b$ 。$N_i^a/N_i^b$ 则是这第 $i^{th}$ 个行人实例的CI。我们的CI通过对一张图片里所有行人的CI进行平均来获得图片的CI：
$$\text{ Crowd Index }=\frac{1}{n}\sum _{i=1}^n\frac{N_i^b}{N_i^a}$$
这里 $n$ 表示图片里行人的总数。

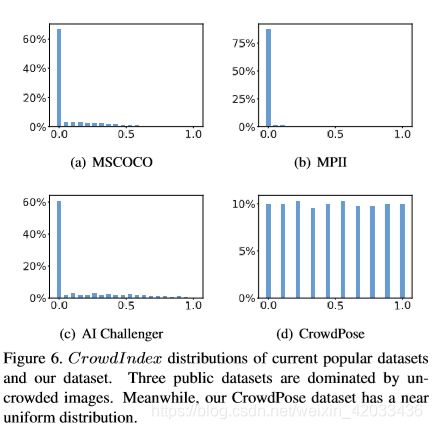
图6：现有的数据集和我们的数据集上CI的分布。这3个公开的数据集主要由非密集图片构成。同时，我们的CrowdPose数据集有着接近均一分布的CI。

我们在三份公开数据集：MSCOCO，MPII和AI Challenger。如图6所示，不密集的场景在这三份数据集上占主导。这说明目前主要的SOTA方法主要集中在非密集人群上，而忽略了密集人群的样例。

4.2. Data Collection

为了建立一个不同场景下的benchmark来推动模型适应不同场景，我们希望我们的benchmark能够覆盖不仅仅密集人群也能覆盖日常场景。因此我们首先分析了3份公开数据集[2, 19, 30]，然后根据它们的CI分为了20组，从0到1，不同组之间的CI的步长为0.05.然后我们对这些组均匀的采样30,000张图片。

4.3. Image Annotation

尽管这些图片都被标注了，它们的标注格式并不一样。以关节点为例，MSCOCO有17个关键点，而MPII有16个，AI Challenger有14个。同时，人类标注这在密集人群场景中更加容易犯错，因此我们对这些图片进行了重新标注：

• 我们使用14个关节点，然后对这30,000张图片进行了行人框和关键点标注；

• 我们分析了这30,000张图片在新的标注结果下的CI，然后选取了20,000张高质量的图片；

• 我们对这些图片中的每一个人进行了裁剪，并对每一个框中的推理点进行了标注；

我们使用了交叉标注，这样每张图片都至少有两个标注员对其进行标注。如果这两次标注有很大差异，那么我们视其为错误结果并对其重新标注。最后，我们对每个关键点位置进行平均来保证标注质量。

4.4. Dataset Statistics

Dataset Size: 我们的数据集总共包含20,000张图片，80,000行人。训练、验证、测试子集按照5:1:4的比例进行划分。

Crowd Index Distribution: CrowdPose中CI的分布如图6所示。和其他数据集不同的是，我们的CI服从[0, 1]之间的均匀分布。注意这里我们并不是简单的强制CrowdPose具有高CI。如果一个模型只在密集人群上训练，那么它在非密集人群上的表现可能会有下降。均一分布可以很好的帮助模型的泛化能力。

Average IOU: 我们还计算了行人框的平均IOU。可以发现我们的CrowdPose数据集平均IOU为0.27，而MSCOCO、MPII、AI Challenger只有0.06、0.11和0.12。

5. Experiments

在这一章我们首先介绍数据集和评估用的设置，然后我们展示了我们的结果并和SOTA的方法进行了比较，最后我们对我们的方法进行了对比实验。

5.1. Datasets

CrowdPose: 我们提出的CrowdPose数据集有20,000张 和80,000个行人。它的CI服从[0, 1]之间的均匀分布。CrowdPose数据集目标是提升模型在密集场景下的表现并将模型泛化到不同的场景中。

MSCOCO Keypoints: 我们同样在MSCOCO数据集上评估了我们的结果。目标关键点相似度OKS和IOU一样在计算关键点检测的AP/AR起到了重要的作用。我们考虑mAP在多个OKS（0.5:0.05:0.95）上的平均作为我们最主要的衡量指标。此外，我们将CrowdPose按照CI分为：easy (0-0.1)，medium (0.1-0.8)，hard (0.8-1)，来更好的评估我们在不同场景下的表现。我们在所有实验中采用了和COCO相同的标准来计算OKS。

5.2. 评价指标

我们采用MSCOCO的评价指标，使用平均精度(AP)和平均召回率(AR)来评价结果。对象关键点相似度(OKS)与IoU作用相同，采用AP/AR进行关键点检测。我们将多个OKS值(.50:.05:.95)上的mAP作为我们的主要度量。此外，为了更好地评估我们的模型在不同拥挤场景下的性能，我们将CrowdPose数据集根据CrowdIndex划分为三个拥挤级别：容易(0-0.1)、中等(0.1-0.8)和困难(0.81)。当在所有实验中计算OKS时，我们使用与MSCOCO相同的关键点标准差。

5.3. 实验细节

我们的方法采用了自上而下的框架。由于检测和姿态估计网络不是我们的关注重点，我们采用了YoloV3 [24]和AlphaPose [13]这两个SOTA检测器作为我们的目标和关键点检测器。在训练过程中我们采用了旋转（ $\pm 30^{\circ }$ ）和缩放（ $\pm 30\%$ ）和翻转的数据增强技术。输入的分辨率为 $320\times 256$ ，输出分辨率为 $80\times 64$ 。最后学习率设为 $1\times 10^{-4}$ 并在80个epoch后衰减为 $1\times 10^{-5}$ 。Mini-batch size为64并采用了RMSprop [28]优化器。在训练过程中，我们首先对检测框在宽高方向上扩展30%，然后再通过我们的JC SPPE网络。JC的位置通过对输出的HM在原始和翻转后的图片上进行平均。我们在两块Nvidia 1080Ti GPUs上进行我们的实验。我们采用PyTorch来实现我们的框架

为了和现有的SOTA [14, 32, 13]在CrowdPose数据集上进行比较，我们根据作者提供的配置信息进行了重训。为了公平起见，我们统一采用了ResNet101作为所有SPPE网络的主干。对于Mask-R-CNN我们同样使用了基于FPN的ResNet主干网络，相同的训练batch size。

5.4. 结果

CrowdPose: 定量的结果如表1所示。我们的方法比现有的SOTA方法要高5.2 mAP。这证明了我们提出的方法在解决密集人群姿态估计中的有效性。为了更好的研究我们的方法，我们在表2中呈现了在三种不同CI的图片上的结果。需要注意的是，我们在稀疏人群上提高了4.1 mAP，中等密集人群上提高了4.9以及高密集人群上提高了6.2 mAP。这更加证明了我们方法在密集人群上的有效性。我们把定性的结果呈现在图7中。其他的结果请参见附件。


MSCOCO: 我们同样在MSCOCO数据集上评估了我们的结果，如表3所示。在不使用任何特殊技巧的前提下，我们达到了70.9 mAP。这相比较现有的AlphaPose提高了0.8，在使用相同的检测器和SPPE网络的情况下。这说明了我们在姿态估计问题上泛用能力。注意对于[32]，他们文章中提到的最强的行人检测器并没有开源。为了公平的比较，我们采用了YoloV3作为行人检测器。

Inference Speed: 现有完全开源的方法的运行速度结果如图2所示。我们在测试集上的运行速度平均得到我们的运行速度。为了得到最好的结果，我们使用了最精确的OpenPose[5]的配置结果，输入是 $1024\times 736$ 。如表所示，我们的方法达到了10.1 FPS，这紧紧闭AlphaPose要慢一点点而比其他的方法都要快很多。

5.5 消融实验

我们研究了不同模块对于我们提出的方法的影响，如表4所示。

Joints Candidate Loss: 我们首先评估了我们JC loss的有效性。实验中，我们将JC loss替换为在姿态估计中广泛使用的传统的MSE loss。实验结果如表4(a)所示。最终的mAP要下降4.3%。这表明我们的损失函数能够 鼓励SPPE来预测更多的JC并保留尽可能多的结果。

Globally Optimizing Association: 然后我们比较了几种NMS算法，包括bounding box NMS、pose-NMS [3, 7]和参数化 pose-NMS。试验结果如表4(b)所示。我们可以发现我们的方法极大的提高了最终模型的精度。需要注意的是，这些NMS 算法都是基于实例的，它们会在实例层面消除重复。而实例层面的结果并不能很好的解决姿态估计问题。由于行人姿态的复杂性，我们需要在JC层面来消除重复。同时，所有的NMS方法本质上都是贪婪算法，所以它们的结果往往并不是全局最优。我们的匹配算法可以在全局给出最优结果，并保持计算效率。

6. 总结

在这篇文章中，我们提出了一种全新的方法来解决遮挡问题。通过SPPE输出的JC HM，建立行人-关节图模型，我们把姿态估计问题变成了一个全局最优化匹配问题。为了更好的验证我们的方法在密集人群上的表现，我们建立了CrowdPose数据集，它的CI在[0, 1]间服从一个均匀分布。我们提出的方法在CrowdPose数据集上显著的超过了其他现有SOTA方法。在MSCOCO数据集上的结果，显示了我们的方法具有很好的泛化能力。